Sage 9.4 Release Tour

released Aug 22, 2021

Contents

  1. Sage 9.4 Release Tour
    1. Symbolics
      1. Extended interface with SymPy
      2. ConditionSet
      3. symbolic_expression(lambda x, y: ...)
    2. Convex geometry
      1. ABC for convex sets
      2. New operations on faces of convex polyhedra
      3. Parallel face iterator
      4. Polyhedral complexes
      5. More details
    3. Knot theory
      1. Databases
      2. Testing isotopy
    4. Manifolds
      1. Unicode characters for various symbols in plain text outputs
      2. Specifying coordinate restrictions while declaring a new chart
      3. Defining submanifolds and manifold subsets by pullbacks from Sage sets
      4. Manifold options for RealSet constructors
      5. Families and posets of manifold subsets
      6. New method for constructing a tangent vector
      7. De Rham cohomology
      8. Internal code improvements and bug fixes
    5. Coding theory
      1. AG codes
    6. Algebra
      1. New algebraic objects
      2. Bug fixes and improvements
    7. Hyperbolic geometry
    8. Configuration changes
      1. Support for system gcc/g++/gfortran 11 added
      2. Support for system Python 3.6 dropped
      3. Support for optional packages on systems with gcc 4.x dropped
      4. For developers: ./configure --prefix=SAGE_LOCAL --with-sage-venv=SAGE_VENV
    9. Package upgrades
      1. FLINT and Arb
      2. NumPy and SciPy
      3. lrslib and polymake
      4. PARI/GP and GAP
      5. Maxima and FriCAS
      6. Other upgrades
    10. For developers and packagers: Refactoring, modernization, and modularization
      1. Using type annotations (PEP 563) in the Sage library
      2. New location for distribution package sources: SAGE_ROOT/pkgs
      3. Modern Python packaging metadata for sagemath-standard
      4. Using cython.parallel in sage
    11. Availability of Sage 9.4 and installation help
      1. Sources
      2. Installation FAQ
      3. Availability as binaries and in distributions
      4. Alternative installation methods using pip
      5. pip-installable subset distributions
    12. More details

Symbolics

Extended interface with SymPy

The SymPy package has been updated to version 1.8.

SageMath has a bidirectional interface with SymPy. Symbolic expressions in Sage provide a _sympy_ method, which converts to SymPy; also, Sage attaches _sage_ methods to various SymPy classes, which provide the opposite conversion.

In Sage 9.4, several conversions have been added. Now there is a bidirectional interface as well for matrices and vectors. #31942 

sage: M = matrix([[sin(x), cos(x)], [-cos(x), sin(x)]]); M
[ sin(x)  cos(x)]
[-cos(x)  sin(x)]
sage: sM = M._sympy_(); sM
Matrix([
[ sin(x), cos(x)],
[-cos(x), sin(x)]])
sage: sM.subs(x, pi/4)           # computation in SymPy
Matrix([
[ sqrt(2)/2, sqrt(2)/2],
[-sqrt(2)/2, sqrt(2)/2]])

Work is underway to make SymPy's symbolic linear algebra methods available in Sage via this route.

Callable symbolic expressions, such as those created using the Sage preparser's f(...) = ... syntax, now convert to a SymPy Lambda. #32130 

sage: f(x, y) = x^2 + y^2; f
(x, y) |--> x^2 + y^2
sage: f._sympy_()
Lambda((x, y), x**2 + y**2)

Sage has added a formal set membership function element_of for use in symbolic expressions; it converts to a SymPy's Contains expression. #24171

Moreover, all sets and algebraic structures (Parents) of SageMath are now accessible to SymPy by way of a wrapper class SageSet, which implements the SymPy Set API. #31938 

sage: F = Family([2, 3, 5, 7]); F
Family (2, 3, 5, 7)
sage: sF = F._sympy_(); sF
SageSet(Family (2, 3, 5, 7))          # this is how the wrapper prints
sage: sF._sage_() is F
True                                  # bidirectional
sage: bool(sF)
True
sage: len(sF)
4
sage: sF.is_finite_set                # SymPy property
True

Finite or infinite, we can wrap it: 

sage: W = WeylGroup(["A",1,1])
sage: sW = W._sympy_(); sW
SageSet(Weyl Group of type ['A', 1, 1] (as a matrix group acting on the root space))
sage: sW.is_finite_set
False
sage: sW.is_iterable
True
sage: sB3 = WeylGroup(["B", 3])._sympy_(); sB3
SageSet(Weyl Group of type ['B', 3] (as a matrix group acting on the ambient space))
sage: len(sB3)
48

Some parents or constructions have a more specific conversion to SymPy. #31931, #32015 

sage: ZZ3 = cartesian_product([ZZ, ZZ, ZZ])
sage: sZZ3 = ZZ3._sympy_(); sZZ3
ProductSet(Integers, Integers, Integers)
sage: (1, 2, 3) in sZZ3

sage: NN = NonNegativeIntegers()
sage: NN._sympy_()
Naturals0

sage: (RealSet(1, 2).union(RealSet.closed(3, 4)))._sympy_()
Union(Interval.open(1, 2), Interval(3, 4))

sage: X = Set(QQ).difference(Set(ZZ)); X
Set-theoretic difference of
 Set of elements of Rational Field and
 Set of elements of Integer Ring
sage: X._sympy_()
Complement(Rationals, Integers)

sage: X = Set(ZZ).difference(Set(QQ)); X
Set-theoretic difference of
 Set of elements of Integer Ring and
 Set of elements of Rational Field
sage: X._sympy_()
EmptySet

See Meta-ticket #31926: Connect Sage sets to SymPy sets

ConditionSet

Sage 9.4 introduces a class ConditionSet for subsets of a parent (or another set) consisting of elements that satisfy the logical "and" of finitely many predicates. #32089 

sage: in_small_oblong(x, y) = x^2 + 3 * y^2 <= 42
sage: SmallOblongUniverse = ConditionSet(QQ^2, in_small_oblong)
sage: SmallOblongUniverse
{ (x, y) ∈ Vector space of dimension 2 over Rational Field : x^2 + 3*y^2 <= 42 }

sage: parity_check(x, y) = abs(sin(pi/2*(x + y))) < 1/1000
sage: EvenUniverse = ConditionSet(ZZ^2, parity_check); EvenUniverse
{ (x, y) ∈ Ambient free module of rank 2 over the principal ideal
           domain Integer Ring : abs(sin(1/2*pi*x + 1/2*pi*y)) < (1/1000) }

sage: SmallOblongUniverse & EvenUniverse
{ (x, y) ∈ Free module of degree 2 and rank 2 over Integer Ring
Echelon basis matrix:
[1 0]
[0 1] : x^2 + 3*y^2 <= 42, abs(sin(1/2*pi*x + 1/2*pi*y)) < (1/1000) }

The name ConditionSet is borrowed from SymPy. In fact, if the given predicates (condition) are symbolic, a ConditionSet can be converted to a SymPy ConditionSet; the _sympy_ method falls back to creating a SageSet wrapper otherwise.

symbolic_expression(lambda x, y: ...)

Sage 9.4 has added a new way to create callable symbolic expressions. #32103

The global function symbolic_expression now accepts a callable such as those created by lambda expressions. The result is a callable symbolic expression, in which the formal arguments of the callable are the symbolic arguments.

Example: 

symbolic_expression(lambda x,y: x^2+y^2) == (SR.var("x")^2 + SR.var("y")^2).function(SR.var("x"), SR.var("y"))

This provides a convenient syntax in particular in connection to ConditionSet.

Instead of 

sage: predicate(x, y, z) = sqrt(x^2 + y^2 + z^2) < 12  # preparser syntax, creates globals
sage: ConditionSet(ZZ^3, predicate)

one is now able to write 

sage: ConditionSet(ZZ^3, symbolic_expression(lambda x, y, z: 
....:     sqrt(x^2 + y^2 + z^2) < 12))

Convex geometry

ABC for convex sets

Sage 9.4 has added an abstract base class ConvexSet_base (as well as abstract subclasses ConvexSet_closed, ConvexSet_compact, ConvexSet_relatively_open, ConvexSet_open) for convex subsets of finite-dimensional real vector spaces. The abstract methods and default implementations of methods provide a unifying API to the existing classes Polyhedron_base, ConvexRationalPolyhedralCone, LatticePolytope, and PolyhedronFace. #31919, #31959, #31990, #31993

Several methods previously only available for Polyhedron_base instances, are now available for all convex sets. The method an_affine_basis returns a sequence of points that span by affine linear combinations the affine hull, i.e., the smallest affine subspace in which the convex set lies. The method affine_hull returns the latter as a polyhedron. The method affine_hull_projection (renamed from affine_hull in Sage 9.1) computes an affine linear transformation of the convex set to a new ambient vector space, in which the image is full-dimensional. The generalized method also provides additional data: the right inverse (section map) of the projection. #27366, #31963, #31993

As part of the ConvexSet_base API, there are new methods for point-set topology such as is_open, relative_interior, and closure. For example, taking the relative_interior of a polyhedron constructs an instance of RelativeInterior, a simple object that provides a __contains__ method and all other methods of the ConvexSet_base API. #31916 

sage: P = Polyhedron(vertices=[(1,0), (-1,0)])
sage: ri_P = P.relative_interior(); ri_P
Relative interior of
 a 1-dimensional polyhedron in ZZ^2 defined as the convex hull of 2 vertices
sage: (0, 0) in ri_P
True
sage: (1, 0) in ri_P
False

ConvexSet_base is a subclass of the new abstract base class Set_base. #32013

This makes various methods that were previously only defined for sets constructed using the Set constructor available for polyhedra and other convex sets. As an example, we can now do: 

sage: polytopes.cube().union(polytopes.tetrahedron())                                                                                                                                                
Set-theoretic union of 
 Set of elements of A 3-dimensional polyhedron in ZZ^3 defined as the convex hull of 8 vertices and 
 Set of elements of A 3-dimensional polyhedron in ZZ^3 defined as the convex hull of 4 vertices

New operations on faces of convex polyhedra

PolyhedronFace has a new method affine_tangent_cone. #29811 

sage: c = polytopes.cube()
sage: edge = min(c.faces(1))
sage: edge.vertices()
(A vertex at (1, -1, -1), A vertex at (1, 1, -1))
sage: T_edge = edge.affine_tangent_cone()
sage: T_edge.Vrepresentation()
(A line in the direction (0, 1, 0),
 A ray in the direction (0, 0, 1),
 A vertex at (1, 0, -1),
 A ray in the direction (-1, 0, 0))

Sage 9.4 also defines two new Polyhedron_base methods that look up a face in the face lattice of a polyhedron. #29683

Parallel face iterator

The f-vector of polyhedra is now computed in parallel on many platforms.

For developers: This is done with a parallel face iterator. Instead of just counting the faces, one can also perform different operations in parallel.

Polyhedral complexes

Sage 9.4 defines a new subclass of GenericCellComplex for (geometric) polyhedral complexes, PolyhedralComplex #31748 

sage: pc = PolyhedralComplex([
....:         Polyhedron(vertices=[(1/3, 1/3), (0, 0), (1/7, 2/7)]),
....:         Polyhedron(vertices=[(1/7, 2/7), (0, 0), (0, 1/4)])])
sage: [p.Vrepresentation() for p in pc.cells_sorted()]
[(A vertex at (0, 0), A vertex at (0, 1/4), A vertex at (1/7, 2/7)),
 (A vertex at (0, 0), A vertex at (1/3, 1/3), A vertex at (1/7, 2/7)),
 (A vertex at (0, 0), A vertex at (0, 1/4)),
 ...
 (A vertex at (1/7, 2/7),),
 (A vertex at (1/3, 1/3),)]
sage: pc.plot()
Graphics object consisting of 10 graphics primitives
sage: pc.is_pure()
True
sage: pc.is_full_dimensional()
True
sage: pc.is_compact()
True
sage: pc.boundary_subcomplex()
Polyhedral complex with 4 maximal cells
sage: pc.is_convex()
True
sage: pc.union_as_polyhedron().Hrepresentation()
(An inequality (1, -4) x + 1 >= 0,
 An inequality (-1, 1) x + 0 >= 0,
 An inequality (1, 0) x + 0 >= 0)
sage: pc.face_poset()
Finite poset containing 11 elements
sage: pc.is_connected()
True
sage: pc.connected_component() == pc
True

The homogeneous analogue to a polyhedral complex is a polyhedral fan. The constructor Fan for instances of the class RationalPolyhedralFan has been generalized: If the new keyword allow_arrangement=True is passed, the input is allowed to be an arbitrary finite set (arrangement) of rational polyhedral cones; Sage then computes a suitable common refinement that is a fan. #25122

More details

Some smaller improvements that are listed in the release notes for optimization and polyhedral geometry software interactions in Sage.

Knot theory

Databases

A direct access to the contents of the KnotInfo and LinkInfo databases is available as an optional Sage package, now (see Trac #30352). It can be installed via 

sage -i database_knotinfo

For example, you can obtain the Kauffman polynomial of a link via these databases which has no implementation in Sage, so far: 

sage: B = BraidGroup(8)
sage: L = Link(B([-1, -1, -1, -2, 1, -2, 3, -2, 3]))
sage: K, mirrored  = L.get_knotinfo(); K, mirrored
(<KnotInfo.K8_14: '8_14'>, True)
sage: K.kauffman_polynomial()
z^4 + 2*a^-1*z^5 + 2*a^-2*z^6 + a^-3*z^7 - 2*z^2 - 3*a^-1*z^3 - a^-2*z^4 + 3*a^-3*z^5
 + 5*a^-4*z^6 + a^-5*z^7 + 1 + a^-1*z - a^-2*z^2 - 6*a^-3*z^3 - 7*a^-4*z^4 + 4*a^-5*z^5
 + 3*a^-6*z^6 + 3*a^-3*z + 3*a^-4*z^2 - 8*a^-5*z^3 - 4*a^-6*z^4 + 3*a^-7*z^5 + 3*a^-5*z
 + a^-6*z^2 - 5*a^-7*z^3 + a^-8*z^4 + a^-7*z - a^-8*z^2

Testing isotopy

There is a new method is_isotopic which allows to check if two links are isotopic to each other: 

sage: l1 = Link([[2, 9, 3, 10], [4, 13, 5, 14], [6, 11, 7, 12],
....:            [8, 1, 9, 2], [10, 7, 11, 8], [12, 5, 13, 6],
....:            [14, 3, 1, 4]])
sage: l2 = Link([[1, 8, 2, 9], [9, 2, 10, 3], [3, 14, 4, 1],
....:            [13, 4, 14, 5], [5, 12, 6, 13], [11, 6, 12, 7],
....:            [7, 10, 8, 11]])
sage: l1 == l2
False
sage: l1.is_isotopic(l2)
True
sage: l3 = l2.mirror_image()
sage: l1.is_isotopic(l3)
False

Manifolds

The full list of changes is available in this changelog.

Unicode characters for various symbols in plain text outputs

In plain text mode, various symbols are now displayed by means of Unicode characters instead of ASCII workarounds (#30473). This regards

Specifying coordinate restrictions while declaring a new chart

The manifold method chart has been endowed with the new argument coord_restrictions, allowing to define conditions restricting the range of coordinates (#32102). For instance to define a half disk above the diagonal x+y=0: 

sage: M = Manifold(2, 'M')                                                                         
sage: X.<x,y> = M.chart(coord_restrictions=lambda x,y: [x^2+y^2<1, x+y>0]) 
sage: X.plot(max_range=1, number_values=41)

slanted_half_disk.png

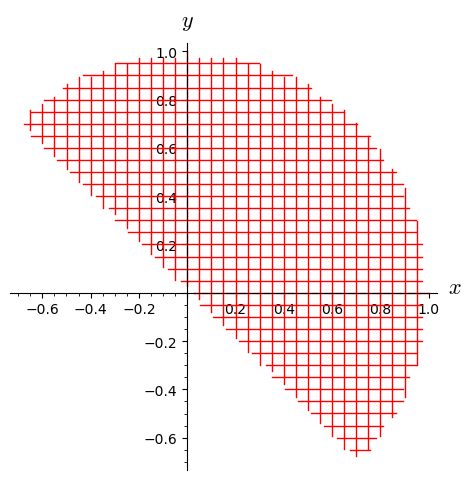
Previously, to achieve the same result, one had to invoke X.add_restrictions([x^2+y^2<1, x+y>0]) after the declaration of the chart X. The method add_restrictions is now deprecated.

Defining submanifolds and manifold subsets by pullbacks from Sage sets

Given a continuous map Φ from a topological or differentiable manifold N and a subset S of the codomain of Φ, we define the pullback (preimage) of S as the subset of N of points p with Φ(p) in S. #31688

Generically, such pullbacks are represented by instances of the new class ManifoldSubsetPullback. But because Φ is continuous, topological closures and interiors pull back accordingly. Hence, in some cases we are able to give the pullback additional structure, such as creating a submanifold rather than merely a manifold subset.

In addition to the case when Φ is a continuous map between manifolds, there are two situations that connect Sage manifolds to sets defined by other components of Sage:

In a similar direction, the new method ConvexSet_base.affine_hull_manifold makes the affine hull of a convex set available as a Riemannian submanifold embedded into the ambient Euclidean space. #31659

Manifold options for RealSet constructors

As an application of chart pullbacks, the RealSet constructors have been extended so that they can optionally build manifolds or manifolds subsets. #31881

This is activated by passing the manifold keyword structure='differentiable': 

sage: RealSet(-oo, oo, structure='differentiable')
Real number line ℝ

sage: RealSet([0, 1], structure='differentiable')
Subset [0, 1] of the Real number line ℝ

It is also implied when a coordinate name is given using the keyword coordinate: 

sage: RealSet(0, 1, coordinate='λ')
Open subset (0, 1) of the Real number line ℝ
sage: _.category()
Join of
 Category of smooth manifolds over Real Field with 53 bits of precision and
 Category of connected manifolds over Real Field with 53 bits of precision and
 Category of subobjects of sets

It is also implied by assigning a coordinate name using generator notation: 

sage: R_xi.<ξ> = RealSet.real_line(); R_xi
Real number line ℝ
sage: R_xi.canonical_chart()
Chart (ℝ, (ξ,))

The above example showed the use of the new constructor RealSet.real_line. The manifold keywords work for all other specialized constructors for various types of intervals, as well.

Constructor

Interval

RealSet.open

(a, b)

RealSet.closed

[a, b]

RealSet.point

{a}

RealSet.open_closed

(a, b]

RealSet.closed_open

[a, b)

RealSet.unbounded_below_closed

(-oo, b]

RealSet.unbounded_below_open

(-oo, b)

RealSet.unbounded_above_closed

[a, +oo)

RealSet.unbounded_above_open

(a, +oo)

RealSet.real_line

(-oo, +oo)

new in Sage 9.4

RealSet.interval

any

new in Sage 9.4

The global bindings RealLine and OpenInterval, which create manifolds, are now deprecated, but these constructors will remain available through the manifolds catalog, via manifolds.RealLine and manifolds.OpenInterval. The objects made by these constructors are now also valid input for RealSet. #30832

Families and posets of manifold subsets

In Sage 9.4, the system for declaring (named) subsets of topological and differentiable manifolds has become more general and powerful.

In addition to declare_union and declare_intersection, there are now methods declare_empty, declare_nonempty, declare_subset, declare_superset, and declare_equal.

The declared subset relations define a quasiorder on the named subsets. To visualize the subset relations, methods subset_digraph and superset_digraph are now available.

Through a sequence of subset declarations, or directly through declare_equal, several named subsets (which are distinct as Python objects) can become necessarily equal as mathematical sets. By quotienting out by this equivalence relation, we obtain a partially ordered set, which is available through the new methods subset_poset and superset_poset.

The new class ManifoldSubsetFiniteFamily serves as a container for storing arbitrary finite families of manifold subsets, indexed by their names. The new methods subset_family, superset_family, and open_superset_family return instances of ManifoldSubsetFiniteFamily. Such instances are automatically sorted by name, are hashable, compare with each other lexicographically, and print more compactly than lists/tuples/sets of manifold subsets.

For more information, see Meta-ticket #31740.

New method for constructing a tangent vector

Manifolds have been endowed with the method tangent_vector (shortcut alias vector) for the direct construction of a tangent vector at a given point (#31609): 

sage: M = Manifold(2, 'M')                                                                          
sage: X.<x,y> = M.chart()                                                                           
sage: p = M((1, 2), name='p')                                                                       
sage: v = M.tangent_vector(p, -1, 3); v                                                             
Tangent vector at Point p on the 2-dimensional differentiable manifold M
sage: v.display()                                                                                   
-∂/∂x + 3 ∂/∂y

Previously, tangent vectors could only be constructed as elements of the tangent space at the given point: 

sage: Tp = M.tangent_space(p)                                                                       
sage: v = Tp((-1, 3))

De Rham cohomology

De Rham cohomology has been implemented via the new classes DeRhamCohomologyRing and DeRhamCohomologyClass; the algebra of mixed differential forms has been turned into a de Rham complex (#31691)

Internal code improvements and bug fixes

Various improvements/refactoring of the code have been performed in this release:

In addition, various bugs have been fixed: #31784, #31904, #31923, #32112.

Coding theory

AG codes

Algebraic geometry codes (shortly AG codes) and their decoders are now available in Sage 9.4 (see #27957).

It is first time that all AG codes as originally defined by Goppa in 1981 are equipped with an efficient decoding algorithm implemented in free software. This has become possible when global function fields machinery was implemented in Sage 8. Most famous error correcting codes such as Reed-Solomon codes and Goppa codes (the workhorse of the McEliece cryptosystem which is a candidate of the NIST standardization process for post-quantum cryptography) are special cases of AG codes.

A user should be warned that creating a decoder for a long AG code may take a long time, but decoding with the created decoder should be quick. 

sage: F.<a> = GF(64)
sage: A1 = AffineSpace(F,1)
sage: C = Curve(A1)
sage: C
Affine Line over Finite Field in a of size 2^6
sage: pls = C.places()
sage: Q, = C.places_at_infinity()
sage: pls.remove(Q)
sage: code = codes.EvaluationAGCode(pls, 31*Q)  # creating a Reed-Solomon code; be patient
sage: code
[64, 32] evaluation AG code over GF(64)
sage: decoder = code.decoder('K')               # be patient once more
sage: tau = decoder.decoding_radius()
sage: tau
16
sage: channel = channels.StaticErrorRateChannel(code.ambient_space(), tau)  # let's try decoding
sage: message_space = decoder.message_space()
sage: encoder = decoder.connected_encoder()
sage: message = message_space.random_element()  # a random message
sage: codeword = encoder.encode(message)        # codeword encoding the message
sage: received_vector = channel(codeword)       # codeword sent through the noisy channel
sage: (received_vector - codeword).hamming_weight()
16
sage: decoder.decode_to_code(received_vector) == codeword    # recovered the codeword
True
sage: decoder.decode_to_message(received_vector) == message  # recovered the message
True

Algebra

New algebraic objects

Bug fixes and improvements

Hyperbolic geometry

Bug fixed with computing the Möbius transform, midpoint, and perpendicular bisector in the hyperbolic plane. Now the computation of midpoint and perp. bisector is order independent. #29936

Configuration changes

Support for system gcc/g++/gfortran 11 added

Sage can now be built using GCC 11. #31786

This enables building Sage using the default compiler on Fedora 34, and on macOS with homebrew using the default compilers. (Previously, in Sage 9.3, specific older versions of the compilers had to be installed.)

Support for system Python 3.6 dropped

It was already deprecated in Sage 9.3. #30551

It is still possible to build the Sage distribution on systems with old Python versions, but Sage will build its own copy of Python 3.9.x in this case.

Support for optional packages on systems with gcc 4.x dropped

Sage is phasing out its support for building from source using very old compilers from the gcc 4.x series.

As of Sage 9.4, on systems such as ubuntu-trusty (Ubuntu 14.04), debian-jessie (8), linuxmint-17, and centos-7 that only provide gcc from the outdated 4.x series, it is still supported to build Sage from source with the system compilers. However, building optional and experimental packages is no longer supported, and we have removed these configurations from our CI. #31526

Users in scientific computing environments using these platforms should urge their system administrators to upgrade to a newer distribution, or at least to a newer toolchain.

For developers: ./configure --prefix=SAGE_LOCAL --with-sage-venv=SAGE_VENV

Sage 9.4 makes it possible to configure the build to make a distinction between:

Package installation records are kept within each tree, and thus separately. This allows developers to switch between different system Python versions without having to rebuild the whole set of non-Python packages. See #29013 for details.

Package upgrades

FLINT and Arb

FLINT has been upgraded to 2.7.1 in #31069. Sage 9.4 has added support for using FLINT 2.8.x on systems that provide it in #32175. The minimum supported FLINT version is now 2.6.0 #31525. Sage developers can now make use of more FLINT features added in the 2.x development series, see Meta-ticket #31408: Use new features from FLINT 2.x.

Arb has been upgraded to 2.19.0, which brings various performance improvements.

NumPy and SciPy

Many upgrades were enabled by dropping support for Python 3.6.

In particular, NumPy has been upgraded to 1.20.3 in #31008. Sage users benefit from many improvements made in the NumPy 1.20 series. The minimum version of NumPy supported by the Sage library, according to build/pkgs/numpy/install-requires.txt, is still 1.19 (slightly ahead of the NEP 29 drop schedule).

SciPy has been upgraded to 1.6.3 in #31008; the minimum version supported by the Sage library, according to build/pkgs/scipy/install-requires.txt, is still 1.5. The SciPy 1.6 series has brought many improvements. Among the many highlights, the integration of the high-performance linear programming library HiGHS stands out. #32282 tracks the task of making use of it as a backend of MixedIntegerLinearProgram in Sage.

lrslib and polymake

lrslib, providing reverse search algorithms for vertex enumeration for polyhedra and equilibrium problems, has been upgraded to version 071b, which promises major speedups thanks to a new hybrid arithmetic. #27745

polymake, a powerful system for computations with convex polyhedra, simplicial complexes, matroids, graphs, and tropical hypersurfaces, has been upgraded to version 4.4 in #27745. The major upgrade from version 3.4 has brought many improvements made during the polymake 3.5, 3.6, 4.0, 4.1, 4.2, 4.3, and 4.4 development cycles. To use polymake from Sage, use sage -i jupymake, which activates a more robust interface; the original pexpect-based interface is now deprecated. Sage 9.4 also contains a number of interface and packaging improvements for polymake. #26368, #31864, #31840

PARI/GP and GAP

PARI/GP, the computer algebra system designed for fast computations in number theory, has been upgraded to 2.13.1 in #30801. The upgrade from version 2.11.4 has brought many improvements.

GAP, the system for computational group theory and other discrete algebra, has been upgraded to 4.11.1. Although considered by upstream as a minor update from version 4.11.0, which was included in Sage 9.3, it provides many improvements and updates to GAP packages.

Maxima and FriCAS

The symbolics packages Maxima and FriCAS, both running on Embeddable Common Lisp (ECL), have been upgraded to 5.45.0 and 1.3.7, respectively.

Also, if ECL 21.2.1 is provided by a system package, Sage is now able to use it instead of building its own copy. #29617

Other upgrades

For developers and packagers: Refactoring, modernization, and modularization

Using type annotations (PEP 563) in the Sage library

Dropping support for Python 3.6 has allowed us to start using language and library features introduced in Python 3.7. Meta-ticket #29756 tracks such features by Python version.

One notable new feature of Python 3.7 is type annotations for function arguments and return values. Sage 9.4 has started to make use of this feature, in the revised form that PEP 563 provides (from __future__ import annotations). A new section in the developer's manual added in #32067 provides guidance on how to use this feature. See #32058, #32128, #32164 for examples.

New location for distribution package sources: SAGE_ROOT/pkgs

The Sage source tree contains a number of source trees of Python distribution packages. In Sage 9.4, they have been moved to a new central location. #31577 

SAGE_ROOT
- pkgs
  - sage-conf
    - setup.py
    - bin/
    - sage_conf.py.in
  - sage-docbuild
    - setup.py
    - sage_docbuild   -> symlinks to SAGE_ROOT/sage_docbuild/
  - sage-sws2rst
    - setup.py
    - bin/
    - sage_sws2rst/
  - sagemath-standard
    - setup.py
    - bin             -> symlinks to SAGE_ROOT/src/bin/        
    - sage            -> symlinks to SAGE_ROOT/src/sage/
    - sage_setup      -> symlinks to SAGE_ROOT/src/sage_setup/

that is, the new directory pkgs is on the same level as 

SAGE_ROOT
- src

the unchanged monolithic sagelib source tree, which will continue to contain subdirectories 

  - bin/ 
  - doc/
  - sage/
  - sage_docbuild/      # was sage_setup/docbuild/ in Sage 9.2
  - sage_setup/

All files that contain Sage doctests (tested with sage -t or make ptest) remain in the monolithic src/ source tree; the source trees of the distributions symlink there.

Other modularization tickets will add 

SAGE_ROOT
- pkgs
  - sagemath-core/
  - sagemath-brial/
  - sagemath-giac/
  - sagemath-meataxe/
  - sagemath-tdlib/

etc.; see Meta-ticket #29705 for more information.

Modern Python packaging metadata for sagemath-standard

./bootstrap now generates modern Python packaging metadata (pyproject.toml and setup.cfg, as well as requirements.txt and Pipfile) for our distribution package sagemath-standard. #30913

The version information for dependencies comes from the existing files build/pkgs/*/install-requires.txt.

Using cython.parallel in sage

One can now use cython.parallel for parallel cython code, as demonstrated in #31245.

The following cython code will work (in a source file and compiled in the shell): 

# distutils: extra_compile_args = OPENMP_CFLAGS
# distutils: extra_link_args = OPENMP_CFLAGS

from cython.parallel cimport prange, threadid

def foo():
    cdef int i, sum
    sum = 0
    for i in prange(1000, num_threads=8, schedule='dynamic', nogil=True):
        sum += threadid()
    return sum

OPENMP_CFLAGS and OPENMP_CXXFLAGS will be configured non-empty on many systems, if OpenMP is detected and working. If empty, the above code will still compile fine and run on only 1 thread instead. In particular one needs to use cython.parallel functions and not call OpenMP directly, e.g. with omp_get_thread_num.

Availability of Sage 9.4 and installation help

Sage 9.4 was released on 2021-08-22.

Sources

The Sage source code is available in the sage git repository, and the self-contained source tarballs are available for download.

SageMath 9.4 supports most platforms that were supported by Sage 9.3. Sage 9.4 now has support for building Sage from source on macOS 11 ("Big Sur") with the default compilers from Xcode; and the default compilers from homebrew. Our CI now tests also several flavors of openSUSE Linux.

Sage 9.4 has been tested to compile from source on a wide variety of platforms, including:

There are currently known issues with an installation from source on conda-forge, both on Linux and macOS. This is tracked in #32087.

Installation FAQ

See README.md in the source distribution for installation instructions.

See sage-release, sage-devel.

Availability as binaries and in distributions

The easiest way to install Sage 9.4 is through a distribution that provides it, see repology.org: sagemath.

A binary build of Sage 9.4 for macOS as a signed and notarized app is available.

Binaries for Linux platforms are available.

Note also that the binary packages do not support installing optional Sage packages. If you need any of these packages, install Sage from source instead, see above.

Sage 9.4 is available on the CoCalc.com online workspace; however, the CoCalc docker image is still using Sage 9.3.

Alternative installation methods using pip

Since Sage 9.3, installation methods using pip are available. 

   $ python3 -m pip install sage_conf

This will download the distribution package (sdist) sage_conf from PyPI, which will build the non-Python components of the Sage distribution in a subdirectory of $HOME/.sage.

After installation of sage_conf, a wheelhouse containing wheels of various Python packages is available; type ls $(sage-config SAGE_SPKG_WHEELS) to list them and python3 -m pip install $(sage-config SAGE_SPKG_WHEELS)/*.whl to install them.

After this, you can install the Sage library, using any of these options:

pip-installable subset distributions

Two new, experimental distribution packages are available on PyPI: #29865

More details