|
Size: 2187
Comment: Summarize #6272, #6271; reminders to showcase features
|
Size: 9524
Comment: Summarize #6014, #6051, #6185, #5975
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 11: | Line 11: |
| * FIXME: summarize #5845 * FIXME: summarize #6229 * FIXME: summarize #6250 |
* Correct precision bound in {{{hilbert_class_polynomial()}}} and miscellaneous new functions (John Cremona) -- The two new functions are {{{elliptic_j()}}} in {{{sage/functions/special.py}}}, and {{{is_primitive()}}} in the class {{{BinaryQF}}} of {{{sage/quadratic_forms/binary_qf.py}}}. The function {{{elliptic_j(z)}}} returns the elliptic modular {{{j}}}-function evaluated at {{{z}}}. The function {{{is_primitive()}}} determines whether the binary quadratic form {{{ax^2 + bxy + cy^2}}} satisfies {{{gcd(a,b,c) = 1}}}, i.e. that it is primitive. Here are some examples on using these new functions: {{{ sage: elliptic_j(CC(i)) 1728.00000000000 sage: elliptic_j(sqrt(-2.0)) 8000.00000000000 sage: Q = BinaryQF([6,3,9]) sage: Q.is_primitive() False sage: Q = BinaryQF([1,1,1]) sage: Q.is_primitive() True }}} * Efficient Lagrange interpolation polynomial (Yann Laigle-Chapuy) -- Calculating the Lagrange interpolation polynomial of a set of points is now up to 48% faster than previously. The following timing statistics were obtained using the machine sage.math: {{{ # BEFORE sage: R = PolynomialRing(QQ, 'x') sage: %timeit R.lagrange_polynomial([(0,1),(2,2),(3,-2),(-4,9)]) 1000 loops, best of 3: 824 µs per loop sage: R.lagrange_polynomial([(0,1),(2,2),(3,-2),(-4,9)]) -23/84*x^3 - 11/84*x^2 + 13/7*x + 1 sage: R = PolynomialRing(GF(2**3,'a'), 'x') sage: a = R.base_ring().gen() sage: timeit("R.lagrange_polynomial([(a^2+a,a),(a,1),(a^2,a^2+a+1)])") 625 loops, best of 3: 111 µs per loop sage: R.lagrange_polynomial([(a^2+a,a),(a,1),(a^2,a^2+a+1)]) a^2*x^2 + a^2*x + a^2 # AFTER sage: R = PolynomialRing(QQ, 'x') sage: %timeit R.lagrange_polynomial([(0,1),(2,2),(3,-2),(-4,9)]) 1000 loops, best of 3: 425 µs per loop sage: R.lagrange_polynomial([(0,1),(2,2),(3,-2),(-4,9)]) -23/84*x^3 - 11/84*x^2 + 13/7*x + 1 sage: R = PolynomialRing(GF(2**3,'a'), 'x') sage: a = R.base_ring().gen() sage: timeit("R.lagrange_polynomial([(a^2+a,a),(a,1),(a^2,a^2+a+1)])") 625 loops, best of 3: 86.4 µs per loop sage: R.lagrange_polynomial([(a^2+a,a),(a,1),(a^2,a^2+a+1)]) a^2*x^2 + a^2*x + a^2 }}} * Deprecate the method {{{__len__()}}} for a matrix group (Nicolas Thiery) -- The method {{{__len__()}}} of the class {{{MatrixGroup_gap}}} in {{{sage/groups/matrix_gps/matrix_group.py}}} is now deprecated and will be removed in a future release. To get the number of elements in a matrix group, users are advised to use the method {{{cardinality()}}} instead. The method {{{order()}}} is essentially the same as {{{cardinality()}}}, so {{{order()}}} will be deprecated in a future release. |
| Line 21: | Line 65: |
| * FIXME: summarize #6218 | * Optimize hyperelliptic curve arithmetic (Nick Alexander) -- Arithmetics with hyperelliptic curves can be up to 6x faster than previously. The following timing statistics were obtained using the maching sage.math: {{{ #BEFORE sage: F = GF(next_prime(10^30)) sage: x = F['x'].gen() sage: f = x^7 + x^2 + 1 sage: H = HyperellipticCurve(f, 2*x) sage: J = H.jacobian()(F) verbose 0 (902: multi_polynomial_ideal.py, dimension) Warning: falling back to very slow toy implementation. sage: Q = J(H.lift_x(F(1))) sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.65 s, sys: 0.02 s, total: 0.67 s Wall time: 0.68 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 1.08 s, sys: 0.00 s, total: 1.08 s Wall time: 1.08 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.72 s, sys: 0.02 s, total: 0.74 s Wall time: 0.74 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.67 s, sys: 0.00 s, total: 0.67 s Wall time: 0.67 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.66 s, sys: 0.00 s, total: 0.66 s Wall time: 0.66 s # AFTER sage: F = GF(next_prime(10^30)) sage: x = F['x'].gen() sage: f = x^7 + x^2 + 1 sage: H = HyperellipticCurve(f, 2*x) sage: J = H.jacobian()(F) verbose 0 (919: multi_polynomial_ideal.py, dimension) Warning: falling back to very slow toy implementation. sage: Q = J(H.lift_x(F(1))) sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.14 s, sys: 0.01 s, total: 0.15 s Wall time: 0.15 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.10 s, sys: 0.00 s, total: 0.10 s Wall time: 0.10 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.09 s, sys: 0.00 s, total: 0.09 s Wall time: 0.10 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.09 s, sys: 0.01 s, total: 0.10 s Wall time: 0.10 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.10 s, sys: 0.00 s, total: 0.10 s Wall time: 0.11 s }}} |
| Line 30: | Line 126: |
| * FIXME: summarize #6234 | * FIXME: summarize #6170 |
| Line 39: | Line 135: |
| * FIXME: summarize #6014 | * Hexads in {{{S(5,6,12)}}} and mathematical blackjack (David Joyner) -- Implements kittens, hexads and mathematical blackjack as described in the following papers: * R. Curtis. The Steiner system {{{S(5,6,12)}}}, the Mathieu group {{{M_{12}}}}, and the kitten. In M. Atkinson (ed.) Computational Group Theory, Academic Press, 1984. * J. Conway. Hexacode and tetracode -- MINIMOG and MOG. In M. Atkinson (ed.) Computational Group Theory, Academic Press, 1984. * J. Conway and N. Sloane. Lexicographic codes: error-correcting codes from game theory. IEEE Transactions on Information Theory, 32:337-348, 1986. * J. Kahane and A. Ryba. The hexad game. Electronic Journal of Combinatorics, 8, 2001. http://www.combinatorics.org/Volume_8/Abstracts/v8i2r11.html |
| Line 48: | Line 148: |
| * FIXME: summarize #6051 | * Enable Singular's coefficient rings which are not fields (Martin Albrecht) -- Singular 3-1-0 supports coefficient rings which are not fields. In particular, it supports {{{ZZ}}} and {{{ZZ/nZZ}}} now. These are now natively supported in Sage. |
| Line 54: | Line 154: |
| * FIXME: summarize #6185 | * S-box to CNF Conversion (Martin Albrecht) -- New method {{{cnf()}}} in the class {{{SBox}}} of {{{sage/crypto/mq/sbox.py}}} for converting an S-box to conjunctive normal form. Here are some examples on S-box to CNF conversion: {{{ sage: S = mq.SBox(1,2,0,3); S (1, 2, 0, 3) sage: S.cnf() [(1, 2, -3), (1, 2, 4), (1, -2, 3), (1, -2, -4), (-1, 2, -3), (-1, 2, -4), (-1, -2, 3), (-1, -2, 4)] sage: # convert this representation to the DIMACS format sage: print S.cnf(format='dimacs') p cnf 4 8 1 2 -3 0 1 2 4 0 1 -2 3 0 1 -2 -4 0 -1 2 -3 0 -1 2 -4 0 -1 -2 3 0 -1 -2 4 0 sage: # as a truth table sage: log = SymbolicLogic() sage: s = log.statement(S.cnf(format='symbolic')) sage: log.truthtable(s)[1:] [['False', 'False', 'False', 'False', 'False'], ['False', 'False', 'False', 'True', 'False'], ['False', 'False', 'True', 'False', 'False'], ['False', 'False', 'True', 'True', 'True'], ['False', 'True', 'False', 'False', 'True'], ['False', 'True', 'False', 'True', 'True'], ['False', 'True', 'True', 'False', 'True'], ['False', 'True', 'True', 'True', 'True'], ['True', 'False', 'False', 'False', 'True'], ['True', 'False', 'False', 'True', 'True'], ['True', 'False', 'True', 'False', 'True'], ['True', 'False', 'True', 'True', 'True'], ['True', 'True', 'False', 'False', 'True'], ['True', 'True', 'False', 'True', 'True'], ['True', 'True', 'True', 'False', 'True'], ['True', 'True', 'True', 'True', 'True']] }}} |
| Line 60: | Line 207: |
| * FIXME: summarize #5975 | * LaTeX output for (combinatorial) graphs (Robert Beezer, Fidel Barrera Cruz) -- Implement the option {{{tkz_style}}} to output graphs in LaTeX format so that they could be processed by pgf/tkz. Here's an example of the Petersen graph visualized using tkz: {{{ g = graphs.PetersenGraph() g.set_latex_options(tkz_style='Art') view(g, pdflatex=True) }}} {{attachment:petersen-latex.png}} |
| Line 148: | Line 301: |
| * FIXME: summarize #6298 |
Sage 4.0.2 Release Tour
Sage 4.0.2 was released on FIXME. For the official, comprehensive release note, please refer to FIXME. A nicely formatted version of this release tour can be found at FIXME. The following points are some of the foci of this release:
Algebra
Correct precision bound in hilbert_class_polynomial() and miscellaneous new functions (John Cremona) -- The two new functions are elliptic_j() in sage/functions/special.py, and is_primitive() in the class BinaryQF of sage/quadratic_forms/binary_qf.py. The function elliptic_j(z) returns the elliptic modular j-function evaluated at z. The function is_primitive() determines whether the binary quadratic form ax^2 + bxy + cy^2 satisfies gcd(a,b,c) = 1, i.e. that it is primitive. Here are some examples on using these new functions:
sage: elliptic_j(CC(i)) 1728.00000000000 sage: elliptic_j(sqrt(-2.0)) 8000.00000000000 sage: Q = BinaryQF([6,3,9]) sage: Q.is_primitive() False sage: Q = BinaryQF([1,1,1]) sage: Q.is_primitive() True
- Efficient Lagrange interpolation polynomial (Yann Laigle-Chapuy) -- Calculating the Lagrange interpolation polynomial of a set of points is now up to 48% faster than previously. The following timing statistics were obtained using the machine sage.math:
# BEFORE sage: R = PolynomialRing(QQ, 'x') sage: %timeit R.lagrange_polynomial([(0,1),(2,2),(3,-2),(-4,9)]) 1000 loops, best of 3: 824 µs per loop sage: R.lagrange_polynomial([(0,1),(2,2),(3,-2),(-4,9)]) -23/84*x^3 - 11/84*x^2 + 13/7*x + 1 sage: R = PolynomialRing(GF(2**3,'a'), 'x') sage: a = R.base_ring().gen() sage: timeit("R.lagrange_polynomial([(a^2+a,a),(a,1),(a^2,a^2+a+1)])") 625 loops, best of 3: 111 µs per loop sage: R.lagrange_polynomial([(a^2+a,a),(a,1),(a^2,a^2+a+1)]) a^2*x^2 + a^2*x + a^2 # AFTER sage: R = PolynomialRing(QQ, 'x') sage: %timeit R.lagrange_polynomial([(0,1),(2,2),(3,-2),(-4,9)]) 1000 loops, best of 3: 425 µs per loop sage: R.lagrange_polynomial([(0,1),(2,2),(3,-2),(-4,9)]) -23/84*x^3 - 11/84*x^2 + 13/7*x + 1 sage: R = PolynomialRing(GF(2**3,'a'), 'x') sage: a = R.base_ring().gen() sage: timeit("R.lagrange_polynomial([(a^2+a,a),(a,1),(a^2,a^2+a+1)])") 625 loops, best of 3: 86.4 µs per loop sage: R.lagrange_polynomial([(a^2+a,a),(a,1),(a^2,a^2+a+1)]) a^2*x^2 + a^2*x + a^2 Deprecate the method __len__() for a matrix group (Nicolas Thiery) -- The method __len__() of the class MatrixGroup_gap in sage/groups/matrix_gps/matrix_group.py is now deprecated and will be removed in a future release. To get the number of elements in a matrix group, users are advised to use the method cardinality() instead. The method order() is essentially the same as cardinality(), so order() will be deprecated in a future release.
Algebraic Geometry
- Optimize hyperelliptic curve arithmetic (Nick Alexander) -- Arithmetics with hyperelliptic curves can be up to 6x faster than previously. The following timing statistics were obtained using the maching sage.math:
#BEFORE sage: F = GF(next_prime(10^30)) sage: x = F['x'].gen() sage: f = x^7 + x^2 + 1 sage: H = HyperellipticCurve(f, 2*x) sage: J = H.jacobian()(F) verbose 0 (902: multi_polynomial_ideal.py, dimension) Warning: falling back to very slow toy implementation. sage: Q = J(H.lift_x(F(1))) sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.65 s, sys: 0.02 s, total: 0.67 s Wall time: 0.68 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 1.08 s, sys: 0.00 s, total: 1.08 s Wall time: 1.08 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.72 s, sys: 0.02 s, total: 0.74 s Wall time: 0.74 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.67 s, sys: 0.00 s, total: 0.67 s Wall time: 0.67 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.66 s, sys: 0.00 s, total: 0.66 s Wall time: 0.66 s # AFTER sage: F = GF(next_prime(10^30)) sage: x = F['x'].gen() sage: f = x^7 + x^2 + 1 sage: H = HyperellipticCurve(f, 2*x) sage: J = H.jacobian()(F) verbose 0 (919: multi_polynomial_ideal.py, dimension) Warning: falling back to very slow toy implementation. sage: Q = J(H.lift_x(F(1))) sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.14 s, sys: 0.01 s, total: 0.15 s Wall time: 0.15 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.10 s, sys: 0.00 s, total: 0.10 s Wall time: 0.10 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.09 s, sys: 0.00 s, total: 0.09 s Wall time: 0.10 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.09 s, sys: 0.01 s, total: 0.10 s Wall time: 0.10 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.10 s, sys: 0.00 s, total: 0.10 s Wall time: 0.11 s
Basic Arithmetic
Build
- FIXME: summarize #6170
Calculus
Coding Theory
Hexads in S(5,6,12) and mathematical blackjack (David Joyner) -- Implements kittens, hexads and mathematical blackjack as described in the following papers:
R. Curtis. The Steiner system S(5,6,12), the Mathieu group M_{12}, and the kitten. In M. Atkinson (ed.) Computational Group Theory, Academic Press, 1984.
- J. Conway. Hexacode and tetracode -- MINIMOG and MOG. In M. Atkinson (ed.) Computational Group Theory, Academic Press, 1984.
- J. Conway and N. Sloane. Lexicographic codes: error-correcting codes from game theory. IEEE Transactions on Information Theory, 32:337-348, 1986.
J. Kahane and A. Ryba. The hexad game. Electronic Journal of Combinatorics, 8, 2001. http://www.combinatorics.org/Volume_8/Abstracts/v8i2r11.html
Combinatorics
Commutative Algebra
Enable Singular's coefficient rings which are not fields (Martin Albrecht) -- Singular 3-1-0 supports coefficient rings which are not fields. In particular, it supports ZZ and ZZ/nZZ now. These are now natively supported in Sage.
Cryptography
S-box to CNF Conversion (Martin Albrecht) -- New method cnf() in the class SBox of sage/crypto/mq/sbox.py for converting an S-box to conjunctive normal form. Here are some examples on S-box to CNF conversion:
sage: S = mq.SBox(1,2,0,3); S (1, 2, 0, 3) sage: S.cnf() [(1, 2, -3), (1, 2, 4), (1, -2, 3), (1, -2, -4), (-1, 2, -3), (-1, 2, -4), (-1, -2, 3), (-1, -2, 4)] sage: # convert this representation to the DIMACS format sage: print S.cnf(format='dimacs') p cnf 4 8 1 2 -3 0 1 2 4 0 1 -2 3 0 1 -2 -4 0 -1 2 -3 0 -1 2 -4 0 -1 -2 3 0 -1 -2 4 0 sage: # as a truth table sage: log = SymbolicLogic() sage: s = log.statement(S.cnf(format='symbolic')) sage: log.truthtable(s)[1:] [['False', 'False', 'False', 'False', 'False'], ['False', 'False', 'False', 'True', 'False'], ['False', 'False', 'True', 'False', 'False'], ['False', 'False', 'True', 'True', 'True'], ['False', 'True', 'False', 'False', 'True'], ['False', 'True', 'False', 'True', 'True'], ['False', 'True', 'True', 'False', 'True'], ['False', 'True', 'True', 'True', 'True'], ['True', 'False', 'False', 'False', 'True'], ['True', 'False', 'False', 'True', 'True'], ['True', 'False', 'True', 'False', 'True'], ['True', 'False', 'True', 'True', 'True'], ['True', 'True', 'False', 'False', 'True'], ['True', 'True', 'False', 'True', 'True'], ['True', 'True', 'True', 'False', 'True'], ['True', 'True', 'True', 'True', 'True']]
Graph Theory
LaTeX output for (combinatorial) graphs (Robert Beezer, Fidel Barrera Cruz) -- Implement the option tkz_style to output graphs in LaTeX format so that they could be processed by pgf/tkz. Here's an example of the Petersen graph visualized using tkz:
g = graphs.PetersenGraph() g.set_latex_options(tkz_style='Art') view(g, pdflatex=True)
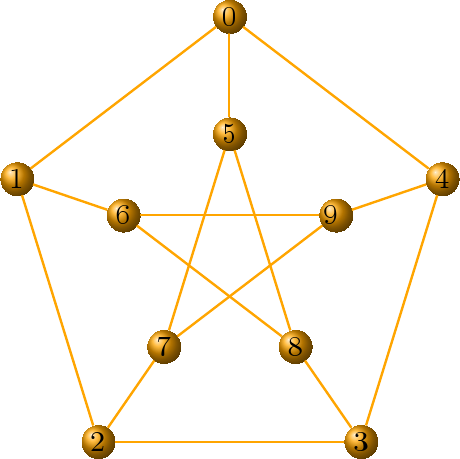
Graphics
Group Theory
- FIXME: summarize #6263
- FIXME: summarize #6123
Interfaces
Linear Algebra
- FIXME: summarize #6178
- FIXME: summarize #5510
- FIXME: summarize #2256
Miscellaneous
- FIXME: summarize #6089
- FIXME: summarize #6110
Modular Forms
Notebook
- FIXME: summarize #6259
- FIXME: summarize #6225
- FIXME: summarize #5371
Number Theory
- FIXME: summarize #5976
- FIXME: summarize #5842
- FIXME: summarize #6205
- FIXME: summarize #6193
- FIXME: summarize #6044
- FIXME: summarize #6046
Numerical
Packages
Upgrade NumPy to version 1.3.0 latest upstream release (Jason Grout).
Upgrade SciPy to version 0.7 latest upstream release (Jason Grout).
Upgrade Singular to version 3-1-0 latest upstream release (Martin Albrecht).
Upgrade FLINT to version 1.3.0 latest upstream release (Nick Alexander).
Update the MPIR spkg to version mpir-1.2.p3.spkg (Nick Alexander).
Remove Guava as a standard Sage package (David Joyner).
- FIXME: summarize #6298
Symbolics
