Differences between revisions 5 and 9 (spanning 4 versions)

Sage 4.0 Release Tour

Sage 4.0 was released on FIXME. For the official, comprehensive release note, please refer to sage-4.0.txt. A nicely formatted version of this release tour can be found at FIXME. The following points are some of the foci of this release:

Algebra

Deprecate the order() method on elements of rings (John Palmieri) -- The method order() of the class sage.structure.element.RingElement is now deprecated and will be removed in a future release. For additive or multiplicative order, use the additive_order or multiplicative_order method respectively.

Algebraic Geometry

Various invariants for genus 2 hyperelliptic curves (Nick Alexander) -- The following invariants for genus 2 hyperelliptic curves are implemented in the module sage/schemes/hyperelliptic_curves/hyperelliptic_g2_generic.py:
- the Clebsch invariants
- the Igusa-Clebsch invariants
- the absolute Igusa invariants

Basic Arithmetic

Build

Calculus

Coercion

Combinatorics

FIXME: summarize #5502
FIXME: summarize #5586

Commutative Algebra

FIXME: summarize #5576
FIXME: summarize #5609
FIXME: summarize #5566

Distribution

Doctest

Documentation

Geometry

Graph Theory

Graph colouring (Robert Miller) -- New method coloring() of the class sage.graphs.graph.Graph for obtaining the first (optimal) coloring found on a graph. Here are some examples on using this new method:
```
sage: G = Graph("Fooba")
sage: P = G.coloring()
sage: G.plot(partition=P)
sage: H = G.coloring(hex_colors=True)
sage: G.plot(vertex_colors=H)
```

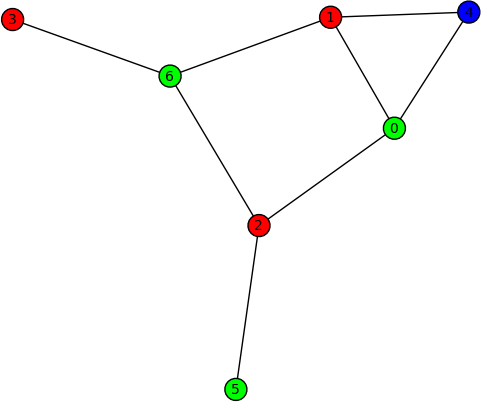
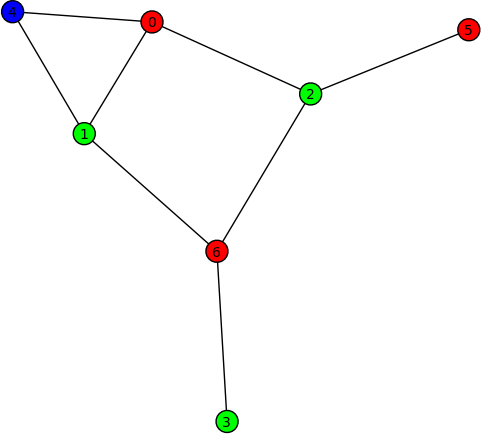
Graphics

FIXME: summarize #5249

Group Theory

FIXME: summarize #5664
FIXME: summarize #5844

Interfaces

Viewing Sage objects with a PDF viewer (Nicolas Thiery) -- Implements the option viewer="pdf" for the command view() so that one can invoke this command in the form view(object, viewer="pdf") in order to view object using a PDF viewer. Typical uses of this new optional argument include:
- You prefer to use a PDF viewer rather than a DVI viewer.
- You want to view LaTeX snippets which are not displayed well in DVI viewers (e.g. graphics produced using tikzpicture).
Change name of Pari's sum function when imported (Craig Citro) -- When Pari's sum function is imported, it is renamed to pari_sum in order to avoid conflict Python's sum function.

Linear Algebra

FIXME: summarize #5974
FIXME: summarize #5557
FIXME: summarize #5381

Miscellaneous

Allow use of pdflatex instead of latex (John Palmieri) -- One can now use pdflatex instead of latex in two different ways:
- Use a %pdflatex cell in a notebook; or
- Call latex.pdflatex(True)
after which any use of latex (in a %latex cell or using the view command) will use pdflatex. One visually appealing aspect of this is that if you have the most recent version of pgf installed, as well as the tkz-graph package, you can produce images like the following:

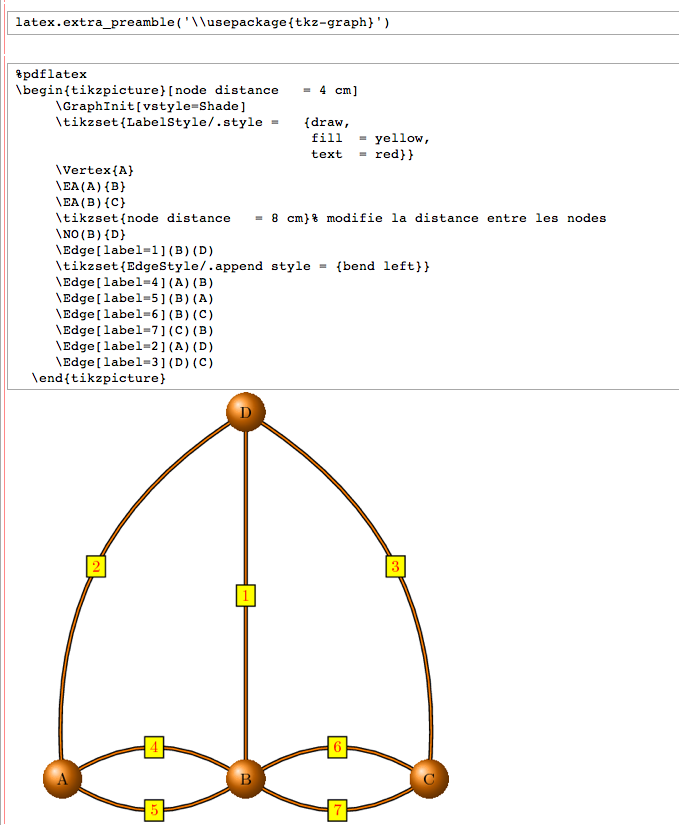
Modular Forms

FIXME: summarize #4337
FIXME: summarize #4357
FIXME: summarize #5262
FIXME: summarize #5792
FIXME: summarize #5796
FIXME: summarize #6019
FIXME: summarize #5924

Notebook

Number Theory

FIXME: summarize #5250
FIXME: summarize #6013
FIXME: summarize #6008
FIXME: summarize #6004

Numerical

Packages

FIXME: summarize #4223
FIXME: summarize #6031
FIXME: summarize #5934
FIXME: summarize #1338
FIXME: summarize #6032
FIXME: summarize #6024

P-adics

FIXME: summarize #5105

Quadratic Forms

Symbolics

Topology

Random simplicial complexes (John Palmieri) -- New method RandomComplex() in the module sage/homology/examples.py for producing a random d-dimensional simplicial complex on n vertices. Here's an example:
```
sage: simplicial_complexes.RandomComplex(6,12)
Simplicial complex with vertex set (0, 1, 2, 3, 4, 5, 6, 7) and facets {(0, 1, 2, 3, 4, 5, 6, 7)}
```

-  ⇤ ← Revision 5 as of 2009-05-15 08:12:27 → 
  Size: 2435
  Editor: Minh Nguyen
  Comment: Reminders to showcase features
+   ← Revision 9 as of 2009-05-18 08:09:19 → ⇥
  Size: 4690
  Editor: Minh Nguyen
  Comment: Summarize #6039, #6012, #5889
-Deletions are marked like this.
+Additions are marked like this.
 Line 10:
- * FIXME: summarize #5997
+ * Deprecate the {{{order()}}} method on elements of rings (John Palmieri) -- The method {{{order()}}} of the class {{{sage.structure.element.RingElement}}} is now deprecated and will be removed in a future release. For additive or multiplicative order, use the {{{additive_order}}} or {{{multiplicative_order}}} method respectively.
-Line 15:
+Line 16:
- * FIXME: summarize #6010
+ * Various invariants for genus 2 hyperelliptic curves (Nick Alexander) -- The following invariants for genus 2 hyperelliptic curves are implemented in the module {{{sage/schemes/hyperelliptic_curves/hyperelliptic_g2_generic.py}}}:
  * the Clebsch invariants
  * the Igusa-Clebsch invariants
  * the absolute Igusa invariants
-Line 60:
+Line 65:
- * FIXME: summarize #5913
+ * Graph colouring (Robert Miller) -- New method {{{coloring()}}} of the class {{{sage.graphs.graph.Graph}}} for obtaining the first (optimal) coloring found on a graph. Here are some examples on using this new method:
 {{{
sage: G = Graph("Fooba")
sage: P = G.coloring()
sage: G.plot(partition=P)
sage: H = G.coloring(hex_colors=True)
sage: G.plot(vertex_colors=H)
 }}}
{{attachment:graph-colour-1.png}}

{{attachment:graph-colour-2.png}}
-Line 78:
+Line 94:
- * Viewing Sage objects with a PDF viewer (INSERT CREDIT) -- Implements the option {{{viewer="pdf"}}} for the command {{{view()}}} so that one can invoke this command in the form {{{view(object, viewer="pdf")}}} in order to view {{{object}}} using a PDF viewer. Typical uses of this new optional argument include:
+ * Viewing Sage objects with a PDF viewer (Nicolas Thiery) -- Implements the option {{{viewer="pdf"}}} for the command {{{view()}}} so that one can invoke this command in the form {{{view(object, viewer="pdf")}}} in order to view {{{object}}} using a PDF viewer. Typical uses of this new optional argument include:
-Line 83:
+Line 99:
- * FIXME: summarize #6039
+ * Change name of Pari's {{{sum}}} function when imported (Craig Citro) -- When Pari's {{{sum}}} function is imported, it is renamed to {{{pari_sum}}} in order to avoid conflict Python's {{{sum}}} function.
-Line 97:
+Line 113:
- * FIXME: summarize #6012
+ * Allow use of {{{pdflatex}}} instead of {{{latex}}} (John Palmieri) -- One can now use {{{pdflatex}}} instead of {{{latex}}} in two different ways:
  * Use a {{{%pdflatex}}} cell in a notebook; or
  * Call {{{latex.pdflatex(True)}}} 
 after which any use of {{{latex}}} (in a {{{%latex}}} cell or using the {{{view}}} command) will use {{{pdflatex}}}. One visually appealing aspect of this is that if you have the most recent version of [[http://pgf.sourceforge.net|pgf]] installed, as well as the {{{tkz-graph}}} package, you can produce images like the following:
{{attachment:pgf-graph.png}}
-Line 142:
+Line 164:
+ * FIXME: summarize #1338

 * FIXME: summarize #6032

 * FIXME: summarize #6024
-Line 156:
+Line 184:
- * FIXME: summarize #5889
+ * Random simplicial complexes (John Palmieri) -- New method {{{RandomComplex()}}} in the module {{{sage/homology/examples.py}}} for producing a random {{{d}}}-dimensional simplicial complex on {{{n}}} vertices. Here's an example:
 {{{
sage: simplicial_complexes.RandomComplex(6,12)
Simplicial complex with vertex set (0, 1, 2, 3, 4, 5, 6, 7) and facets {(0, 1, 2, 3, 4, 5, 6, 7)}
 }}}

Diff for "ReleaseTours/sage-4.0"