Differences between revisions 2 and 85 (spanning 83 versions)
⇤ ← Revision 2 as of 2008-05-13 05:50:31 →
Size: 11127
Editor: was
Comment:
← Revision 85 as of 2017-03-18 14:43:37 → ⇥
Size: 63362
Editor: mforets
Comment: fix TypeError in Double Precision Root Finding Using Newton's Method
Deletions are marked like this. Additions are marked like this.
Line 2: Line 2:
goto [:interact:interact main page]

[[TableOfContents]]
 goto [[interact|interact main page]]

<<TableOfContents>>


== Root Finding Using Bisection ==
by William Stein

{{{#!sagecell
def bisect_method(f, a, b, eps):
    try:
        f = f._fast_float_(f.variables()[0])
    except AttributeError:
        pass
    intervals = [(a,b)]
    two = float(2); eps = float(eps)
    while True:
        c = (a+b)/two
        fa = f(a); fb = f(b); fc = f(c)
        if abs(fc) < eps: return c, intervals
        if fa*fc < 0:
            a, b = a, c
        elif fc*fb < 0:
            a, b = c, b
        else:
            raise ValueError, "f must have a sign change in the interval (%s,%s)"%(a,b)
        intervals.append((a,b))
pretty_print(html("<h1>Double Precision Root Finding Using Bisection</h1>"))
@interact
def _(f = cos(x) - x, a = float(0), b = float(1), eps=(-3,[-16..-1])):
     eps = 10^eps
     print "eps = %s"%float(eps)
     try:
         c, intervals = bisect_method(f, a, b, eps)
     except ValueError:
         print "f must have opposite sign at the endpoints of the interval"
         show(plot(f, a, b, color='red'), xmin=a, xmax=b)
     else:
         print "root =", c
         print "f(c) = %r"%f(x=c)
         print "iterations =", len(intervals)
         P = plot(f, a, b, color='red')
         h = (P.ymax() - P.ymin())/ (1.5*len(intervals))
         L = sum(line([(c,h*i), (d,h*i)]) for i, (c,d) in enumerate(intervals) )
         L += sum(line([(c,h*i-h/4), (c,h*i+h/4)]) for i, (c,d) in enumerate(intervals) )
         L += sum(line([(d,h*i-h/4), (d,h*i+h/4)]) for i, (c,d) in enumerate(intervals) )
         show(P + L, xmin=a, xmax=b)
}}}
{{attachment:bisect.png}}

== Newton's Method ==
Note that there is a more complicated Newton's method below.

by William Stein

https://cloud.sagemath.com/projects/19575ea0-317e-402b-be57-368d04c113db/files/pub/2801-2901/2824-Double%20Precision%20Root%20Finding%20Using%20Newton's%20Method.sagews

{{{#!sagecell
def newton_method(f, c, eps, maxiter=100):
    x = f.variables()[0]
    fprime = f.derivative(x)
    try:
        g = f._fast_float_(x)
        gprime = fprime._fast_float_(x)
    except AttributeError:
        g = f; gprime = fprime
    iterates = [c]
    for i in xrange(maxiter):
       fc = g(c)
       if abs(fc) < eps: return c, iterates
       c = c - fc/gprime(c)
       iterates.append(c)
    return c, iterates
    
var('x')
pretty_print(html("<h1>Double Precision Root Finding Using Newton's Method</h1>"))
@interact
def _(f = x^2 - 2, c = float(0.5), eps=(-3,[-16..-1]), interval=float(0.5)):
     eps = 10^(eps)
     print "eps = %s"%float(eps)
     z, iterates = newton_method(f, c, eps)
     print "root =", z
     print "f(c) = %r"%f(x=z)
     n = len(iterates)
     print "iterations =", n
     pretty_print(html(iterates))
     P = plot(f, (x,z-interval, z+interval), rgbcolor='blue')
     h = P.ymax(); j = P.ymin()
     L = sum(point((w,(n-1-float(i))/n*h), rgbcolor=(float(i)/n,0.2,0.3), pointsize=10) + \
             line([(w,h),(w,j)],rgbcolor='black',thickness=0.2) for i,w in enumerate(iterates))
     show(P + L, xmin=z-interval, xmax=z+interval)
}}}
{{attachment:newton.png}}
Line 9: Line 98:
{{{
@interact
def _(q1=(-1,(-3,3)), q2=(-2,(-3,3)), 
      cmap=['autumn', 'bone', 'cool', 'copper', 'gray', 'hot', 'hsv', 
https://cloud.sagemath.com/projects/19575ea0-317e-402b-be57-368d04c113db/files/pub/2801-2901/2823.sagews

{{{#!sagecell
@interact
def _(q1=(-1,(-3,3)), q2=(-2,(-3,3)),
      cmap=['autumn', 'bone', 'cool', 'copper', 'gray', 'hot', 'hsv',
Line 16: Line 108:
     C = contour_plot(f, (-2,2), (-2,2), plot_points=30, contours=15, cmap=cmap)      C = contour_plot(f, (x,-2,2), (y,-2,2), plot_points=30, contours=15, cmap=cmap)
Line 18: Line 110:
     show(plot3d(f, (x,-2,2), (y,-2,2)), figsize=5, viewer='tachyon')     
}}}
attachment:mountains.png		      show(plot3d(f, (x,-2,2), (y,-2,2)), figsize=5, viewer='tachyon')
}}}
{{attachment:mountains.png}}
Line 24: Line 116:
{{{
html('<h2>Tangent line grapher</h2>')
{{{#!sagecell
pretty_print(html('<h2>Tangent line grapher</h2>'))
Line 36: Line 129:
    fmax = f.find_maximum_on_interval(prange[0], prange[1])[0]
    fmin = f.find_minimum_on_interval(prange[0], prange[1])[0]		     fmax = f.find_local_maximum(prange[0], prange[1])[0]
    fmin = f.find_local_minimum(prange[0], prange[1])[0]
Line 40: Line 133:
attachment:tangents.png {{attachment:tangents.png}}

== Numerical integrals with the midpoint rule ==
by Marshall Hampton
{{{#!sagecell
#find_maximum_on_interval and find_minimum_on_interval are deprecated
#use find_local_maximum find_local_minimum instead
#see http://trac.sagemath.org/2607 for details -RRubalcaba

var('x')
@interact
def midpoint(n = slider(1,100,1,4), f = input_box(default = "x^2", type = str), start = input_box(default = "0", type = str), end = input_box(default = "1", type = str)):
    a = N(start)
    b = N(end)
    func = sage_eval(f, locals={'x':x})
    dx = (b-a)/n
    midxs = [q*dx+dx/2 + a for q in range(n)]
    midys = [func(x_val) for x_val in midxs]
    rects = Graphics()
    for q in range(n):
        xm = midxs[q]
        ym = midys[q]
        rects = rects + line([[xm-dx/2,0],[xm-dx/2,ym],[xm+dx/2,ym],[xm+dx/2,0]], rgbcolor = (1,0,0)) + point((xm,ym), rgbcolor = (1,0,0))
    min_y = min(0, sage.numerical.optimize.find_local_minimum(func,a,b)[0])
    max_y = max(0, sage.numerical.optimize.find_local_maximum(func,a,b)[0])
    pretty_print(html('<h3>Numerical integrals with the midpoint rule</h3>'))
    pretty_print(html('$\int_{a}^{b}{f(x) dx} {\\approx} \sum_i{f(x_i) \Delta x}$'))
    print "\n\nSage numerical answer: " + str(integral_numerical(func,a,b,max_points = 200)[0])
    print "Midpoint estimated answer: " + str(RDF(dx*sum([midys[q] for q in range(n)])))
    show(plot(func,a,b) + rects, xmin = a, xmax = b, ymin = min_y, ymax = max_y)
}}}
{{attachment:num_int.png}}

== Numerical integrals with various rules ==
by Nick Alexander (based on the work of Marshall Hampton)

{{{#!sagecell
# by Nick Alexander (based on the work of Marshall Hampton)
#find_maximum_on_interval and find_minimum_on_interval are deprecated
#use find_local_maximum find_local_minimum instead
#see http://trac.sagemath.org/2607 for details -RRubalcaba

var('x')
@interact
def midpoint(f = input_box(default = sin(x^2) + 2, type = SR),
    interval=range_slider(0, 10, 1, default=(0, 4), label="Interval"),
    number_of_subdivisions = slider(1, 20, 1, default=4, label="Number of boxes"),
    endpoint_rule = selector(['Midpoint', 'Left', 'Right', 'Upper', 'Lower'], nrows=1, label="Endpoint rule")):

    a, b = map(QQ, interval)
    t = sage.calculus.calculus.var('t')
    func = fast_callable(f(x=t), RDF, vars=[t])
    dx = ZZ(b-a)/ZZ(number_of_subdivisions)
   
    xs = []
    ys = []
    for q in range(number_of_subdivisions):
        if endpoint_rule == 'Left':
            xs.append(q*dx + a)
        elif endpoint_rule == 'Midpoint':
            xs.append(q*dx + a + dx/2)
        elif endpoint_rule == 'Right':
            xs.append(q*dx + a + dx)
        elif endpoint_rule == 'Upper':
            x = find_local_maximum(func, q*dx + a, q*dx + dx + a)[1]
            xs.append(x)
        elif endpoint_rule == 'Lower':
            x = find_local_minimum(func, q*dx + a, q*dx + dx + a)[1]
            xs.append(x)
    ys = [ func(x) for x in xs ]
         
    rects = Graphics()
    for q in range(number_of_subdivisions):
        xm = q*dx + dx/2 + a
        x = xs[q]
        y = ys[q]
        rects += line([[xm-dx/2,0],[xm-dx/2,y],[xm+dx/2,y],[xm+dx/2,0]], rgbcolor = (1,0,0))
        rects += point((x, y), rgbcolor = (1,0,0))
    min_y = min(0, find_local_minimum(func,a,b)[0])
    max_y = max(0, find_local_maximum(func,a,b)[0])

    # html('<h3>Numerical integrals with the midpoint rule</h3>')
    show(plot(func,a,b) + rects, xmin = a, xmax = b, ymin = min_y, ymax = max_y)
    
    def cap(x):
        # print only a few digits of precision
        if x < 1e-4:
            return 0
        return RealField(20)(x)
    sum_html = "%s \cdot \\left[ %s \\right]" % (dx, ' + '.join([ "f(%s)" % cap(i) for i in xs ]))
    num_html = "%s \cdot \\left[ %s \\right]" % (dx, ' + '.join([ str(cap(i)) for i in ys ]))
    
    numerical_answer = integral_numerical(func,a,b,max_points = 200)[0]
    estimated_answer = dx * sum([ ys[q] for q in range(number_of_subdivisions)])

    html(r'''
    <div class="math">
    \begin{align*}
      \int_{a}^{b} {f(x) \, dx} & = %s \\\
      \sum_{i=1}^{%s} {f(x_i) \, \Delta x}
      & = %s \\\
      & = %s \\\
      & = %s .
    \end{align*}
    </div>
    ''' % (numerical_answer, number_of_subdivisions, sum_html, num_html, estimated_answer))
}}}
{{attachment:num_int2.png}}

== Some polar parametric curves ==
by Marshall Hampton.
This is not very general, but could be modified to show other families of polar curves.
{{{#!sagecell
@interact
def para(n1 = slider(1,5,1,default = 2), n2 = slider(1,5,1,default = 3), a1 = slider(1,10,1/10,6/5), a2 = slider(1,10,1/10,6), b = slider(0,2,1/50,0)):
    var('t')
    pretty_print(html('$r=' + latex(b+sin(a1*t)^n1 + cos(a2*t)^n2)+'$'))
    p = parametric_plot((cos(t)*(b+sin(a1*t)^n1 + cos(a2*t)^n2), sin(t)*(b+sin(a1*t)^n1 + cos(a2*t)^n2)), (t,0, 20*pi), plot_points = 1024, rgbcolor = (0,0,0))
    show(p, figsize = [5,5], xmin = -2-b, xmax = 2+b, ymin = -2-b, ymax = 2+b, axes = False)
}}}
{{attachment:polarcurves1.png}}
Line 43: Line 256:
Enter symbolic functions $f$, $g$, and $a$, a range, then click the appropriate
button to compute and plot some combination of $f$, $g$, and $a$ along with $f$ and $g$.
This is inspired by the Matlab funtool GUI. 

{{{		 Enter symbolic functions $f$, $g$, and $a$, a range, then click the appropriate button to compute and plot some combination of $f$, $g$, and $a$ along with $f$ and $g$. This is inspired by the Matlab funtool GUI.

{{{#!sagecell
Line 49: Line 260:
Line 53: Line 263:
                       'f+a', 'f-a', 'f*a', 'f/a', 'f^a', 'f(x+a)', 'f(x*a)', 
                       'f+g', 'f-g', 'f*g', 'f/g', 'f(g)'], 		                        'f+a', 'f-a', 'f*a', 'f/a', 'f^a', 'f(x+a)', 'f(x*a)',
                       'f+g', 'f-g', 'f*g', 'f/g', 'f(g)'],
Line 57: Line 267:
Line 63: Line 272:
        return          return
Line 127: Line 336:
                  html('<center><font color="red">$f = %s$</font></center>'%latex(f))
    html('<center><font color="green">$g = %s$</font></center>'%latex(g))
    html('<center><font color="blue"><b>$h = %s = %s$</b></font></center>'%(lbl, latex(h)))		     pretty_print(html('<center><font color="red">$f = %s$</font></center>'%latex(f)))
    pretty_print(html('<center><font color="green">$g = %s$</font></center>'%latex(g)))
    pretty_print(html('<center><font color="blue"><b>$h = %s = %s$</b></font></center>'%(lbl, latex(h))))
Line 142: Line 349:

attachment:funtool.png		 {{attachment:funtool.png}}
Line 146: Line 352:
Line 149: Line 354:
This allows user to display the Newton-Raphson procedure one step at a time.
It uses the heuristic that, if any of the values of the controls change,
then the procedure should be re-started, else it should be continued.

{{{		 This allows user to display the Newton-Raphson procedure one step at a time. It uses the heuristic that, if any of the values of the controls change, then the procedure should be re-started, else it should be continued.

{{{#!sagecell
Line 157: Line 360:
State = Data = None # globals to allow incremental additions to graphics State = Data = None # globals to allow incremental changes in interaction data
Line 165: Line 368:
             step = ['Next','Reset'] ):              step = ['Next','Prev', 'Reset'] ):
Line 167: Line 370:
    prange = [xmin,xmax]
Line 170: Line 372:
        X = [RR(x0)] # restart the plot
        df = diff(f)
        Fplot = plot(f, prange[0], prange[1])
        Data = [X, df, Fplot]		         Data = [ 1 ] # reset the plot
Line 175: Line 374:

    X, df, Fplot = Data
    i = len(X) - 1 # compute and append the next x value
    xi = X[i]
    fi = RR(f(xi))
    fpi = RR(df(xi))
    xip1 = xi - fi/fpi
    X.append(xip1)

    msg = xip1s = None # now check x value for reasonableness		     elif step == 'Next':
        N, = Data
        Data = [ N+1 ]
    elif step == 'Prev':
        N, = Data
        if N > 1:
            Data = [ N-1 ]
    N, = Data
    df = diff(f)

    theplot = plot( f, xmin, xmax )
    theplot += text( '\n$x_0$', (x0,0), rgbcolor=(1,0,0),
                     vertical_alignment="bottom" if f(x0) < 0 else "top" )
    theplot += points( [(x0,0)], rgbcolor=(1,0,0) )

    Trace = []
    def Err( msg, Trace=Trace ):
        Trace.append( '<font color="red"><b>Error: %s!!</b></font>' % (msg,) )
    def Disp( s, color="blue", Trace=Trace ):
        Trace.append( """<font color="%s">$ %s $</font>""" % (color,s,) )

    Disp( """f(x) = %s""" % (latex(f),) )
    Disp( """f'(x) = %s""" % (latex(df),) )

    stop = False
Line 186: Line 400:
    if abs(xip1) > 10E6*(xmax-xmin):
        is_inf = True
        show_calcs = True
        msg = 'Derivative is 0!'
        xip1s = latex(xip1.sign()*infinity)
        X.pop()
    elif not ((xmin - 0.5*(xmax-xmin)) <= xip1 <= (xmax + 0.5*(xmax-xmin))):
        show_calcs = True
        msg = 'x value out of range; probable divergence!'
    if xip1s is None:
        xip1s = '%.4g' % (xip1,)

    def Disp( s, color="blue" ):
        if show_calcs:
            html( """<font color="%s">$ %s $</font>""" % (color,s,) )
    Disp( """f(x) = %s""" % (latex(f),) +
          """~~~~f'(x) = %s""" % (latex(df),) )
    Disp( """i = %d""" % (i,) +
          """~~~~x_{%d} = %.4g""" % (i,xi) +
          """~~~~f(x_{%d}) = %.4g""" % (i,fi) +
          """~~~~f'(x_{%d}) = %.4g""" % (i,fpi) )
    if msg:
        html( """<font color="red"><b>%s</b></font>""" % (msg,) )
        c = "red"
    else:
        c = "blue"
    Disp( r"""x_{%d} = %.4g - ({%.4g})/({%.4g}) = %s""" % (i+1,xi,fi,fpi,xip1s), color=c )

    Fplot += line( [(xi,0),(xi,fi)], linestyle=':', rgbcolor=(1,0,0) ) # vert dotted line
    Fplot += points( [(xi,0),(xi,fi)], rgbcolor=(1,0,0) )
    labi = text( '\nx%d\n' % (i,), (xi,0), rgbcolor=(1,0,0),
                 vertical_alignment="bottom" if fi < 0 else "top" )
    if is_inf:
        xl = xi - 0.05*(xmax-xmin)
        xr = xi + 0.05*(xmax-xmin)
        yl = yr = fi
    else:
        xl = min(xi,xip1) - 0.02*(xmax-xmin)
        xr = max(xi,xip1) + 0.02*(xmax-xmin)
        yl = -(xip1-xl)*fpi
        yr = (xr-xip1)*fpi
        Fplot += points( [(xip1,0)], rgbcolor=(0,0,1) ) # new x value
        labi += text( '\nx%d\n' % (i+1,), (xip1,0), rgbcolor=(1,0,0),
                 vertical_alignment="bottom" if fi < 0 else "top" )
    Fplot += line( [(xl,yl),(xr,yr)], rgbcolor=(1,0,0) ) # tangent

    show( Fplot+labi, xmin = prange[0], xmax = prange[1] )
    Data = [X, df, Fplot]
}}}


attachment:newtraph.png


== Coordinate Transformations ==		     xi = x0
    for i in range(N):
        fi = RR(f(xi))
        fpi = RR(df(xi))

        theplot += points( [(xi,fi)], rgbcolor=(1,0,0) )
        theplot += line( [(xi,0),(xi,fi)], linestyle=':', rgbcolor=(1,0,0) ) # vert dotted line
        Disp( """i = %d""" % (i,) )
        Disp( """~~~~x_{%d} = %.4g""" % (i,xi) )
        Disp( """~~~~f(x_{%d}) = %.4g""" % (i,fi) )
        Disp( """~~~~f'(x_{%d}) = %.4g""" % (i,fpi) )

        if fpi == 0.0:
            Err( 'Derivative is 0 at iteration %d' % (i+1,) )
            is_inf = True
            show_calcs = True
        else:
            xip1 = xi - fi/fpi
            Disp( r"""~~~~x_{%d} = %.4g - ({%.4g})/({%.4g}) = %.4g""" % (i+1,xi,fi,fpi,xip1) )
            if abs(xip1) > 10*(xmax-xmin):
                Err( 'Derivative is too close to 0!' )
                is_inf = True
                show_calcs = True
            elif not ((xmin - 0.5*(xmax-xmin)) <= xip1 <= (xmax + 0.5*(xmax-xmin))):
                Err( 'x value out of range; probable divergence!' )
                stop = True
                show_calcs = True
 
        if is_inf:
            xl = xi - 0.05*(xmax-xmin)
            xr = xi + 0.05*(xmax-xmin)
            yl = yr = fi
        else:
            xl = min(xi,xip1) - 0.01*(xmax-xmin)
            xr = max(xi,xip1) + 0.01*(xmax-xmin)
            yl = -(xip1-xl)*fpi
            yr = (xr-xip1)*fpi
            theplot += text( '\n$x_{%d}$' % (i+1,), (xip1,0), rgbcolor=(1,0,0),
                             vertical_alignment="bottom" if f(xip1) < 0 else "top" )
            theplot += points( [(xip1,0)], rgbcolor=(1,0,0) )

        theplot += line( [(xl,yl),(xr,yr)], rgbcolor=(1,0,0) ) # tangent

        if stop or is_inf:
            break
        epsa = 100.0*abs((xip1-xi)/xip1)
        nsf = 2 - log(2.0*epsa)/log(10.0)
        Disp( r"""~~~~~~~~\epsilon_a = \left|(%.4g - %.4g)/%.4g\right|\times100\%% = %.4g \%%""" % (xip1,xi,xip1,epsa) )
        Disp( r"""~~~~~~~~num.~sig.~fig. \approx %.2g""" % (nsf,) )
        xi = xip1

    show( theplot, xmin=xmin, xmax=xmax )
    if show_calcs:
        for t in Trace:
            html( t )
}}}
{{attachment:newtraph.png}}

== Coordinate Transformations (FIXME in Jupyter) ==
Line 243: Line 461:
{{{
{{{#!sagecell
Line 245: Line 464:
# polar coordinates
#(x,y)=(u*cos(v),u*sin(v)); (u_range,v_range)=([0..6],[0..2*pi,step=pi/12])

# weird example
(x,y)=(u^2-v^2,u*v+cos(u*v)); (u_range,v_range)=([-5..5],[-5..5])

thickness=4
square_length=.05
Line 246: Line 474:
@interact
def trans(x=input_box(u^2-v^2, label="x=",type=SR), \
    y=input_box(u*v, label="y=",type=SR), \
    t_val=slider(0,10,0.2,6, label="Length of curves"), \
    u_percent=slider(0,1,0.05,label="<font color='red'>u</font>", default=.7),
    v_percent=slider(0,1,0.05,label="<font color='blue'>v</font>", default=.7),
    u_range=input_box(range(-5,5,1), label="u lines"),
    v_range=input_box(range(-5,5,1), label="v lines")):
    thickness=4		 from functools import partial
@interact
def trans(x=input_box(x, label="x",type=SR),
         y=input_box(y, label="y",type=SR),
         u_percent=slider(0,1,0.05,label="<font color='red'>u</font>", default=.7),
         v_percent=slider(0,1,0.05,label="<font color='blue'>v</font>", default=.7),
         t_val=slider(0,10,0.2,6, label="Length"),
         u_range=input_box(u_range, label="u lines"),
         v_range=input_box(v_range, label="v lines")):

    x(u,v)=x
    y(u,v)=y
Line 259: Line 490:

    g1=sum([parametric_plot((SR(u.subs(u=i))._fast_float_('v'),v.subs(u=i)._fast_float_('v')), t_min,t_max, rgbcolor=(1,0,0)) for i in u_range])
    g2=sum([parametric_plot((u.subs(v=i)._fast_float_('u'),SR(v.subs(v=i))._fast_float_('u')), t_min,t_max, rgbcolor=(0,0,1)) for i in v_range])
    vline_straight=parametric_plot((SR(u.subs(v=v_val))._fast_float_('u'),SR(v.subs(v=v_val))._fast_float_('u')), t_min,t_max, rgbcolor=(0,0,1), linestyle='-',thickness=thickness)
    uline_straight=parametric_plot((SR(u.subs(u=u_val))._fast_float_('v'),SR(v.subs(u=u_val))._fast_float_('v')), t_min,t_max,rgbcolor=(1,0,0), linestyle='-',thickness=thickness)

    (g1+g2+vline_straight+uline_straight).save("uv_coord.png",aspect_ratio=1, figsize=[5,5], axes_labels=['$u$','$v$'])


    g3=sum([parametric_plot((x.subs(u=i)._fast_float_('v'),y.subs(u=i)._fast_float_('v')), t_min,t_max, rgbcolor=(1,0,0)) for i in u_range])
    g4=sum([parametric_plot((x.subs(v=i)._fast_float_('u'),y.subs(v=i)._fast_float_('u')), t_min,t_max, rgbcolor=(0,0,1)) for i in v_range])
    vline=parametric_plot((SR(x.subs(v=v_val))._fast_float_('u'),SR(y.subs(v=v_val))._fast_float_('u')), t_min,t_max, rgbcolor=(0,0,1), linestyle='-',thickness=thickness)
    uline=parametric_plot((SR(x.subs(u=u_val))._fast_float_('v'),SR(y.subs(u=u_val))._fast_float_('v')), t_min,t_max,rgbcolor=(1,0,0), linestyle='-',thickness=thickness)
    (g3+g4+vline+uline).save("xy_coord.png", aspect_ratio=1, figsize=[5,5], axes_labels=['$x$','$y$'])


    print jsmath("x=%s, \: y=%s"%(latex(x), latex(y)))
    print "<html><table><tr><td><img src='cell://uv_coord.png'/></td><td><img src='cell://xy_coord.png'/></td></tr></table></html>"
}}}

attachment:coordinate-transform-1.png
attachment:coordinate-transform-2.png		     uvplot=sum([parametric_plot((i,v), (v,t_min,t_max), color='red',axes_labels=['u','v'],figsize=[5,5]) for i in u_range])
    uvplot+=sum([parametric_plot((u,i), (u,t_min,t_max), color='blue',axes_labels=['u','v']) for i in v_range])
    uvplot+=parametric_plot((u,v_val), (u,t_min,t_max), rgbcolor=(0,0,1), linestyle='-',thickness=thickness)
    uvplot+=parametric_plot((u_val, v), (v,t_min,t_max),rgbcolor=(1,0,0), linestyle='-',thickness=thickness)
    pt=vector([u_val,v_val])
    du=vector([(t_max-t_min)*square_length,0])
    dv=vector([0,(t_max-t_min)*square_length])
    uvplot+=polygon([pt,pt+dv,pt+du+dv,pt+du],color='purple',alpha=0.7)
    uvplot+=line([pt,pt+dv,pt+du+dv,pt+du],color='green')

    T(u,v)=(x,y)
    xuv = fast_float(x,'u','v')
    yuv = fast_float(y,'u','v')
    xvu = fast_float(x,'v','u')
    yvu = fast_float(y,'v','u')
    xyplot=sum([parametric_plot((partial(xuv,i),partial(yuv,i)), (v,t_min,t_max), color='red', axes_labels=['x','y'],figsize=[5,5]) for i in u_range])
    xyplot+=sum([parametric_plot((partial(xvu,i),partial(yvu,i)), (u,t_min,t_max), color='blue') for i in v_range])
    xyplot+=parametric_plot((partial(xuv,u_val),partial(yuv,u_val)),(v,t_min,t_max),color='red', linestyle='-',thickness=thickness)
    xyplot+=parametric_plot((partial(xvu,v_val),partial(yvu,v_val)), (u,t_min,t_max), color='blue', linestyle='-',thickness=thickness)
    jacobian=abs(T.diff().det()).simplify_full()
    t_vals=[0..1,step=t_val*.01]
    vertices=[(x(*c),y(*c)) for c in [pt+t*dv for t in t_vals]]
    vertices+=[(x(*c),y(*c)) for c in [pt+dv+t*du for t in t_vals]]
    vertices+=[(x(*c),y(*c)) for c in [pt+(1-t)*dv+du for t in t_vals]]
    vertices+=[(x(*c),y(*c)) for c in [pt+(1-t)*du for t in t_vals]]
    xyplot+=polygon(vertices,color='purple',alpha=0.7)
    xyplot+=line(vertices,color='green')
    pretty_print(html("$T(u,v)=%s$"%(latex(T(u,v)))))
    pretty_print(html("Jacobian: $%s$"%latex(jacobian(u,v))))
    pretty_print(html("A very small region in $xy$ plane is approximately %0.4g times the size of the corresponding region in the $uv$ plane"%jacobian(u_val,v_val).n()))
    pretty_print(table([[uvplot,xyplot]]))
}}}


{{attachment:coordinate-transform-1.png}} {{attachment:coordinate-transform-2.png}}
Line 284: Line 528:
{{{
{{{#!sagecell
Line 294: Line 539:
    html('$f(x)\;=\;%s$'%latex(f))
    html('$\hat{f}(x;%s)\;=\;%s+\mathcal{O}(x^{%s})$'%(x0,latex(ft),order+1))		     pretty_print(html('$f(x)\;=\;%s$'%latex(f)))
    pretty_print(html('$\hat{f}(x;%s)\;=\;%s+\mathcal{O}(x^{%s})$'%(x0,latex(ft),order+1)))
Line 298: Line 543:
attachment:taylor_series_animated.gif {{attachment:taylor_series_animated.gif}}

== Illustration of the precise definition of a limit ==
by John Perry

I'll break tradition and put the image first. Apologies if this is Not A Good Thing.

{{attachment:snapshot_epsilon_delta.png}}

{{{#!sagecell
pretty_print(html("<h2>Limits: <i>ε-δ</i></h2>"))
pretty_print(html("This allows you to estimate which values of <i>δ</i> guarantee that <i>f</i> is within <i>ε</i> units of a limit."))
pretty_print(html("<ul><li>Modify the value of <i>f</i> to choose a function.</li>"))
pretty_print(html("<li>Modify the value of <i>a</i> to change the <i>x</i>-value where the limit is being estimated.</li>"))
pretty_print(html("<li>Modify the value of <i>L</i> to change your guess of the limit.</li>"))
pretty_print(html("<li>Modify the values of <i>δ</i> and <i>ε</i> to modify the rectangle.</li></ul>"))
pretty_print(html("If the blue curve passes through the pink boxes, your values for <i>δ</i> and/or <i>ε</i> are probably wrong."))
@interact
def delta_epsilon(f = input_box(default=(x^2-x)/(x-1)), a=input_box(default=1), L = input_box(default=1), delta=input_box(label="δ",default=0.1), epsilon=input_box(label="ε",default=0.1), xm=input_box(label="<i>x</i><sub>min</sub>",default=-1), xM=input_box(label="<i>x</i><sub>max</sub>",default=4)):
    f_left_plot = plot(f,xm,a-delta/3,thickness=2)
    f_right_plot = plot(f,a+delta/3,xM,thickness=2)
    epsilon_line_1 = line([(xm,L-epsilon),(xM,L-epsilon)], rgbcolor=(0.5,0.5,0.5),linestyle='--')
    epsilon_line_2 = line([(xm,L+epsilon),(xM,L+epsilon)], rgbcolor=(0.5,0.5,0.5),linestyle='--')
    ym = min(f_right_plot.ymin(),f_left_plot.ymin())
    yM = max(f_right_plot.ymax(),f_left_plot.ymax())
    bad_region_1 = polygon([(a-delta,L+epsilon),(a-delta,yM),(a+delta,yM),(a+delta,L+epsilon)], rgbcolor=(1,0.6,0.6))
    bad_region_2 = polygon([(a-delta,L-epsilon),(a-delta,ym),(a+delta,ym),(a+delta,L-epsilon)], rgbcolor=(1,0.6,0.6))
    aL_point = point((a,L),rgbcolor=(1,0,0),pointsize=20)
    delta_line_1 = line([(a-delta,ym),(a-delta,yM)],rgbcolor=(0.5,0.5,0.5),linestyle='--')
    delta_line_2 = line([(a+delta,ym),(a+delta,yM)],rgbcolor=(0.5,0.5,0.5),linestyle='--')
    (f_left_plot +f_right_plot +epsilon_line_1 +epsilon_line_2 +delta_line_1 +delta_line_2 +aL_point +bad_region_1 +bad_region_2).show(xmin=xm,xmax=xM)
}}}

== A graphical illustration of sin(x)/x -> 1 as x-> 0 ==
by Wai Yan Pong

{{{#!sagecell
x=var('x')
@interact
def _(x = slider(-7/10,7/10,1/20,1/2)):
    pretty_print(html('<h3>A graphical illustration of $\lim_{x -> 0} \sin(x)/x =1$</h3>'))
    pretty_print(html('Below is the unit circle, so the length of the <font color=red>red line</font> is |sin(x)|'))
    pretty_print(html('and the length of the <font color=blue>blue line</font> is |tan(x)| where x is the length of the arc.'))
    pretty_print(html('From the picture, we see that |sin(x)| $\le$ |x| $\le$ |tan(x)|.'))
    pretty_print(html('It follows easily from this that cos(x) $\le$ sin(x)/x $\le$ 1 when x is near 0.'))
    pretty_print(html('As $\lim_{x ->0} \cos(x) =1$, we conclude that $\lim_{x -> 0} \sin(x)/x =1$.'))
    if not (x == 0):
        pretty_print("sin(x)/x = "+str(sin(float(x))/float(x)))
    elif x == 0:
        pretty_print("The limit of sin(x)/x as x tends to 0 is 1.")
    C=circle((0,0),1, rgbcolor='black')
    mvp = (cos(x),sin(x));tpt = (1, tan(x))
    p1 = point(mvp, pointsize=30, rgbcolor='red'); p2 = point((1,0), pointsize=30, rgbcolor='red')
    line1 = line([(0,0),tpt], rgbcolor='black'); line2 = line([(cos(x),0),mvp], rgbcolor='red')
    line3 = line([(0,0),(1,0)], rgbcolor='black'); line4 = line([(1,0),tpt], rgbcolor='blue')
    result = C+p1+p2+line1+line2+line3+line4
    result.show(aspect_ratio=1, figsize=[3,3], axes=False)
}}}
{{attachment:sinelimit.png}}

== Quadric Surface Plotter ==
by Marshall Hampton. This is pretty simple, so I encourage people to spruce it up. In particular, it isn't set up to show all possible types of quadrics.
{{{#!sagecell
var('x,y,z')
quadrics = {'Ellipsoid':x^2+y^2+z^2-1,'Elliptic paraboloid':x^2+y^2-z,'Hyperbolic paraboloid':x^2-y^2-z, '1-Sheeted Hyperboloid':x^2+y^2-z^2-1,'2-Sheeted Hyperboloid':x^2-y^2-z^2-1, 'Cone':x^2+y^2-z^2}
@interact
def quads(q = selector(quadrics.keys()), a = slider(0,5,1/2,default = 1)):
    f = quadrics[q].subs({x:x*a^(1/2)})
    if a==0 or q=='Cone': html('<center>$'+latex(f)+' \ $'+ '(degenerate)</center>')
    else: html('<center>$'+latex(f)+'$ </center>')
    p = implicit_plot3d(f,(x,-2,2),(y,-2,2),(z,-2,2), plot_points = 75)
    show(p)
}}}
{{attachment:quadrics.png}}

== The midpoint rule for numerically integrating a function of two variables ==
by Marshall Hampton
{{{#!sagecell
from sage.plot.plot3d.platonic import index_face_set
def cuboid(v1,v2,**kwds):
    """
    Cuboid defined by corner points v1 and v2.
    """
    ptlist = []
    for vi in (v1,v2):
        for vj in (v1,v2):
            for vk in (v1,v2):
                ptlist.append([vi[0],vj[1],vk[2]])
    f_incs = [[0, 2, 6, 4], [0, 1, 3, 2], [0, 1, 5, 4], [1, 3, 7, 5], [2, 3, 7, 6], [4, 5, 7, 6]]
    
    if 'aspect_ratio' not in kwds:
        kwds['aspect_ratio'] = [1,1,1]
    return index_face_set(f_incs,ptlist,enclosed = True, **kwds)
var('x,y')
R16 = RealField(16)
npi = RDF(pi)

pretty_print(html("<h1>The midpoint rule for a function of two variables</h1>"))
@interact
def midpoint2d(func = input_box('y*sin(x)/x+sin(y)',type=str,label='function of x and y'), nx = slider(2,20,1,3,label='x subdivisions'), ny = slider(2,20,1,3,label='y subdivisions'), x_start = slider(-10,10,.1,0), x_end = slider(-10,10,.1,3*npi), y_start= slider(-10,10,.1,0), y_end= slider(-10,10,.1,3*npi)):
    f = sage_eval('lambda x,y: ' + func)
    delx = (x_end - x_start)/nx
    dely = (y_end - y_start)/ny
    xvals = [RDF(x_start + (i+1.0/2)*delx) for i in range(nx)]
    yvals = [RDF(y_start + (i+1.0/2)*dely) for i in range(ny)]
    num_approx = 0
    cubs = []
    darea = delx*dely
    for xv in xvals:
        for yv in yvals:
            num_approx += f(xv,yv)*darea
            cubs.append(cuboid([xv-delx/2,yv-dely/2,0],[xv+delx/2,yv+dely/2,f(xv,yv)], opacity = .5, rgbcolor = (1,0,0)))
    pretty_print(html("$$\int_{"+str(R16(y_start))+"}^{"+str(R16(y_end))+"} "+ "\int_{"+str(R16(x_start))+"}^{"+str(R16(x_end))+"} "+func+"\ dx \ dy$$"))
    pretty_print(html('<p style="text-align: center;">Numerical approximation: ' + str(num_approx)+'</p>'))
    p1 = plot3d(f,(x,x_start,x_end),(y,y_start,y_end))
    show(p1+sum(cubs))
}}}
{{attachment:numint2d.png}}

== Gaussian (Legendre) quadrature ==
by Jason Grout

The output shows the points evaluated using Gaussian quadrature (using a weight of 1, so using Legendre polynomials). The vertical bars are shaded to represent the relative weights of the points (darker = more weight). The error in the trapezoid, Simpson, and quadrature methods is both printed out and compared through a bar graph. The "Real" error is the error returned from scipy on the definite integral.
{{{#!sagecell
import scipy
import numpy
from scipy.special.orthogonal import p_roots, t_roots, u_roots
from scipy.integrate import quad, trapz, simps
from sage.ext.fast_eval import fast_float
from numpy import linspace
show_weight_graph=False
# 'Hermite': {'w': e**(-x**2), 'xmin': -numpy.inf, 'xmax': numpy.inf, 'func': h_roots},
# 'Laguerre': {'w': e**(-x), 'xmin': 0, 'xmax': numpy.inf, 'func': l_roots},

methods = {'Legendre': {'w': 1, 'xmin': -1, 'xmax': 1, 'func': p_roots},
     'Chebyshev': {'w': 1/sqrt(1-x**2), 'xmin': -1, 'xmax': 1, 'func': t_roots},
     'Chebyshev2': {'w': sqrt(1-x**2), 'xmin': -1, 'xmax': 1, 'func': u_roots},
     'Trapezoid': {'w': 1, 'xmin': -1, 'xmax': 1,
        'func': lambda n: (linspace(-1r,1,n), numpy.array([1.0r]+[2.0r]*(n-2)+[1.0r])*1.0r/n)},
     'Simpson': {'w': 1, 'xmin': -1, 'xmax': 1,
        'func': lambda n: (linspace(-1r,1,n),
            numpy.array([1.0r]+[4.0r,2.0r]*int((n-3.0r)/2.0r)+[4.0r,1.0r])*2.0r/(3.0r*n))}}
var("x")
def box(center, height, area,**kwds):
    width2 = 1.0*area/height/2.0
    return polygon([(center-width2,0),
        (center+width2,0),(center+width2,height),(center-width2,height)],**kwds)
    
    
@interact
def weights(n=slider(1,30,1,default=10),f=input_box(default=3*x+cos(10*x),type=SR),
    show_method=["Legendre", "Chebyshev", "Chebyshev2", "Trapezoid","Simpson"]):
    ff = fast_float(f,'x')
    method = methods[show_method]
    xcoords,w = (method['func'])(int(n))
    xmin = method['xmin']
    xmax = method['xmax']
    plot_min = max(xmin, -10)
    plot_max = min(xmax, 10)
    scaled_func = f*method['w']
    scaled_ff = fast_float(scaled_func, 'x')

    coords = zip(xcoords,w)
    max_weight = max(w)
    coords_scaled = zip(xcoords,w/max_weight)

    f_graph = plot(scaled_func,plot_min,plot_max)
    boxes = sum(box(x,ff(x),w*ff(x),rgbcolor=(0.5,0.5,0.5),alpha=0.3) for x,w in coords)
    stems = sum(line([(x,0),(x,scaled_ff(x))],rgbcolor=(1-y,1-y,1-y),
        thickness=2,markersize=6,alpha=y) for x,y in coords_scaled)
    points = sum([point([(x,0),
        (x,scaled_ff(x))],rgbcolor='black',pointsize=30) for x,_ in coords])
    graph = stems+points+f_graph+boxes
    if show_weight_graph:
        graph += line([(x,y) for x,y in coords_scaled], rgbcolor='green',alpha=0.4)
    
    show(graph,xmin=plot_min,xmax=plot_max,aspect_ratio="auto")

    approximation = sum([w*ff(x) for x,w in coords])
    integral,integral_error = scipy.integrate.quad(scaled_ff, xmin, xmax)
    x_val = linspace(min(xcoords), max(xcoords),n)
    y_val = map(scaled_ff,x_val)
    trapezoid = integral-trapz(y_val, x_val)
    simpson = integral-simps(y_val, x_val)
    pretty_print(html("$$\sum_{i=1}^{i=%s}w_i\left(%s\\right)= %s\\approx %s =\int_{-1}^{1}%s \,dx$$"%(n,
        latex(f), approximation, integral, latex(scaled_func))))
    error_data = [trapezoid, simpson, integral-approximation,integral_error]
    print "Trapezoid: %s, Simpson: %s, \nMethod: %s, Real: %s"%tuple(error_data)
    show(bar_chart(error_data,width=1),ymin=min(error_data), ymax=max(error_data))
}}}
{{attachment:quadrature1.png}}
{{attachment:quadrature2.png}}

== Vector Calculus, 2-D Motion ==
By Rob Beezer

A fast_float() version is available in a [[http://buzzard.ups.edu/sage/motion-2d.sws|worksheet]]

{{{#!sagecell
# 2-D motion and vector calculus
# Copyright 2009, Robert A. Beezer
# Creative Commons BY-SA 3.0 US
#
# 2009/02/15 Built on Sage 3.3.rc0
# 2009/02/17 Improvements from Jason Grout
#
# variable parameter is t
# later at a particular value named t0
#
var('t')
#
# parameter range
#
start=0
stop=2*pi
#
# position vector definition
# edit here for new example
# example is wide ellipse
# adjust x, extents in final show()
#
position=vector( (4*cos(t), sin(t)) )
#
# graphic of the motion itself
#
path = parametric_plot( position(t).list(), (t, start, stop), color = "black" )
#
# derivatives of motion, lengths, unit vectors, etc
#
velocity = derivative(position(t), t)
acceleration = derivative(velocity(t), t)
speed = velocity.norm()
speed_deriv = derivative(speed, t)
tangent = (1/speed)*velocity
dT = derivative(tangent(t), t)
normal = (1/dT.norm())*dT
#
# interact section
# slider for parameter, 24 settings
# checkboxes for various vector displays
# computations at one value of parameter, t0
#
@interact
def _(t0 = slider(float(start), float(stop), float((stop-start)/24), float(start) , label = "Parameter"),
      pos_check = ("Position", True),
      vel_check = ("Velocity", False),
      tan_check = ("Unit Tangent", False),
      nor_check = ("Unit Normal", False),
      acc_check = ("Acceleration", False),
      tancomp_check = ("Tangential Component", False),
      norcomp_check = ("Normal Component", False)
       ):
    #
    # location of interest
    #
    pos_tzero = position(t0)
    #
    # various scalar quantities at point
    #
    speed_component = speed(t0)
    tangent_component = speed_deriv(t0)
    normal_component = sqrt( acceleration(t0).norm()^2 - tangent_component^2 )
    curvature = normal_component/speed_component^2
    #
    # various vectors, mostly as arrows from the point
    #
    pos = arrow((0,0), pos_tzero, rgbcolor=(0,0,0))
    tan = arrow(pos_tzero, pos_tzero + tangent(t0), rgbcolor=(0,1,0) )
    vel = arrow(pos_tzero, pos_tzero + velocity(t0), rgbcolor=(0,0.5,0))
    nor = arrow(pos_tzero, pos_tzero + normal(t0), rgbcolor=(0.5,0,0))
    acc = arrow(pos_tzero, pos_tzero + acceleration(t0), rgbcolor=(1,0,1))
    tancomp = arrow(pos_tzero, pos_tzero + tangent_component*tangent(t0), rgbcolor=(1,0,1) )
    norcomp = arrow(pos_tzero, pos_tzero + normal_component*normal(t0), rgbcolor=(1,0,1))
    #
    # accumulate the graphic based on checkboxes
    #
    picture = path
    if pos_check:
        picture = picture + pos
    if vel_check:
        picture = picture + vel
    if tan_check:
        picture = picture+ tan
    if nor_check:
        picture = picture + nor
    if acc_check:
        picture = picture + acc
    if tancomp_check:
        picture = picture + tancomp
    if norcomp_check:
        picture = picture + norcomp
    #
    # print textual info
    #
    print "Position vector defined as r(t)=", position(t)
    print "Speed is ", N(speed(t0))
    print "Curvature is ", N(curvature)
    #
    # show accumulated graphical info
    # adjust x-,y- extents to get best plot
    #
    show(picture, xmin=-4,xmax=4, ymin=-1.5,ymax=1.5,aspect_ratio=1)
}}}
{{attachment:motion2d.png}}

== Vector Calculus, 3-D Motion (FIXME) ==
by Rob Beezer

Available as a [[http://buzzard.ups.edu/sage/motion-d.sws|worksheet]]

{{{#!sagecell
# 3-D motion and vector calculus
# Copyright 2009, Robert A. Beezer
# Creative Commons BY-SA 3.0 US
#
#
# 2009/02/15 Built on Sage 3.3.rc0
# 2009/02/17 Improvements from Jason Grout
#
# variable parameter is t
# later at a particular value named t0
#
# un-comment double hash (##) to get
# time-consuming torsion computation
#
var('t')
#
# parameter range
#
start=-4*pi
stop=8*pi
#
# position vector definition
# edit here for new example
# example is wide ellipse
# adjust figsize in final show() to get accurate aspect ratio
#
a=1/(8*pi)
c=(3/2)*a
position=vector( (exp(a*t)*cos(t), exp(a*t)*sin(t), exp(c*t)) )
#
# graphic of the motion itself
#
path = parametric_plot3d( position(t).list(), (t, start, stop), color = "black" )
#
# derivatives of motion, lengths, unit vectors, etc
#
velocity = derivative( position(t), t)
acceleration = derivative(velocity(t), t)
speed = velocity.norm()
speed_deriv = derivative(speed, t)
tangent = (1/speed)*velocity
dT = derivative(tangent(t), t)
normal = (1/dT.norm())*dT
binormal = tangent.cross_product(normal)
## dB = derivative(binormal(t), t)
#
# interact section
# slider for parameter, 24 settings
# checkboxes for various vector displays
# computations at one value of parameter, t0
#
@interact
def _(t0 = slider(float(start), float(stop), float((stop-start)/24), float(start) , label = "Parameter"),
      pos_check = ("Position", True),
      vel_check = ("Velocity", False),
      tan_check = ("Unit Tangent", False),
      nor_check = ("Unit Normal", False),
      bin_check = ("Unit Binormal", False),
      acc_check = ("Acceleration", False),
      tancomp_check = ("Tangential Component", False),
      norcomp_check = ("Normal Component", False)
       ):
    #
    # location of interest
    #
    pos_tzero = position(t0)
    #
    # various scalar quantities at point
    #
    speed_component = speed(t0)
    tangent_component = speed_deriv(t0)
    normal_component = sqrt( acceleration(t0).norm()^2 - tangent_component^2 )
    curvature = normal_component/speed_component^2
    ## torsion = (1/speed_component)*(dB(t0)).dot_product(normal(t0))
    #
    # various vectors, mostly as arrows from the point
    #
    pos = arrow3d((0,0,0), pos_tzero, rgbcolor=(0,0,0))
    tan = arrow3d(pos_tzero, pos_tzero + tangent(t0), rgbcolor=(0,1,0) )
    vel = arrow3d(pos_tzero, pos_tzero + velocity(t0), rgbcolor=(0,0.5,0))
    nor = arrow3d(pos_tzero, pos_tzero + normal(t0), rgbcolor=(0.5,0,0))
    bin = arrow3d(pos_tzero, pos_tzero + binormal(t0), rgbcolor=(0,0,0.5))
    acc = arrow3d(pos_tzero, pos_tzero + acceleration(t0), rgbcolor=(1,0,1))
    tancomp = arrow3d(pos_tzero, pos_tzero + tangent_component*tangent(t0), rgbcolor=(1,0,1) )
    norcomp = arrow3d(pos_tzero, pos_tzero + normal_component*normal(t0), rgbcolor=(1,0,1))
    #
    # accumulate the graphic based on checkboxes
    #
    picture = path
    if pos_check:
        picture = picture + pos
    if vel_check:
        picture = picture + vel
    if tan_check:
        picture = picture+ tan
    if nor_check:
        picture = picture + nor
    if bin_check:
        picture = picture + bin
    if acc_check:
        picture = picture + acc
    if tancomp_check:
        picture = picture + tancomp
    if norcomp_check:
        picture = picture + norcomp
    #
    # print textual info
    #
    print "Position vector: r(t)=", position(t)
    print "Speed is ", N(speed(t0))
    print "Curvature is ", N(curvature)
    ## print "Torsion is ", N(torsion)
    print
    print "Right-click on graphic to zoom to 400%"
    print "Drag graphic to rotate"
    #
    # show accumulated graphical info
    #
    show(picture, aspect_ratio=[1,1,1])
}}}
{{attachment:motion3d.png}}

== Multivariate Limits by Definition ==
by John Travis

http://sagenb.mc.edu/home/pub/97/

{{{#!sagecell
## An interactive way to demonstrate limits of multivariate functions of the form z = f(x,y)
##
## John Travis
## Mississippi College
##
## Spring 2011
##

# Starting point for radius values before collapsing in as R approaches 0.
# Functions ought to be "reasonable" within a circular domain of radius R surrounding
# the desired (x_0,y_0).
var('x,y,z')
Rmin=1/10
Rmax=2
@interact(layout=dict(top=[['f'],['x0'],['y0']],
bottom=[['in_3d','curves','R','graphjmol']]))
def _(f=input_box((x^2-y^2)/(x^2+y^2),width=30,label='$f(x)$'),
        R=slider(Rmin,Rmax,1/10,Rmax,label=',   $R$'),
        x0=input_box(0,width=10,label='$x_0$'),
        y0=input_box(0,width=10,label='$y_0$'),
        curves=checkbox(default=false,label='Show curves'),
        in_3d=checkbox(default=false,label='3D'),
        graphjmol=checkbox(default=true,label='Interactive graph')):
    if graphjmol:
        view_method = 'jmol'
    else:
        view_method = 'tachyon'

# converting f to cylindrical coordinates.
    g(r,t) = f(x=r*cos(t)+x0,y=r*sin(t)+y0)

# Sage graphing transformation used to see the original surface.
    cylinder = (r*cos(t)+x0,r*sin(t)+y0,z)
    surface = plot3d(g,(t,0,2*pi),(r,1/100,Rmax),transformation=cylinder,opacity=0.2)
    
# Regraph the surface for smaller and smaller radii controlled by the slider.
    collapsing_surface = plot3d(g,(t,0,2*pi),(r,1/100,R),transformation=cylinder,rgbcolor=(0,1,0))
    
    G = surface+collapsing_surface
    pretty_print(html('Enter $(x_0 ,y_0 )$ above and see what happens as $ R \\rightarrow 0 $.'))
    pretty_print(html('The surface has a limit as $(x,y) \\rightarrow $ ('+str(x0)+','+str(y0)+') if the green region collapses to a point.'))

# If checked, add a couple of curves on the surface corresponding to limit as x->x0 for y=x^(3/5),
# and as y->y0 for x=y^(3/5). Should make this more robust but perhaps using
# these relatively obtuse curves could eliminate problems.

    if curves:
        curve_x = parametric_plot3d([x0-t,y0-t^(3/5),f(x=x0-t,y=y0-t^(3/5))],(t,Rmin,Rmax),color='red',thickness=10)
        curve_y = parametric_plot3d([x0+t^(3/5),y0+t,f(x=x0+t^(3/5),y=y0+t)],(t,Rmin,Rmax),color='red',thickness=10)
        R2 = Rmin/4
        G += arrow((x0-Rmin,y0-Rmin^(3/5),f(x=x0-Rmin,y=y0-Rmin^(3/5))),(x0-R2,y0-R2^(3/5),f(x=x0-R2,y=y0-R2^(3/5))),size=30 )
        G += arrow((x0+Rmin^(3/5),y0+Rmin,f(x=x0+Rmin^(3/5),y=y0+Rmin)),(x0+R2^(3/5),y0+R2,f(x=x0+R2^(3/5),y=y0+R2)),size=30 )

        limit_x = limit(f(x=x0-t,y=y0-t^(3/5)),t=0)
        limit_y = limit(f(x=x0+t^(3/5),y=y0+t),t=0)
        text_x = text3d(limit_x,(x0,y0,limit_x))
        text_y = text3d(limit_y,(x0,y0,limit_y))
        G += curve_x+curve_y+text_x+text_y
 
    
        pretty_print(html('The red curves represent a couple of trajectories on the surface. If they do not meet, then'))
        pretty_print(html('there is also no limit. (If computer hangs up, likely the computer can not do these limits.)'))
        pretty_print(html('\n<center><font color="red">$\lim_{(x,?)\\rightarrow(x_0,y_0)} f(x,y) =%s$</font>'%str(limit_x)+' and <font color="red">$\lim_{(?,y)\\rightarrow(x_0,y_0)} f(x,y) =%s$</font></center>'%str(limit_y)))
        
    if in_3d:
        show(G,stereo="redcyan",viewer=view_method)
    else:
        show(G,perspective_depth=true,viewer=view_method)
}}}
{{attachment:3D_Limit_Defn.png}}


{{{#!sagecell

## An interactive way to demonstrate limits of multivariate functions of the form z = f(x,y)
## This one uses contour plots and so will work with functions that have asymptotic behavior.
##
## John Travis
## Mississippi College
##
## Spring 2011
##

# An increasing number of contours for z = f(x,y) are utilized surrounding a desired (x_0,y_0).
# A limit can be shown to exist at (x_0,y_0) provided the point stays trapped between adjacent
# contour lines as the number of lines increases. If the contours change wildly near the point,
# then a limit does not exist.
# Looking for two different paths to approach (x_0,y_0) that utilize a different selection of colors
# will help locate paths to use that exhibit the absence of a limit.

var('x,y,z,u')
@interact(layout=dict(top=[['f'],['x0'],['y0']],
bottom=[['N'],['R']]))
def _(f=input_box(default=(x*y^2)/(x^2+y^4),width=30,label='$f(x)$'),
        N=slider(5,100,1,10,label='Number of Contours'),
        R=slider(0.1,1,0.01,1,label='Radius of circular neighborhood'),
        x0=input_box(0,width=10,label='$x_0$'),
        y0=input_box(0,width=10,label='$y_0$')):

    pretty_print(html('Enter $(x_0 ,y_0 )$ above and see what happens as the number of contour levels $\\rightarrow \infty $.'))
    pretty_print(html('A surface will have a limit in the center of this graph provided there is not a sudden change in color there.'))

# Need to make certain the min and max contour lines are not huge due to asymptotes. If so, clip and start contours at some reasonable
# values so that there are a nice collection of contours to show around the desired point.

    surface = contour_plot(f,(x,x0-1,x0+1),(y,y0-1,y0+1),cmap=True,colorbar=True,fill=False,contours=N)
    surface += parametric_plot([R*cos(u),R*sin(u)],[0,2*pi],color='black')
# Nice to use if f=x*y^2/(x^2 + y^4)
# var('u')
# surface += parametric_plot([u^2,u],[u,-1,1],color='black')
    limit_point = point((x0,y0),color='red',size=30)
# show(limit_point+surface)
    pretty_print(table([[surface],['hi']]))
}}}
{{attachment:3D_Limit_Defn_Contours.png}}



== Directional Derivatives ==

This interact displays graphically a tangent line to a function, illustrating a directional derivative (the slope of the tangent line).

{{{#!sagecell
var('x,y,t,z')
f(x,y)=sin(x)*cos(y)

pif = float(pi)

line_thickness=3
surface_color='blue'
plane_color='purple'
line_color='red'
tangent_color='green'
gradient_color='orange'

@interact
def myfun(location=input_grid(1, 2, default=[0,0], label = "Location (x,y)", width=2), angle=slider(0, 2*pif, label = "Angle"),
show_surface=("Show surface", True)):
    location3d = vector(location[0]+[0])
    location = location3d[0:2]
    direction3d = vector(RDF, [cos(angle), sin(angle), 0])
    direction=direction3d[0:2]
    cos_angle = math.cos(angle)
    sin_angle = math.sin(angle)
    df = f.gradient()
    direction_vector=line3d([location3d, location3d+direction3d], arrow_head=True, rgbcolor=line_color, thickness=line_thickness)
    curve_point = (location+t*direction).list()
    curve = parametric_plot(curve_point+[f(*curve_point)], (t,-3,3),color=line_color,thickness=line_thickness)
    plane = parametric_plot((cos_angle*x+location[0],sin_angle*x+location[1],t), (x, -3,3), (t,-3,3),opacity=0.8, color=plane_color)
    pt = point3d(location3d.list(),color='green', size=10)

    tangent_line = parametric_plot((location[0]+t*cos_angle, location[1]+t*sin_angle, f(*location)+t*df(*location)*(direction)), (t, -3,3), thickness=line_thickness, color=tangent_color)
    picture3d = direction_vector+curve+plane+pt+tangent_line

    picture2d = contour_plot(f(x,y), (x,-3,3),(y,-3,3), plot_points=100)
    picture2d += arrow(location.list(), (location+direction).list())
    picture2d += point(location.list(),rgbcolor='green',pointsize=40)
    if show_surface:
        picture3d += plot3d(f, (x,-3,3),(y,-3,3),opacity=0.7)
        
    dff = df(location[0], location[1])
    dff3d = vector(RDF,dff.list()+[0])
    picture3d += line3d([location3d, location3d+dff3d], arrow_head=True, rgbcolor=gradient_color, thickness=line_thickness)
    picture2d += arrow(location.list(), (location+dff).list(), rgbcolor=gradient_color, width=line_thickness)
    show(picture3d,aspect=[1,1,1], axes=True)
    show(picture2d, aspect_ratio=1)
}}}
{{attachment:directional derivative.png}}

== 3D graph with points and curves ==
By Robert Marik

This sagelet is handy when showing local, constrained and absolute maxima and minima in two variables.
Available as a [[http://user.mendelu.cz/marik/sage/3Dgraph_with_points.sws|worksheet]]

{{{#!sagecell
x,y, t, u, v =var('x y t u v')
INI_func='x^2-2*x+y^2-2*y'
INI_box='-1,3.2,-1,3.2'
INI_points='(1,1,\'green\'),(3/2,3/2),(0,1),(1,0),(0,0,\'black\'),(3,0,\'black\'),(0,3,\'black\')'
INI_curves='(t,0,0,3,\'red\'),(0,t,0,3,\'green\'),(t,3-t,0,3)'
@interact
def _(func=input_box(INI_func,label="f(x,y)=",type=str),\
  bounds=input_box(INI_box,label="xmin,xmax,ymin,ymax",type=str),\
  st_points=input_box(INI_points,\
  label="points <br><small><small>(comma separated pairs, optionally with color)</small></small>", type=str),\
  bnd_curves=input_box(INI_curves,label="curves on boundary<br> <small><small><i>(x(t),y(t),tmin,tmax,'opt_color')</i></small></small>", type=str),\
 show_planes=("Show zero planes", False), show_axes=("Show axes", True),
 show_table=("Show table", True)):
 f=sage_eval('lambda x,y: ' + func)
 pretty_print(html(r'Function $ f(x,y)=%s$ '%latex(f(x,y))))
 xmin,xmax,ymin,ymax=sage_eval('('+bounds+')')
 A=plot3d(f(x,y),(x,xmin,xmax),(y,ymin,ymax),opacity=0.5)
 if not(bool(st_points=='')):
     st_p=sage_eval('('+st_points+',)')
     html(r'<table border=1>')
     for current in range(len(st_p)):
         point_color='red'
         if bool(len(st_p[current])==3):
              point_color=st_p[current][2]
         x0=st_p[current][0]
         y0=st_p[current][1]
         z0=f(x0,y0)
         if show_table:
              pretty_print(html(r'<tr><td>$\quad f(%s,%s)\quad $</td><td>$\quad %s$</td>\
              </tr>'%(latex(x0),latex(y0),z0.n())))
         A=A+point3d((x0,y0,z0),size=9,rgbcolor=point_color)
     html(r'</table>')
 if not(bool(bnd_curves=='')):
     bnd_cc=sage_eval('('+bnd_curves+',)',locals={'t':t})
     for current in range(len(bnd_cc)):
         bnd_c=bnd_cc[current]+('black',)
         A=A+parametric_plot3d((bnd_c[0],bnd_c[1],f(bnd_c[0],bnd_c[1])),\
             (t,bnd_c[2],bnd_c[3]),thickness=3,rgbcolor=bnd_c[4])
 if show_planes:
     A=A+plot3d(0,(x,xmin,xmax),(y,ymin,ymax),opacity=0.3,rgbcolor='gray')
     zmax=A.bounding_box()[1][2]
     zmin=A.bounding_box()[0][2]
     A=A+parametric_plot3d((u,0,v),(u,xmin,xmax),(v,zmin,zmax),opacity=0.3,rgbcolor='gray')
     A=A+parametric_plot3d((0,u,v),(u,ymin,ymax),(v,zmin,zmax),opacity=0.3,rgbcolor='gray')
 if show_axes:
     zmax=A.bounding_box()[1][2]
     zmin=A.bounding_box()[0][2]
     A=A+line3d([(xmin,0,0), (xmax,0,0)], arrow_head=True,rgbcolor='black')
     A=A+line3d([(0,ymin,0), (0,ymax,0)], arrow_head=True,rgbcolor='black')
     A=A+line3d([(0,0,zmin), (0,0,zmax)], arrow_head=True,rgbcolor='black')
 show(A)
}}}

{{attachment:3Dgraph_with_points.png}}

== Approximating function in two variables by differential ==
by Robert Marik

{{{#!sagecell
x,y=var('x y')
html('<h2>Explaining approximation of a function in two \
variables by differential</h2>')
pretty_print(html('Points x0 and y0 are values where the exact value of the function \
is known. Deltax and Deltay are displacements of the new point. Exact value \
and approximation by differential at shifted point are compared.'))
@interact
def _(func=input_box('sqrt(x^3+y^3)',label="f(x,y)=",type=str), x0=1, y0=2, \
  deltax=slider(-1,1,0.01,0.2),\
  deltay=slider(-1,1,0.01,-0.4), xmin=0, xmax=2, ymin=0, ymax=3):
  f=sage_eval('lambda x,y: ' + func)
  derx(x,y)=diff(f(x,y),x)
  dery(x,y)=diff(f(x,y),y)
  tangent(x,y)=f(x0,y0)+derx(x0,y0)*(x-x0)+dery(x0,y0)*(y-y0)
  A=plot3d(f(x,y),(x,xmin,xmax),(y,ymin,ymax),opacity=0.5)
  B=plot3d(tangent(x,y),(x,xmin,xmax),(y,ymin,ymax),color='red',opacity=0.5)
  C=point3d((x0,y0,f(x0,y0)),rgbcolor='blue',size=9)
  CC=point3d((x0+deltax,y0+deltay,f(x0+deltax,y0+deltay)),rgbcolor='blue',size=9)
  D=point3d((x0+deltax,y0+deltay,tangent(x0+deltax,y0+deltay)),rgbcolor='red',size=9)
  exact_value_ori=f(x0,y0).n(digits=10)
  exact_value=f(x0+deltax,y0+deltay)
  approx_value=tangent(x0+deltax,y0+deltay).n(digits=10)
  abs_error=(abs(exact_value-approx_value))
  pretty_print(html(r'Function $ f(x,y)=%s \approx %s $ '%(latex(f(x,y)),latex(tangent(x,y)))))
  pretty_print(html(r' $f %s = %s$'%(latex((x0,y0)),latex(exact_value_ori))))
  pretty_print(html(r'Shifted point $%s$'%latex(((x0+deltax),(y0+deltay)))))
  pretty_print(html(r'Value of the function in shifted point is $%s$'%f(x0+deltax,y0+deltay)))
  pretty_print(html(r'Value on the tangent plane in shifted point is $%s$'%latex(approx_value)))
  pretty_print(html(r'Error is $%s$'%latex(abs_error)))
  show(A+B+C+CC+D)
}}}
{{attachment:3D_differential.png}}

== Taylor approximations in two variables ==
by John Palmieri

This displays the nth order Taylor approximation, for n from 1 to 10, of the function sin(x^2^ + y^2^) cos(y) exp(-(x^2^+y^2^)/2).
{{{#!sagecell
var('x y')
var('xx yy')
G = sin(xx^2 + yy^2) * cos(yy) * exp(-0.5*(xx^2+yy^2))
def F(x,y):
    return G.subs(xx=x).subs(yy=y)
plotF = plot3d(F, (0.4, 2), (0.4, 2), adaptive=True, color='blue')
@interact
def _(x0=(0.5,1.5), y0=(0.5, 1.5),
      order=(1..10)):
    F0 = float(G.subs(xx=x0).subs(yy=y0))
    P = (x0, y0, F0)
    dot = point3d(P, size=15, color='red')
    plot = dot + plotF
    approx = F0
    for n in range(1, order+1):
        for i in range(n+1):
            if i == 0:
                deriv = G.diff(yy, n)
            elif i == n:
                deriv = G.diff(xx, n)
            else:
                deriv = G.diff(xx, i).diff(yy, n-i)
            deriv = float(deriv.subs(xx=x0).subs(yy=y0))
            coeff = binomial(n, i)/factorial(n)
            approx += coeff * deriv * (x-x0)^i * (y-y0)^(n-i)
    plot += plot3d(approx, (x, 0.4, 1.6),
             (y, 0.4, 1.6), color='red', opacity=0.7)
    pretty_print(html('$F(x,y) = e^{-(x^2+y^2)/2} \\cos(y) \\sin(x^2+y^2)$'))
    show(plot)
}}}
{{attachment:taylor-3d.png}}


== Volumes over non-rectangular domains ==

by John Travis

https://cloud.sagemath.com/projects/19575ea0-317e-402b-be57-368d04c113db/files/pub/2801-2901/2829.sagews

{{{#!sagecell
## Graphing surfaces over non-rectangular domains
## John Travis
## Spring 2011
##
##
## An updated version of this worksheet may be available at http://sagenb.mc.edu
##
## Interact allows the user to input up to two inequality constraints on the
## domain when dealing with functional surfaces
##
## User inputs:
## f = "top" surface with z = f(x,y)
## g = "bottom" surface with z = g(x,y)
## condition1 = a single boundary constraint. It should not include && or | to join two conditions.
## condition2 = another boundary constraint. If there is only one constraint, just enter something true
## or even just an x (or y) in the entry blank.
##
##

var('x,y')

# f is the top surface
# g is the bottom surface
global f,g

# condition1 and condition2 are the inequality constraints. It would be nice
# to have any number of conditions connected by $$ or |
global condition1,condition2

@interact
def _(f=input_box(default=(1/3)*x^2 + (1/4)*y^2 + 5,label='$f(x)=$'),
        g=input_box(default=-1*x+0*y,label='$g(x)=$'),
        condition1=input_box(default= x^2+y^2<8,label='$Constraint_1=$'),
        condition2=input_box(default=y<sin(3*x),label='$Constraint_2=$'),
        show_3d=('Stereographic',false), show_vol=('Shade volume',true),
        dospin = ('Spin?',true),
        clr = color_selector('#faff00', label='Volume Color', widget='colorpicker', hide_box=True),
        xx = range_slider(-5, 5, 1, default=(-3,3), label='X Range'),
        yy = range_slider(-5, 5, 1, default=(-3,3), label='Y Range'),
        auto_update=false):
    
    # This is the top function actually graphed by using NaN outside domain
    def F(x,y):
        if condition1(x=x,y=y):
            if condition2(x=x,y=y):
                return f(x=x,y=y)
            else:
                return -NaN
        else:
            return -NaN

    # This is the bottom function actually graphed by using NaN outside domain
    def G(x,y):
        if condition1(x=x,y=y):
            if condition2(x=x,y=y):
                return g(x=x,y=y)
            else:
                return -NaN
        else:
            return -NaN
        
    P = Graphics()
      
# The graph of the top and bottom surfaces
    P_list = []
    P_list.append(plot3d(F,(x,xx[0],xx[1]),(y,yy[0],yy[1]),color='blue',opacity=0.9))
    P_list.append(plot3d(G,(x,xx[0],xx[1]),(y,yy[0],yy[1]),color='gray',opacity=0.9))
    
# Interpolate "layers" between the top and bottom if desired

    if show_vol:
        ratios = range(10)

        def H(x,y,r):
            return (1-r)*F(x=x,y=y)+r*G(x=x,y=y)
        P_list.extend([
        plot3d(lambda x,y: H(x,y,ratios[1]/10),(x,xx[0],xx[1]),(y,yy[0],yy[1]),opacity=0.2,color=clr),
        plot3d(lambda x,y: H(x,y,ratios[2]/10),(x,xx[0],xx[1]),(y,yy[0],yy[1]),opacity=0.2,color=clr),
        plot3d(lambda x,y: H(x,y,ratios[3]/10),(x,xx[0],xx[1]),(y,yy[0],yy[1]),opacity=0.2,color=clr),
        plot3d(lambda x,y: H(x,y,ratios[4]/10),(x,xx[0],xx[1]),(y,yy[0],yy[1]),opacity=0.2,color=clr),
        plot3d(lambda x,y: H(x,y,ratios[5]/10),(x,xx[0],xx[1]),(y,yy[0],yy[1]),opacity=0.2,color=clr),
        plot3d(lambda x,y: H(x,y,ratios[6]/10),(x,xx[0],xx[1]),(y,yy[0],yy[1]),opacity=0.2,color=clr),
        plot3d(lambda x,y: H(x,y,ratios[7]/10),(x,xx[0],xx[1]),(y,yy[0],yy[1]),opacity=0.2,color=clr),
        plot3d(lambda x,y: H(x,y,ratios[8]/10),(x,xx[0],xx[1]),(y,yy[0],yy[1]),opacity=0.2,color=clr),
        plot3d(lambda x,y: H(x,y,ratios[9]/10),(x,xx[0],xx[1]),(y,yy[0],yy[1]),opacity=0.2,color=clr)
        ])
# P = plot3d(lambda x,y: H(x,y,ratio/10),(x,xx[0],xx[1]),(y,yy[0],yy[1]),opacity=0.1)
             
           
# Now, accumulate all of the graphs into one grouped graph.
    P = sum(P_list[i] for i in range(len(P_list)))


    if show_3d:
        show(P,frame=true,axes=false,xmin=xx[0],xmax=xx[1],ymin=yy[0],ymax=yy[1],stereo='redcyan',figsize=(6,9),viewer='jmol',spin=dospin)
    else:
        show(P,frame=true,axes=false,xmin=xx[0],xmax=xx[1],ymin=yy[0],ymax=yy[1],figsize=(6,9),viewer='jmol',spin=dospin)
}}}
{{attachment:3D_Irregular_Volume.png}}

== Lateral Surface Area (FIXME in Jupyter) ==

by John Travis

http://sagenb.mc.edu/home/pub/89/

{{{#!sagecell
## Display and compute the area of the lateral surface between two surfaces
## corresponding to the (scalar) line integral
## John Travis
## Spring 2011
##

var('x,y,t,s')
@interact(layout=dict(top=[['f','u'],['g','v']],
left=[['a'],['b'],['in_3d'],['smoother']],
bottom=[['xx','yy']]))
def _(f=input_box(default=6-4*x^2-y^2*2/5,label='Top = $f(x,y) = $',width=30),
        g=input_box(default=-2+sin(x)+sin(y),label='Bottom = $g(x,y) = $',width=30),
        u=input_box(default=cos(t),label='   $ x = u(t) = $',width=20),
        v=input_box(default=2*sin(t),label='   $ y = v(t) = $',width=20),
        a=input_box(default=0,label='$a = $',width=10),
        b=input_box(default=3*pi/2,label='$b = $',width=10),
        xx = range_slider(-5, 5, 1, default=(-1,1), label='x view'),
        yy = range_slider(-5, 5, 1, default=(-2,2), label='y view'),
        in_3d = checkbox(default=true,label='3D'),
        smoother=checkbox(default=false),
        auto_update=true):
        
    ds = sqrt(derivative(u,t)^2+derivative(v,t)^2)
    
# Set up the integrand to compute the line integral, making all attempts
# to simplify the result so that it looks as nice as possible.
    A = (f(x=u,y=v)-g(x=u,y=v))*ds.simplify_trig().simplify()
    
# It is not expected that Sage can actually perform the line integral calculation.
# So, the result displayed may not be a numerical value as expected.
# Creating a good but harder example that "works" is desirable.
# If you want Sage to try, uncomment the lines below.

# line_integral = integrate(A,t,a,b)
# html(r'<align=center size=+1>Lateral Surface Area = $ %s $ </font>'%latex(line_integral))

    line_integral_approx = numerical_integral(A,a,b)[0]

    pretty_print(html(r'<font align=center size=+1>Lateral Surface $ \approx $ %s</font>'%str(line_integral_approx)))

# Plot the top function z = f(x,y) that is being integrated.
    G = plot3d(f,(x,xx[0],xx[1]),(y,yy[0],yy[1]),opacity=0.2)
    G += plot3d(g,(x,xx[0],xx[1]),(y,yy[0],yy[1]),opacity=0.2)

# Add space curves on the surfaces "above" the domain curve (u(t),v(t))
    G += parametric_plot3d([u,v,g(x=u,y=v)],(t,a,b),thickness=2,color='red')
    G += parametric_plot3d([u,v,f(x=u,y=v)],(t,a,b),thickness=2,color='red')
    k=0
    if smoother:
        delw = 0.025
        lat_thick = 3
    else:
        delw = 0.10
        lat_thick = 10
    for w in (a,a+delw,..,b):
        G += parametric_plot3d([u(t=w),v(t=w),s*f(x=u(t=w),y=v(t=w))+(1-s)*g(x=u(t=w),y=v(t=w))],(s,0,1),thickness=lat_thick,color='yellow',opacity=0.9)
        
    if in_3d:
        show(G,stereo='redcyan',spin=true)
    else:
        show(G,perspective_depth=true,spin=true)
}}}
{{attachment:Lateral_Surface.png}}


== Parametric surface example (FIXME in Jupyter) ==
by Marshall Hampton
{{{#!sagecell
var('u,v')
npi = RDF(pi)
@interact
def viewer(mesh = checkbox(default = False, label = 'Show u,v meshlines'), uc = slider(-2,2,1/10,0, label = '<span style="color:red">Constant u value</span>'), vc = slider(-2,2,1/10,0, label = '<span style="color:green">Constant v value</span>'), functions = input_box([u,v^2,u^2+v])):
    f1(u,v) = functions[0]
    f2(u,v) = functions[1]
    f3(u,v) = functions[2]
    surface_plot = parametric_plot3d([f1,f2,f3], (u,-2,2), (v,-2,2), mesh = mesh, opacity = .8)
    constant_u = line3d([[f1(uc,q), f2(uc,q), f3(uc,q)] for q in srange(-2,2,.01)], rgbcolor = (1,0,0), thickness = 3)
    constant_v = line3d([[f1(q,vc), f2(q,vc), f3(q,vc)] for q in srange(-2,2,.01)], rgbcolor = (0,1,0), thickness = 3)
    show(surface_plot + constant_u + constant_v, frame = False)
}}}
{{attachment:parametric_surface.png}}

== Line Integrals in 3D Vector Field ==

by John Travis

https://cloud.sagemath.com/projects/19575ea0-317e-402b-be57-368d04c113db/files/pub/2801-2901/2827-$%20%5Cint_%7BC%7D%20%5Cleft%20%5Clangle%20M,N,P%20%5Cright%20%5Crangle%20dr%20$%20=%20$%20%25s%20$.sagews

{{{#!sagecell
## This worksheet interactively computes and displays the line integral of a 3D vector field
## over a given smooth curve C
##
## John Travis
## Mississippi College
## 06/16/11
##
## An updated version of this worksheet may be available at http://sagenb.mc.edu
##

var('x,y,z,t,s')

@interact
def _(M=input_box(default=x*y*z,label="$M(x,y,z)$"),
        N=input_box(default=-y*z,label="$N(x,y,z)$"),
        P=input_box(default=z*y,label="$P(x,y,z)$"),
        u=input_box(default=cos(t),label="$x=u(t)$"),
        v=input_box(default=2*sin(t),label="$y=v(t)$"),
        w=input_box(default=t*(t-2*pi)/pi,label="$z=w(t)$"),
        tt = range_slider(-2*pi, 2*pi, pi/6, default=(0,2*pi), label='t Range'),
        xx = range_slider(-5, 5, 1, default=(-1,1), label='x Range'),
        yy = range_slider(-5, 5, 1, default=(-2,2), label='y Range'),
        zz = range_slider(-5, 5, 1, default=(-3,1), label='z Range'),
        in_3d=checkbox(true)):

# setup the parts and then compute the line integral
    dr = [derivative(u(t),t),derivative(v(t),t),derivative(w(t),t)]
    A = (M(x=u(t),y=v(t),z=w(t))*dr[0]
        +N(x=u(t),y=v(t),z=w(t))*dr[1]
        +P(x=u(t),y=v(t),z=w(t))*dr[2])
    global line_integral
    line_integral = integral(A(t=t),t,tt[0],tt[1])
    
    pretty_print(html(r'<h2 align=center>$ \int_{C} \left \langle M,N,P \right \rangle dr $ = $ %s $ </h2>'%latex(line_integral)))
    G = plot_vector_field3d((M,N,P),(x,xx[0],xx[1]),(y,yy[0],yy[1]),(z,zz[0],zz[1]),plot_points=6)
    G += parametric_plot3d([u,v,w],(t,tt[0],tt[1]),thickness='5',color='yellow')
    if in_3d:
        show(G,stereo='redcyan',spin=true)
    else:
        show(G,perspective_depth=true)
}}}
{{attachment:3D_Line_Integral.png}}

Sage Interactions - Calculus

goto interact main page

Contents

  1. Sage Interactions - Calculus
    1. Root Finding Using Bisection
    2. Newton's Method
    3. A contour map and 3d plot of two inverse distance functions
    4. A simple tangent line grapher
    5. Numerical integrals with the midpoint rule
    6. Numerical integrals with various rules
    7. Some polar parametric curves
    8. Function tool
    9. Newton-Raphson Root Finding
    10. Coordinate Transformations (FIXME in Jupyter)
    11. Taylor Series
    12. Illustration of the precise definition of a limit
    13. A graphical illustration of sin(x)/x -> 1 as x-> 0
    14. Quadric Surface Plotter
    15. The midpoint rule for numerically integrating a function of two variables
    16. Gaussian (Legendre) quadrature
    17. Vector Calculus, 2-D Motion
    18. Vector Calculus, 3-D Motion (FIXME)
    19. Multivariate Limits by Definition
    20. Directional Derivatives
    21. 3D graph with points and curves
    22. Approximating function in two variables by differential
    23. Taylor approximations in two variables
    24. Volumes over non-rectangular domains
    25. Lateral Surface Area (FIXME in Jupyter)
    26. Parametric surface example (FIXME in Jupyter)
    27. Line Integrals in 3D Vector Field

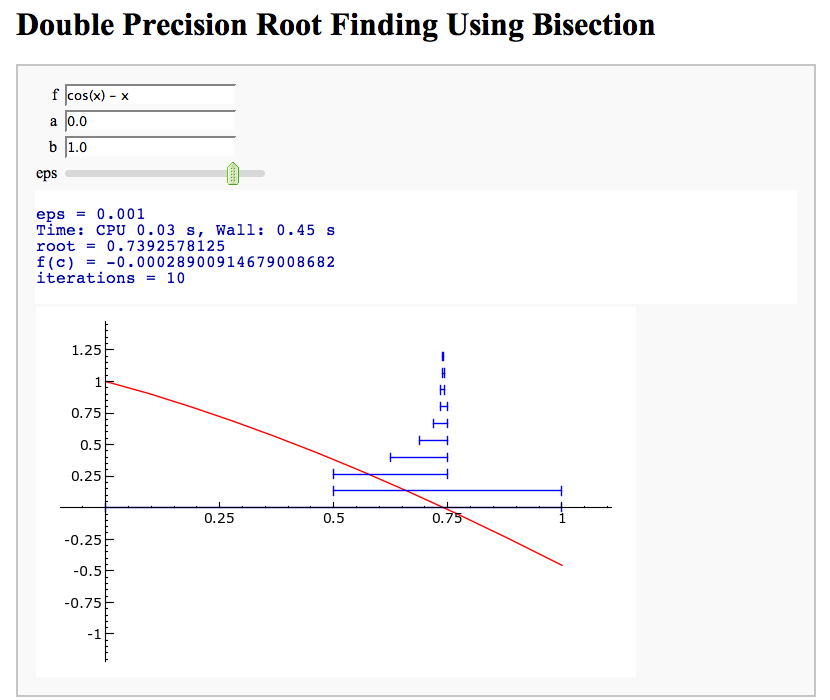
Root Finding Using Bisection

by William Stein

bisect.png

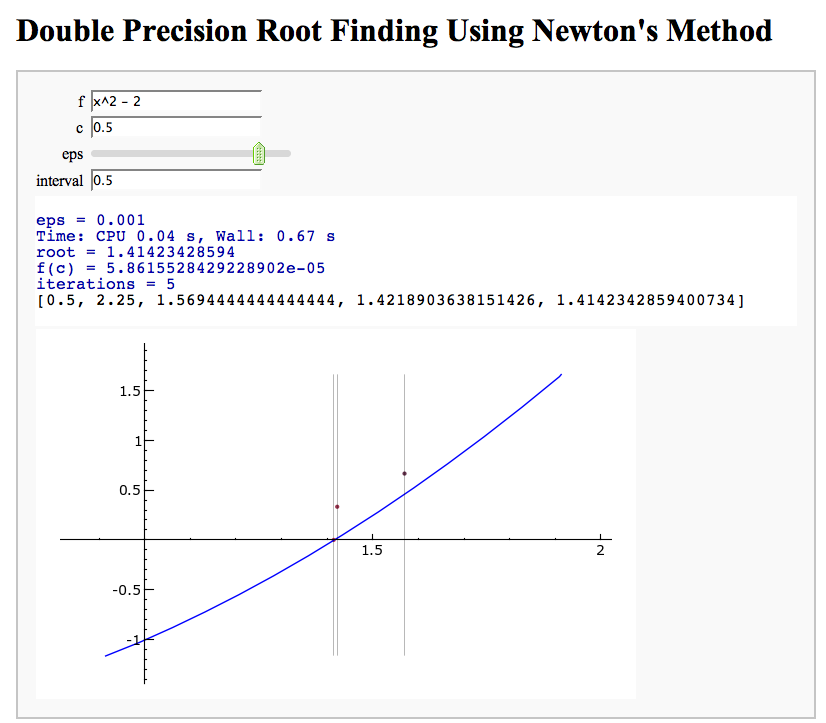
Newton's Method

Note that there is a more complicated Newton's method below.

by William Stein

https://cloud.sagemath.com/projects/19575ea0-317e-402b-be57-368d04c113db/files/pub/2801-2901/2824-Double%20Precision%20Root%20Finding%20Using%20Newton's%20Method.sagews

newton.png

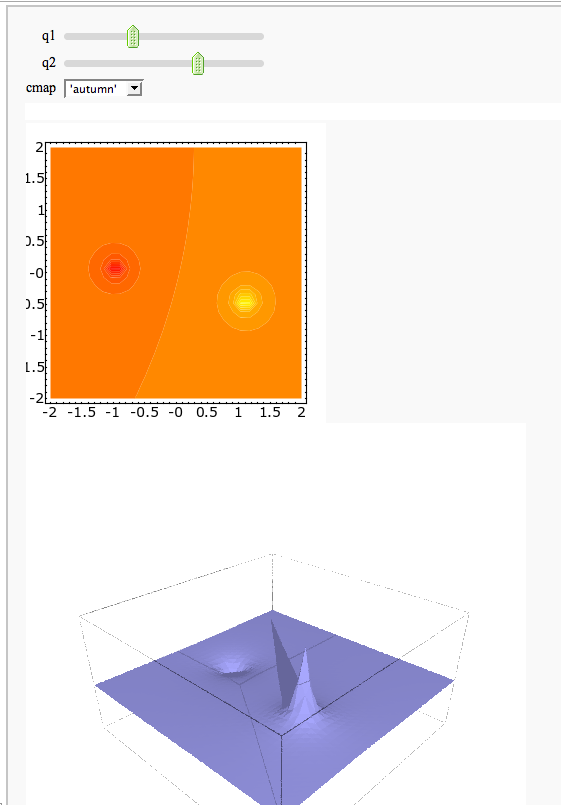
A contour map and 3d plot of two inverse distance functions

by William Stein

https://cloud.sagemath.com/projects/19575ea0-317e-402b-be57-368d04c113db/files/pub/2801-2901/2823.sagews

mountains.png

A simple tangent line grapher

by Marshall Hampton

tangents.png

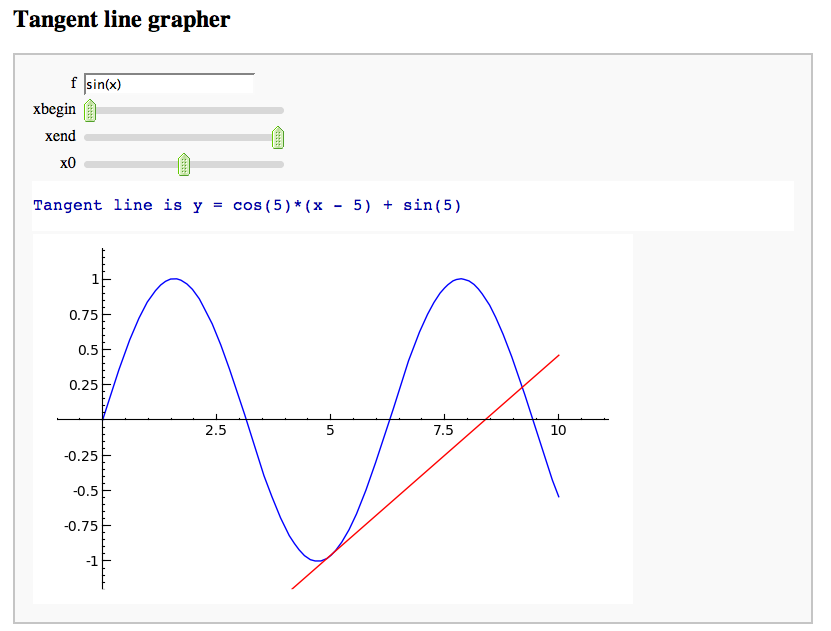
Numerical integrals with the midpoint rule

by Marshall Hampton

num_int.png

Numerical integrals with various rules

by Nick Alexander (based on the work of Marshall Hampton)

num_int2.png

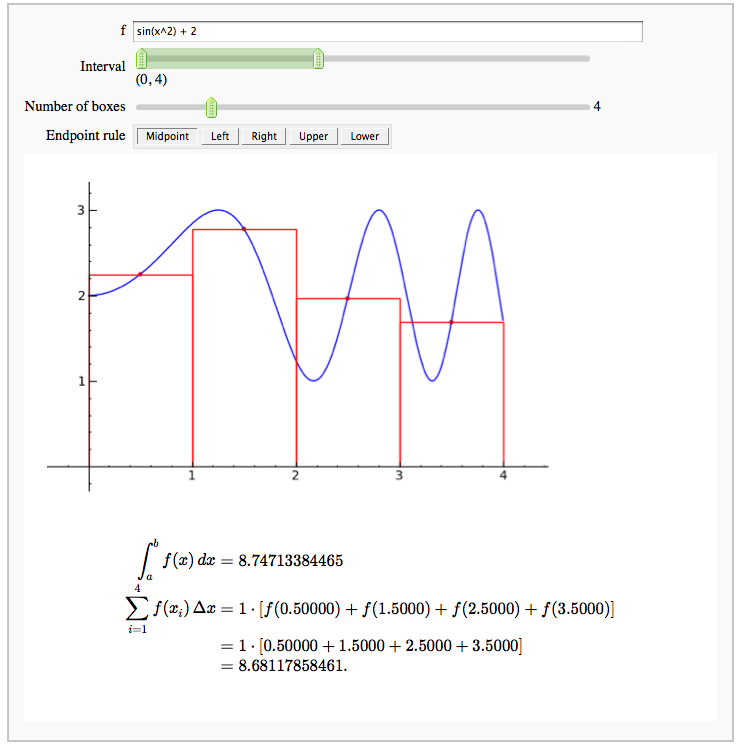
Some polar parametric curves

by Marshall Hampton. This is not very general, but could be modified to show other families of polar curves.

polarcurves1.png

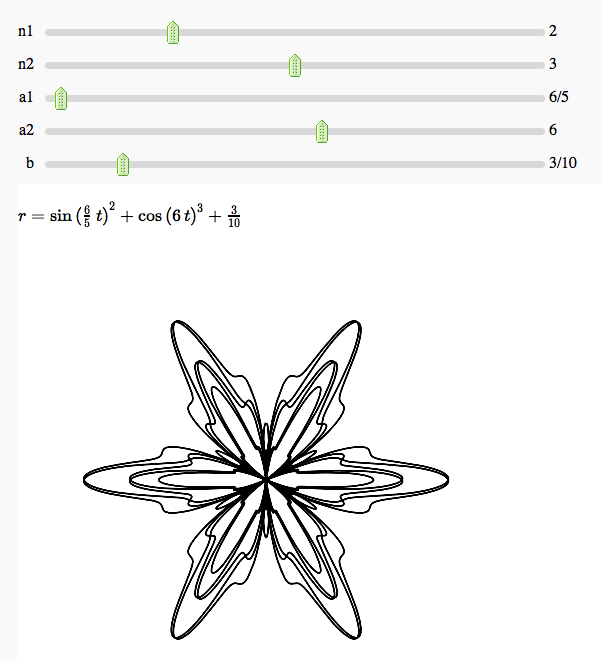
Function tool

Enter symbolic functions f, g, and a, a range, then click the appropriate button to compute and plot some combination of f, g, and a along with f and g. This is inspired by the Matlab funtool GUI.

funtool.png

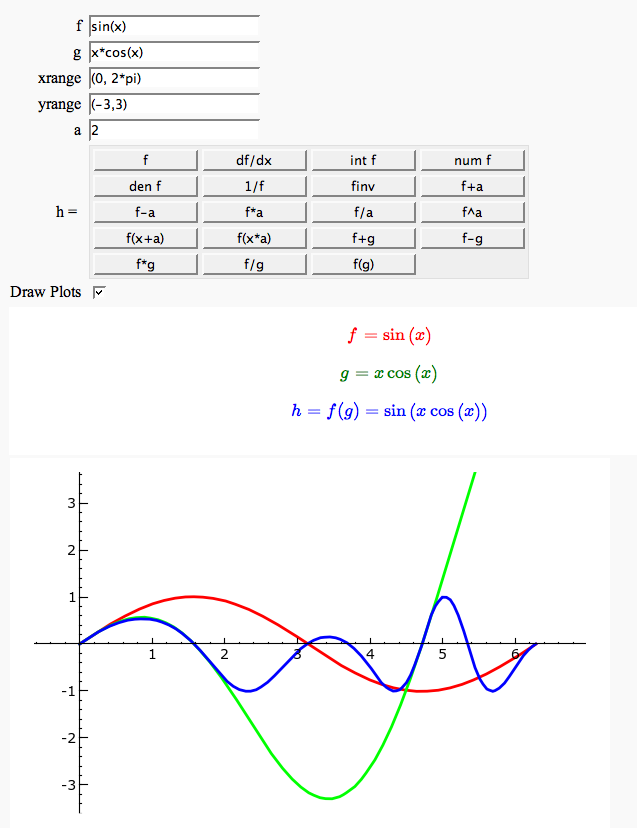
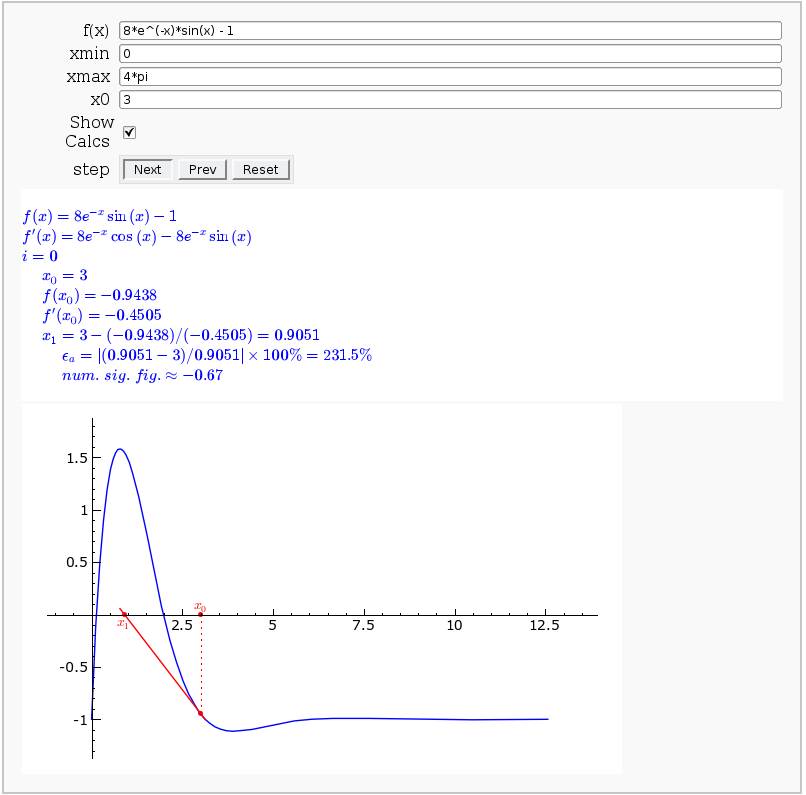
Newton-Raphson Root Finding

by Neal Holtz

This allows user to display the Newton-Raphson procedure one step at a time. It uses the heuristic that, if any of the values of the controls change, then the procedure should be re-started, else it should be continued.

newtraph.png

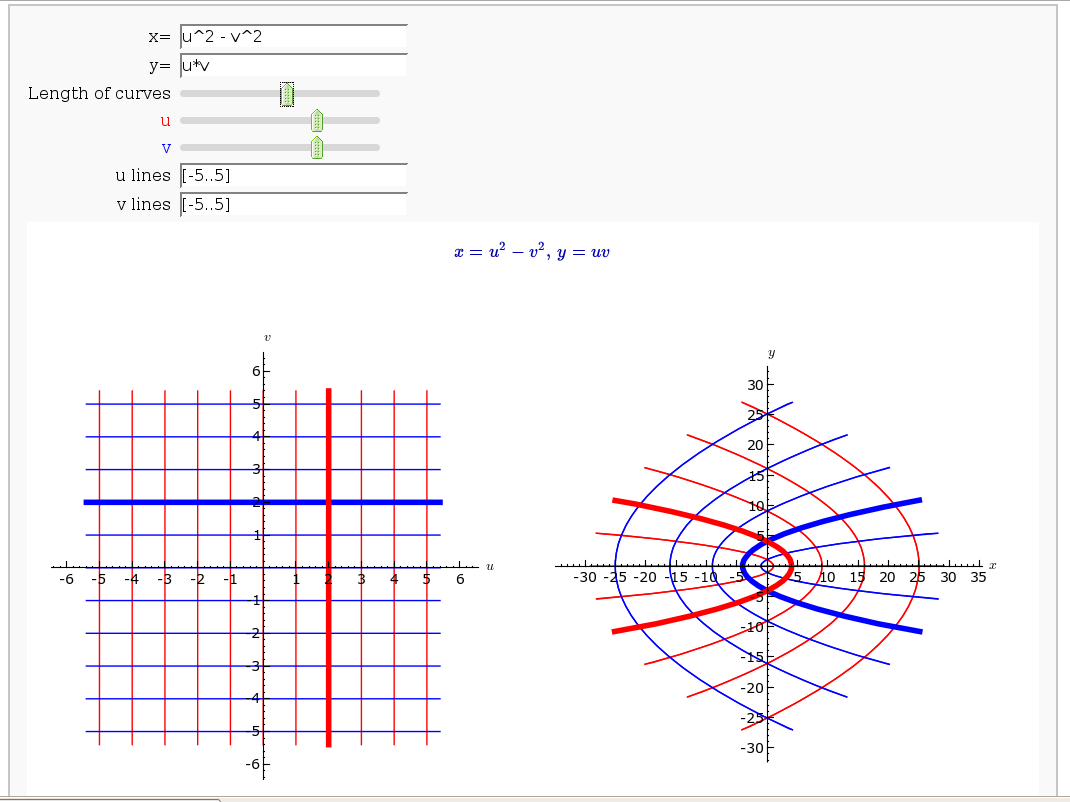
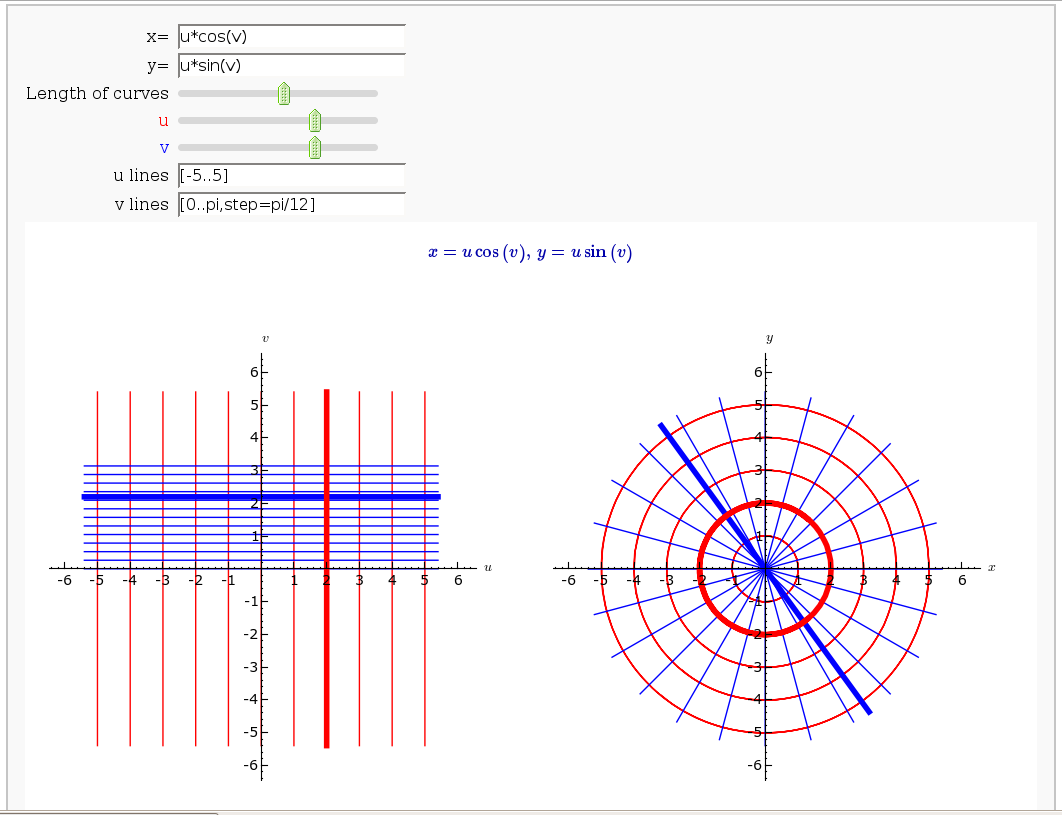
Coordinate Transformations (FIXME in Jupyter)

by Jason Grout

coordinate-transform-1.png coordinate-transform-2.png

Taylor Series

by Harald Schilly

taylor_series_animated.gif

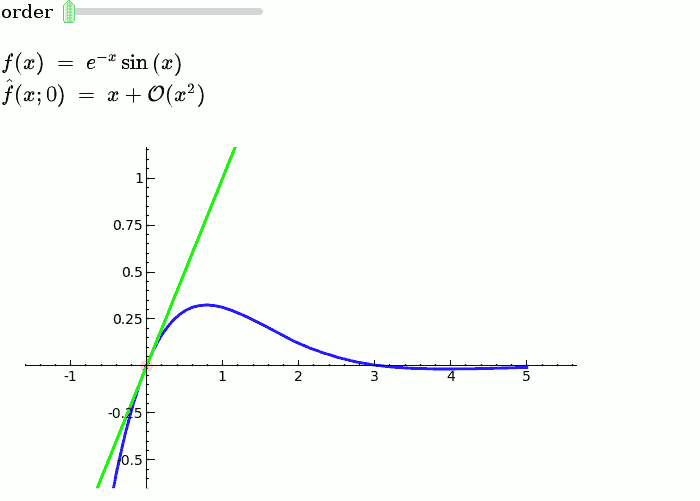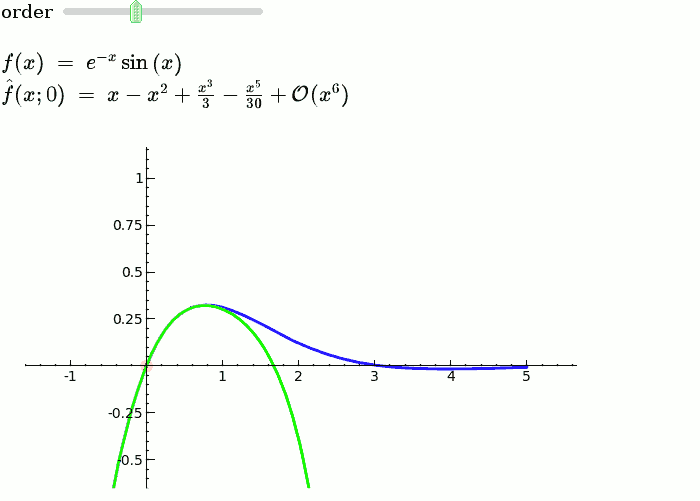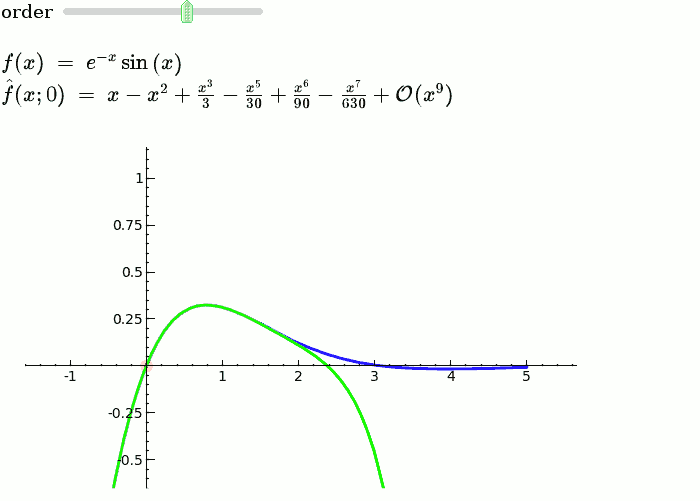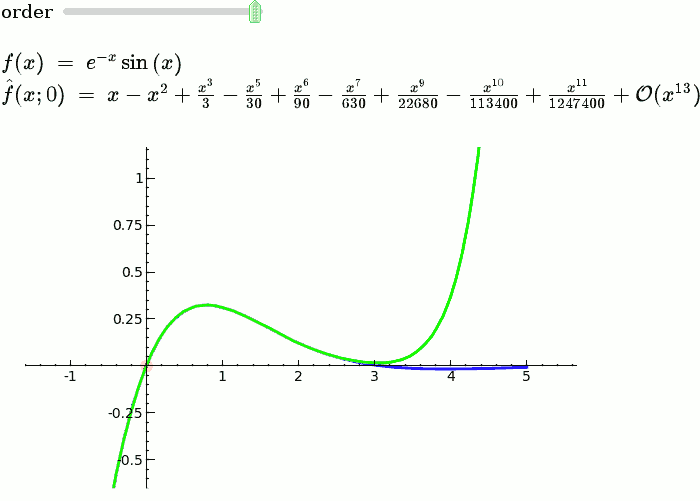
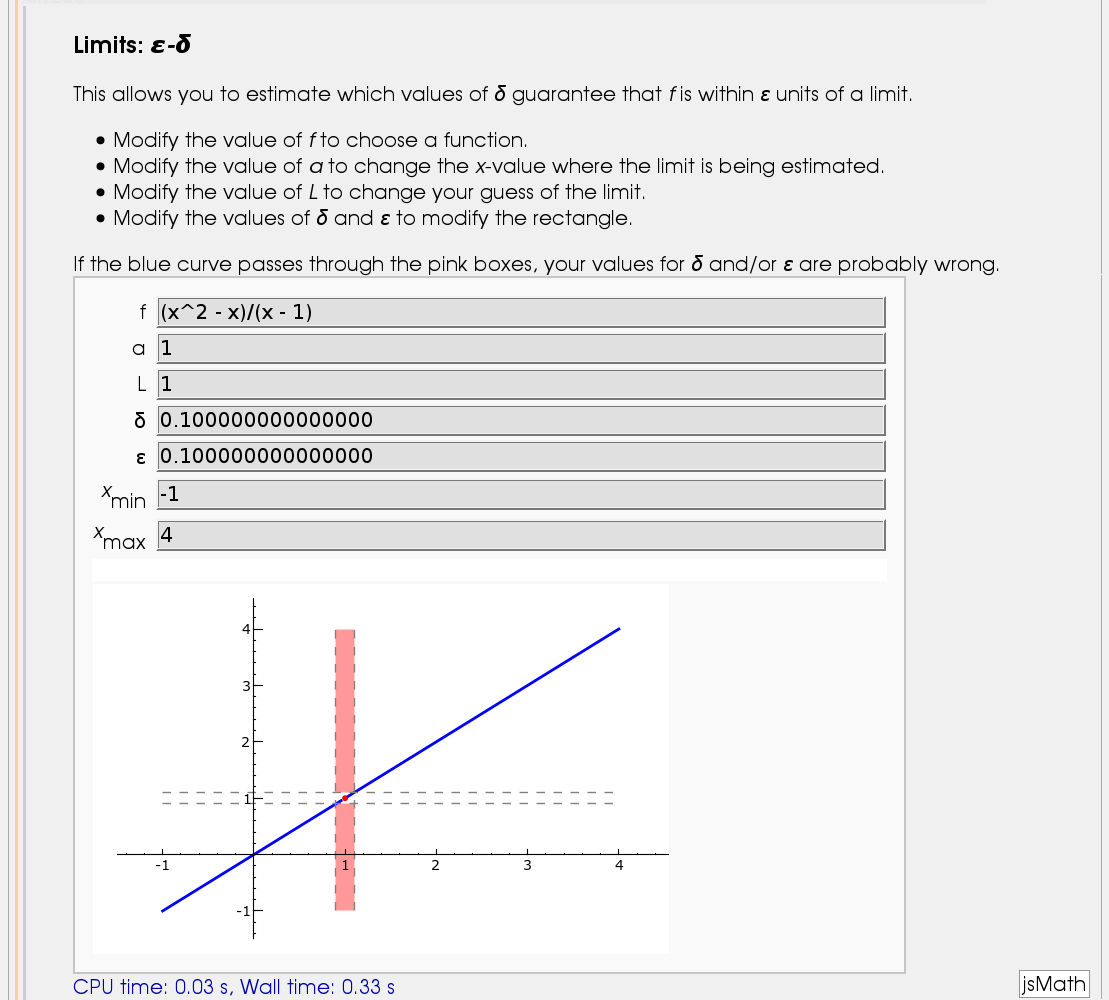
Illustration of the precise definition of a limit

by John Perry

I'll break tradition and put the image first. Apologies if this is Not A Good Thing.

snapshot_epsilon_delta.png

A graphical illustration of sin(x)/x -> 1 as x-> 0

by Wai Yan Pong

sinelimit.png

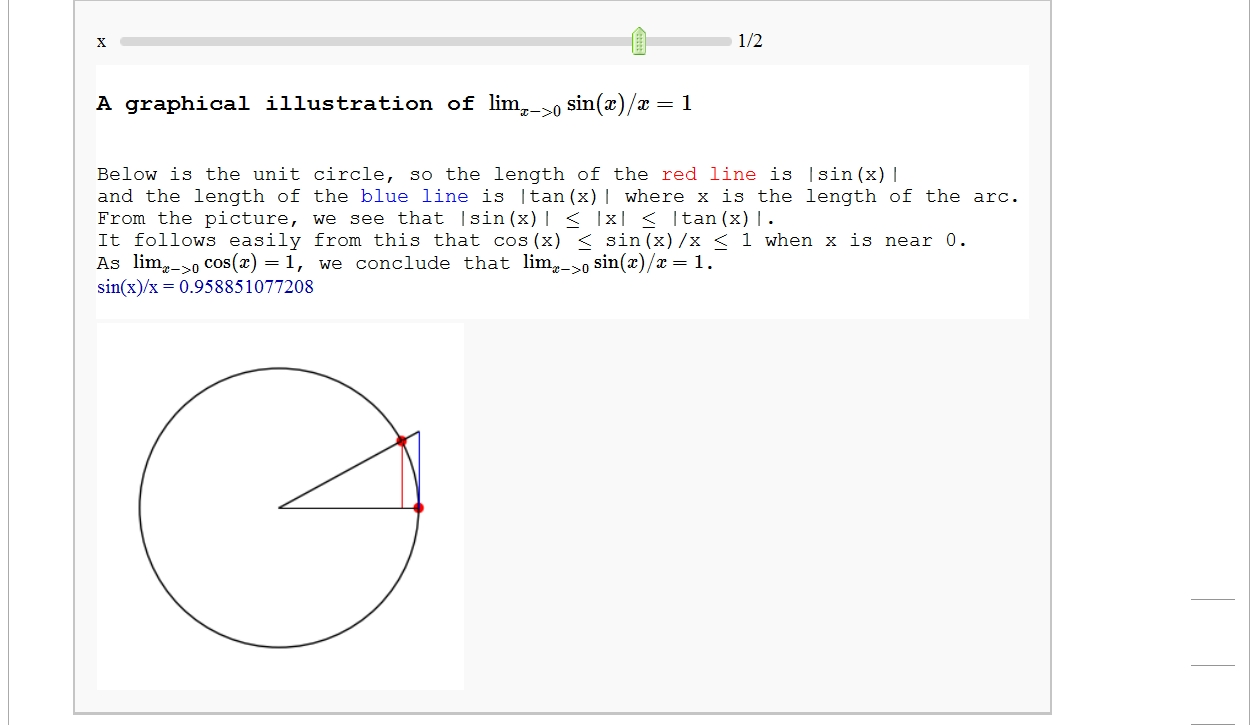
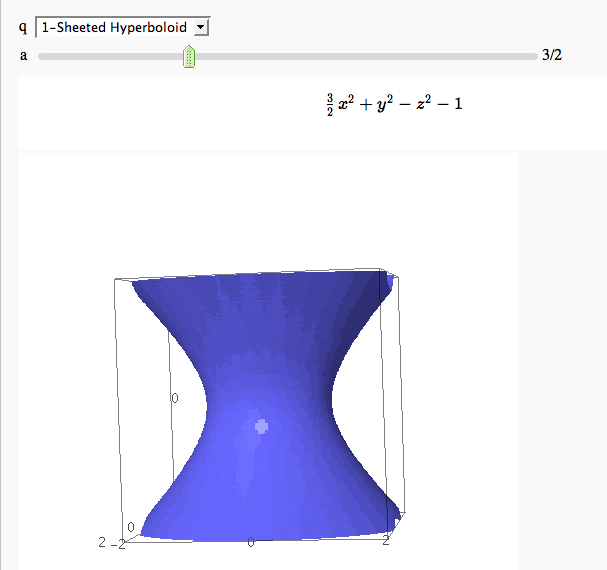
Quadric Surface Plotter

by Marshall Hampton. This is pretty simple, so I encourage people to spruce it up. In particular, it isn't set up to show all possible types of quadrics.

quadrics.png

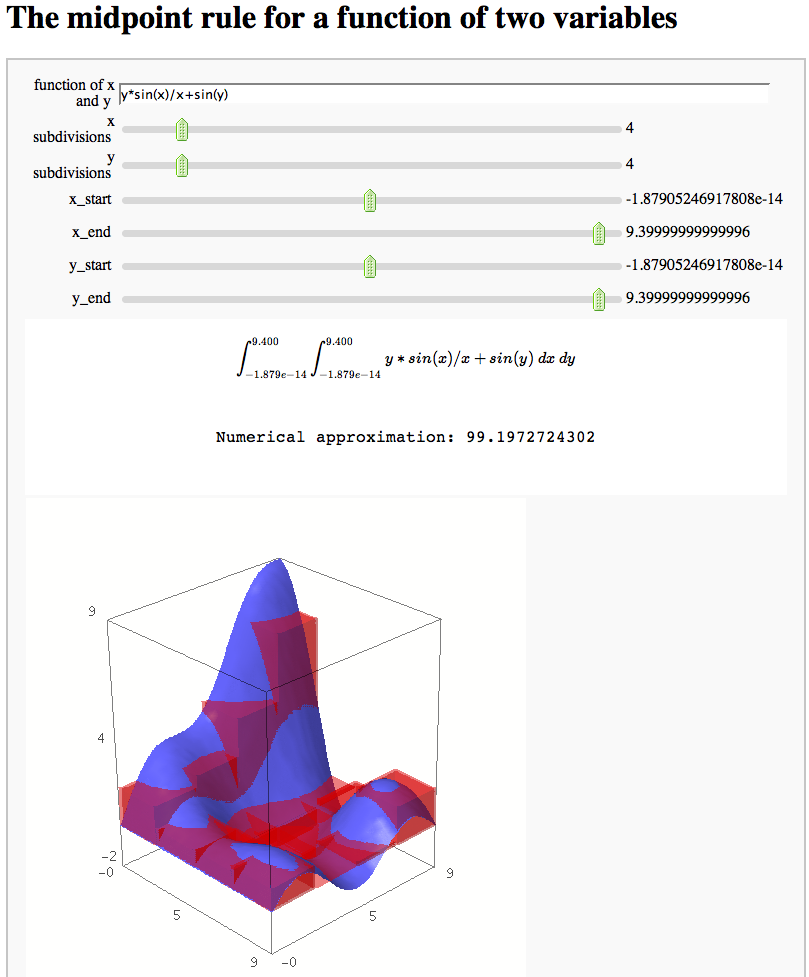
The midpoint rule for numerically integrating a function of two variables

by Marshall Hampton

numint2d.png

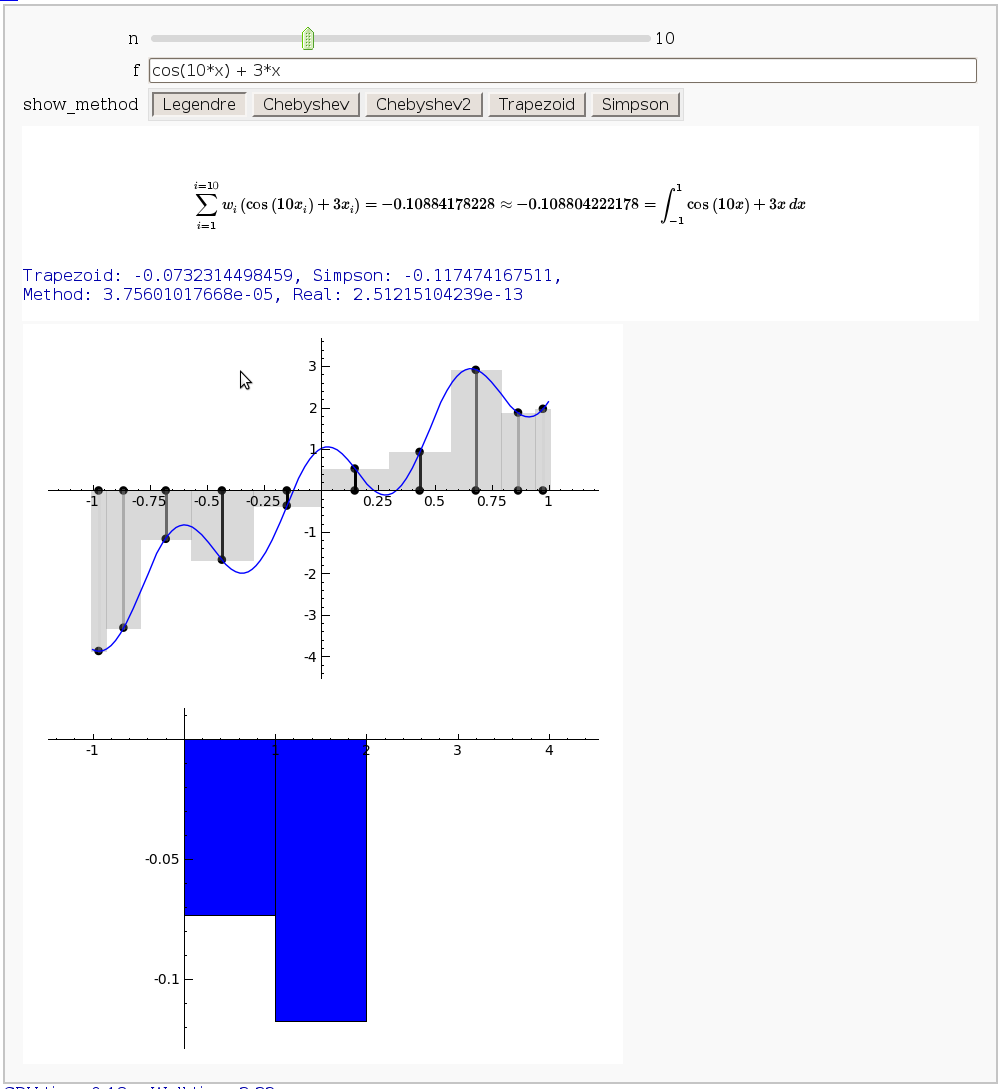
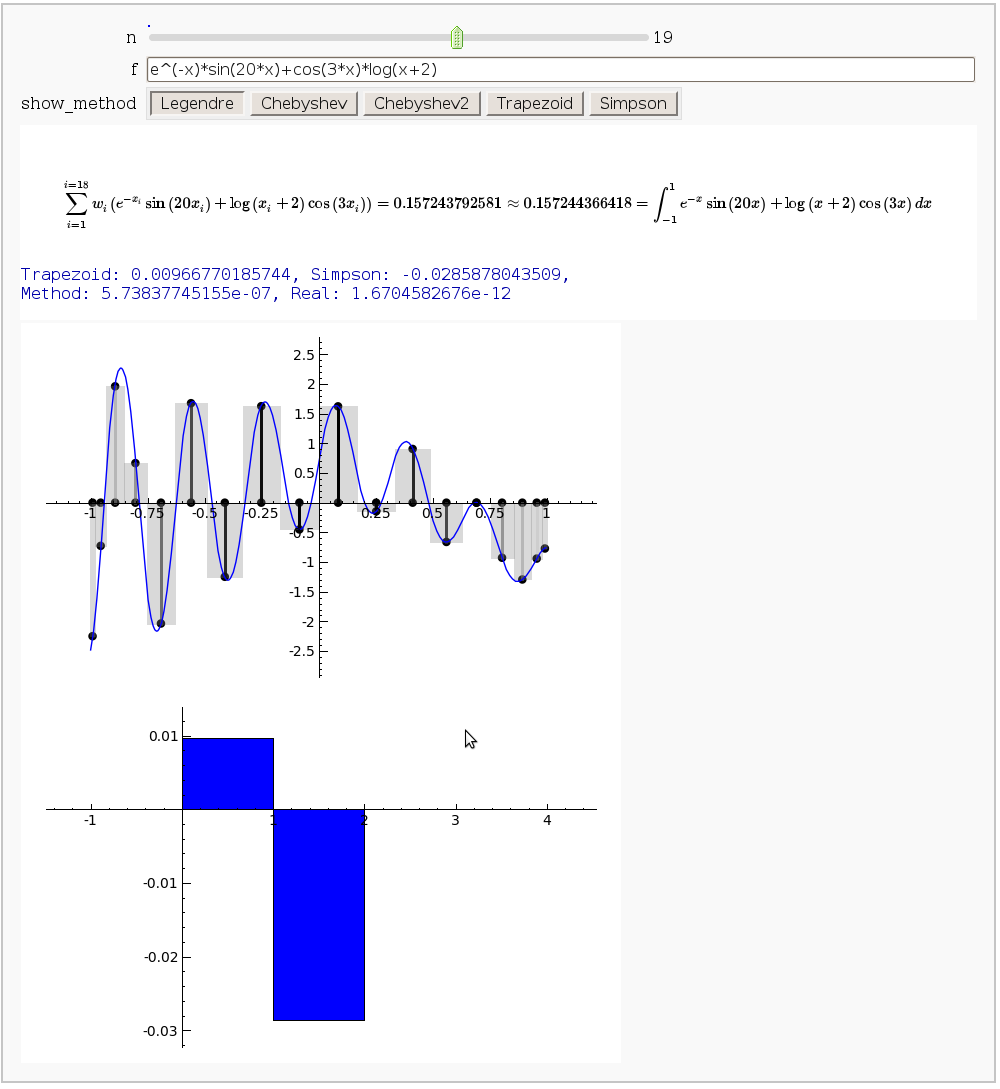
Gaussian (Legendre) quadrature

by Jason Grout

The output shows the points evaluated using Gaussian quadrature (using a weight of 1, so using Legendre polynomials). The vertical bars are shaded to represent the relative weights of the points (darker = more weight). The error in the trapezoid, Simpson, and quadrature methods is both printed out and compared through a bar graph. The "Real" error is the error returned from scipy on the definite integral.

quadrature1.png quadrature2.png

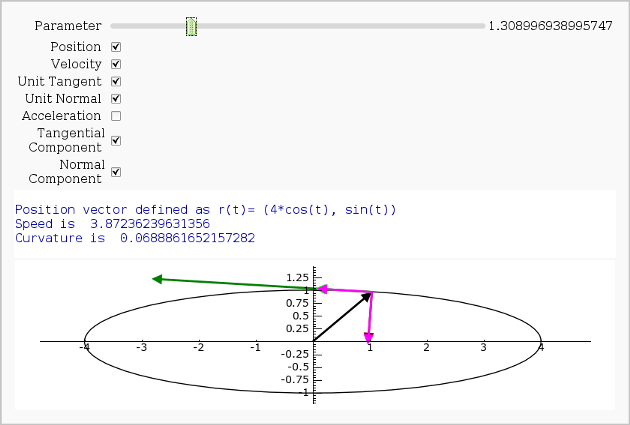
Vector Calculus, 2-D Motion

By Rob Beezer

A fast_float() version is available in a worksheet

motion2d.png

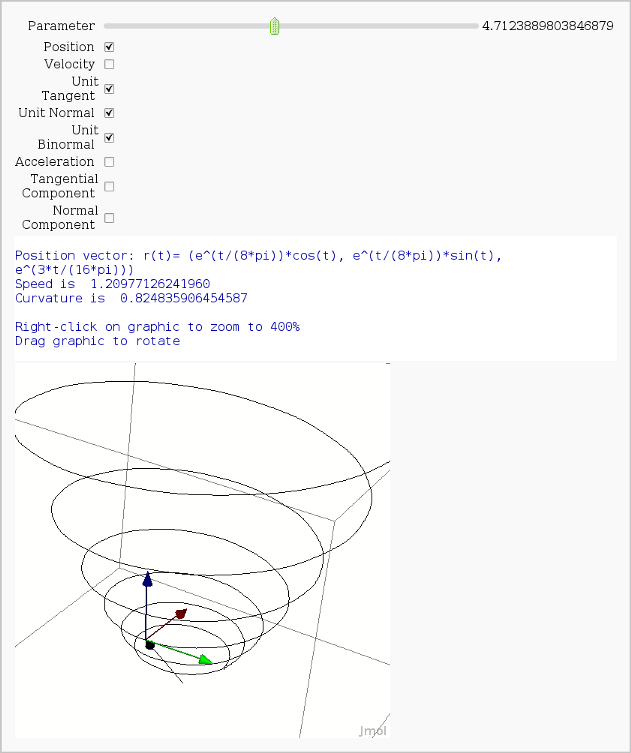
Vector Calculus, 3-D Motion (FIXME)

by Rob Beezer

Available as a worksheet

motion3d.png

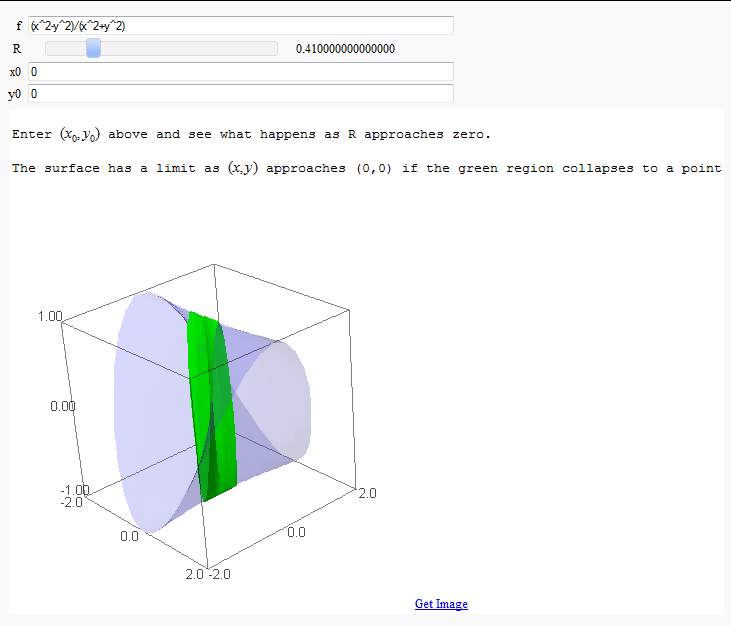
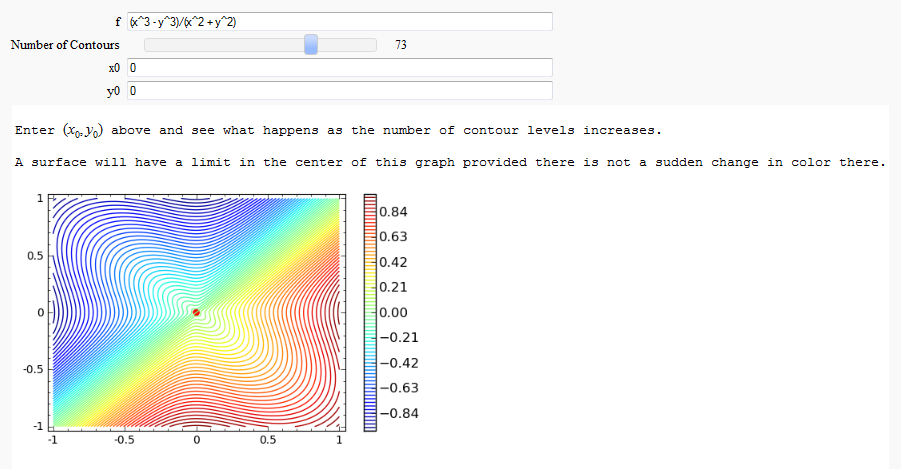
Multivariate Limits by Definition

by John Travis

http://sagenb.mc.edu/home/pub/97/

3D_Limit_Defn.png

3D_Limit_Defn_Contours.png

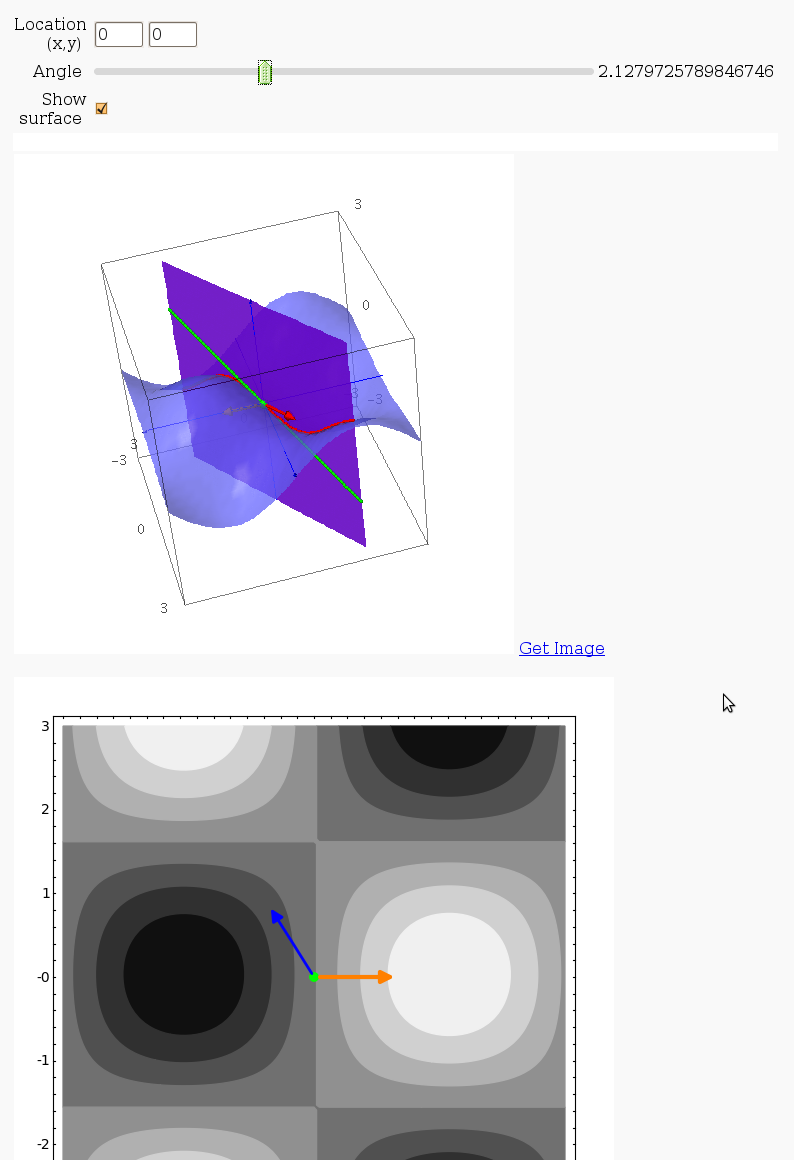
Directional Derivatives

This interact displays graphically a tangent line to a function, illustrating a directional derivative (the slope of the tangent line).

directional derivative.png

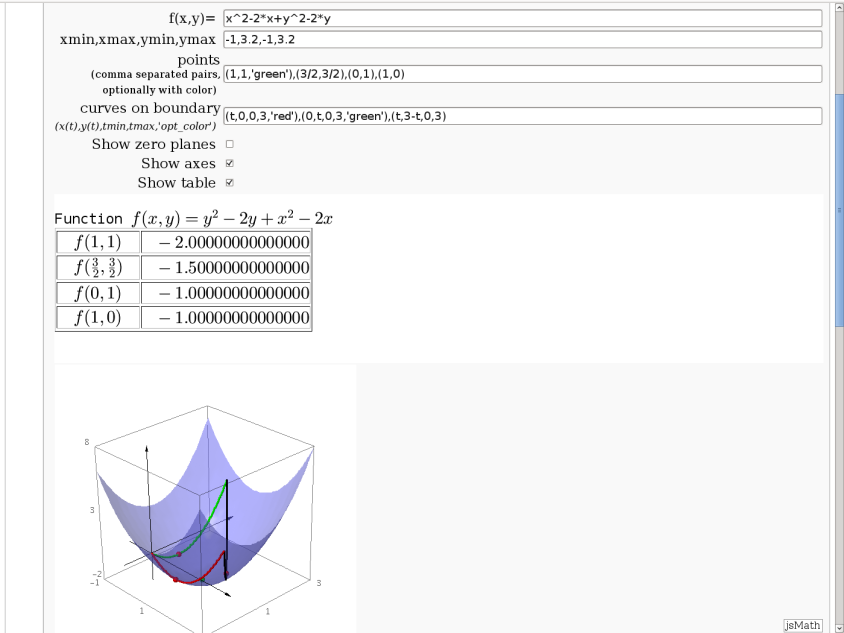
3D graph with points and curves

By Robert Marik

This sagelet is handy when showing local, constrained and absolute maxima and minima in two variables. Available as a worksheet

3Dgraph_with_points.png

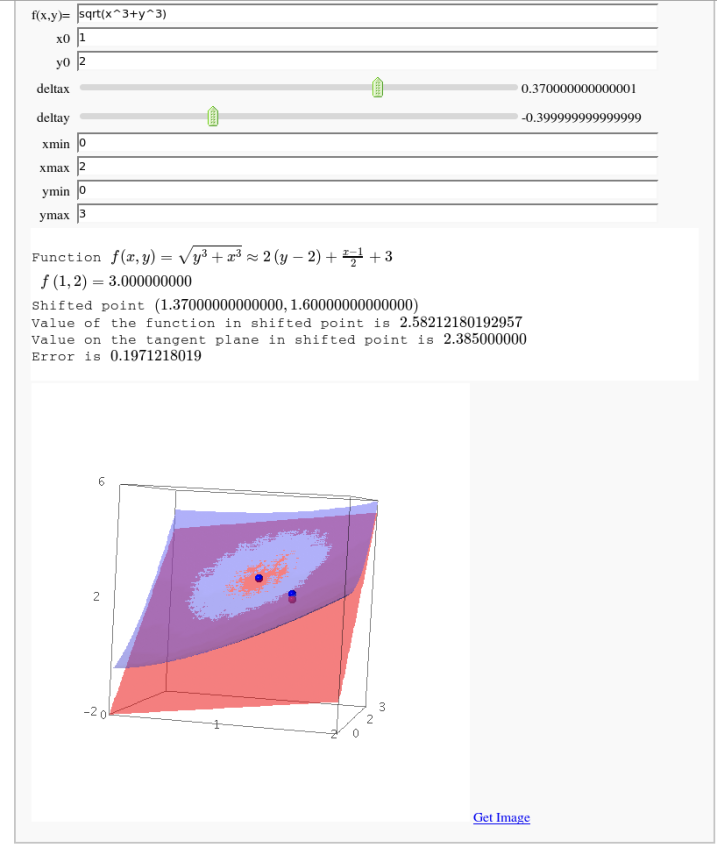
Approximating function in two variables by differential

by Robert Marik

3D_differential.png

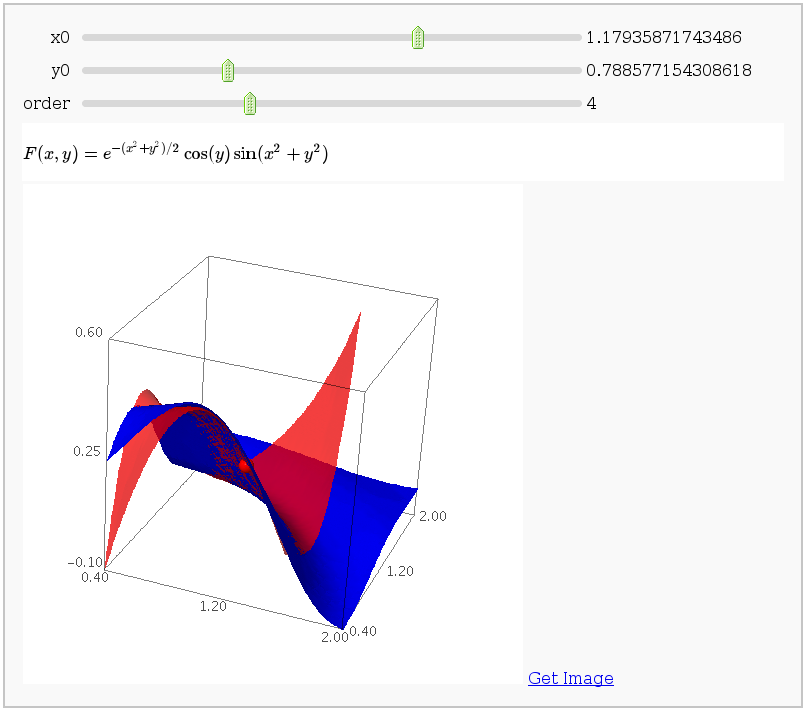
Taylor approximations in two variables

by John Palmieri

This displays the nth order Taylor approximation, for n from 1 to 10, of the function sin(x2 + y2) cos(y) exp(-(x2+y2)/2).

taylor-3d.png

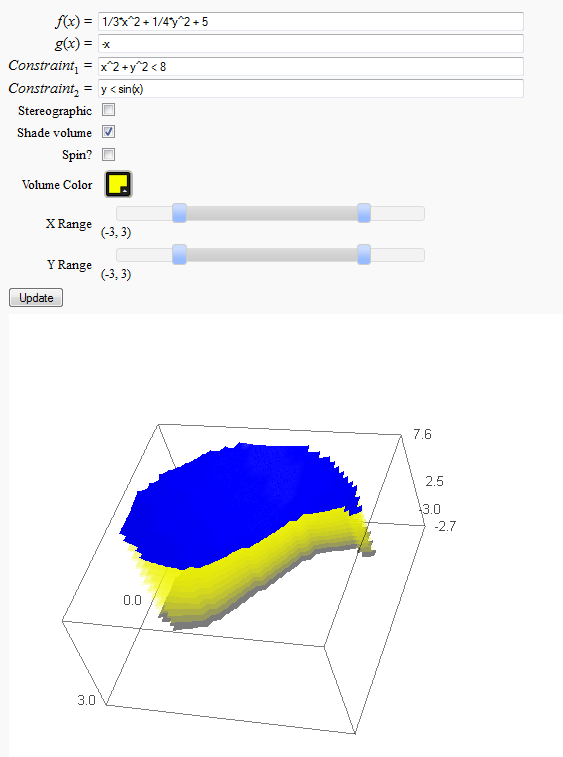
Volumes over non-rectangular domains

by John Travis

https://cloud.sagemath.com/projects/19575ea0-317e-402b-be57-368d04c113db/files/pub/2801-2901/2829.sagews

3D_Irregular_Volume.png

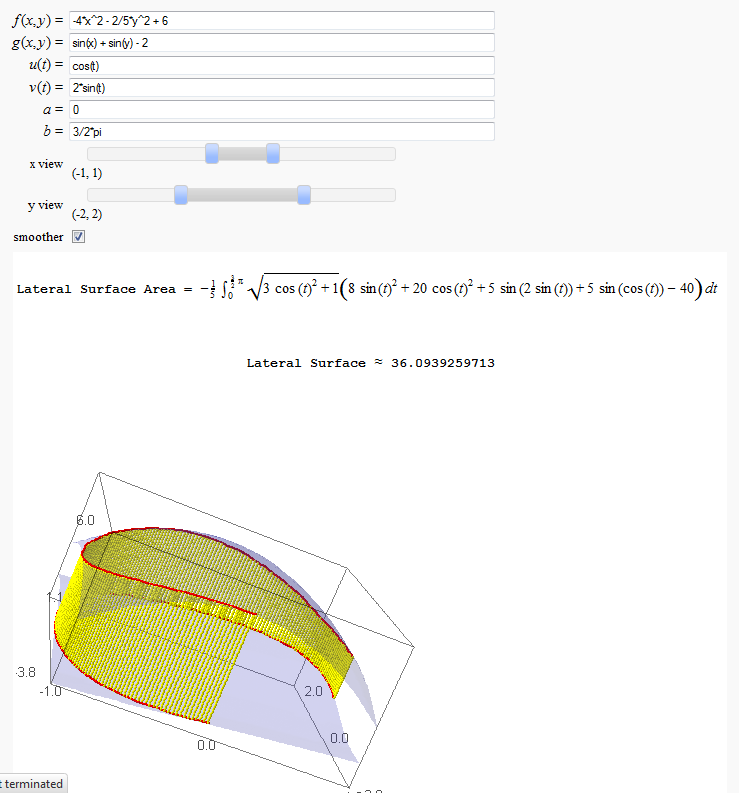
Lateral Surface Area (FIXME in Jupyter)

by John Travis

http://sagenb.mc.edu/home/pub/89/

Lateral_Surface.png

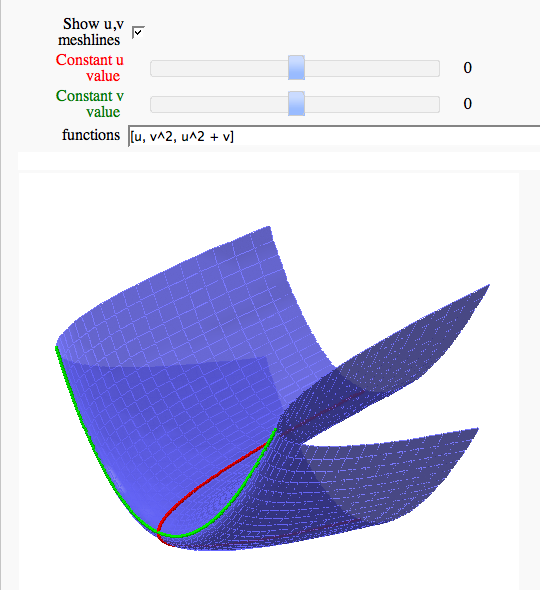
Parametric surface example (FIXME in Jupyter)

by Marshall Hampton

parametric_surface.png

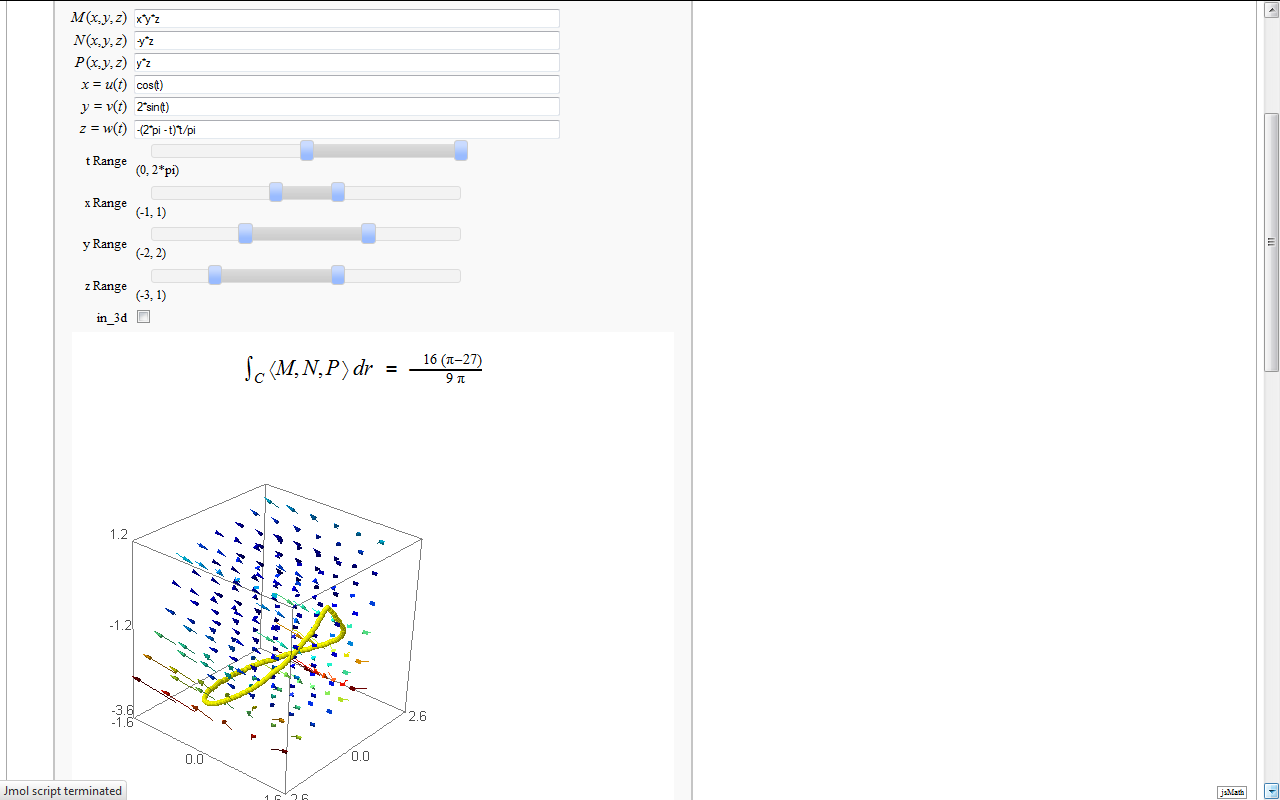
Line Integrals in 3D Vector Field

by John Travis

https://cloud.sagemath.com/projects/19575ea0-317e-402b-be57-368d04c113db/files/pub/2801-2901/2827-$%20%5Cint_%7BC%7D%20%5Cleft%20%5Clangle%20M,N,P%20%5Cright%20%5Crangle%20dr%20$%20=%20$%20%25s%20$.sagews

3D_Line_Integral.png

interact/calculus (last edited 2020-08-11 14:10:09 by kcrisman)