Differences between revisions 38 and 53 (spanning 15 versions)
⇤ ← Revision 38 as of 2011-06-16 18:10:11 →
Size: 45735
Editor: was
Comment:
← Revision 53 as of 2012-04-23 00:28:01 → ⇥
Size: 57675
Editor: rbeezer
Comment: Five derivatives now explicity with respect to t
Deletions are marked like this. Additions are marked like this.
Line 6: Line 6:
Line 9: Line 10:
{{{ {{{#!sagecell
Line 56: Line 57:
{{{ http://sagenb.org/home/pub/2824/

{{{#!sagecell
Line 72: Line 75:
     var('x')
Line 79: Line 84:
     print "f(c) = %r"%f(z)      print "f(c) = %r"%f(x=z)
Line 83: Line 88:
     P = plot(f, z-interval, z+interval, rgbcolor='blue')      P = plot(f, (x,z-interval, z+interval), rgbcolor='blue')
Line 96: Line 101:
{{{ {{{#!sagecell
Line 112: Line 117:
{{{ {{{#!sagecell
Line 132: Line 137:
{{{ {{{#!sagecell
Line 160: Line 165:
{{{ {{{#!sagecell
Line 233: Line 238:
{{{ {{{#!sagecell
Line 246: Line 251:
{{{ {{{#!sagecell
Line 344: Line 349:
{{{ {{{#!sagecell
Line 450: Line 455:
{{{ {{{#!sagecell
Line 492: Line 497:
{{{ {{{#!sagecell
Line 515: Line 520:
{{{ {{{#!sagecell
Line 542: Line 547:
{{{ {{{#!sagecell
Line 568: Line 573:
{{{ {{{#!sagecell
Line 583: Line 588:
{{{ {{{#!sagecell
Line 629: Line 634:
{{{
from scipy.special.orthogonal import p_roots		 {{{#!sagecell
import scipy
import numpy
from scipy.special.orthogonal import p_roots, t_roots, u_roots
Line 639: Line 646:
            'Chebyshev': {'w': 1/sqrt(1-x**2), 'xmin': -1, 'xmax': 1, 'func': t_roots},
                'Chebyshev2': {'w': sqrt(1-x**2), 'xmin': -1, 'xmax': 1, 'func': u_roots},
                'Trapezoid': {'w': 1, 'xmin': -1, 'xmax': 1, 'func': lambda n: (linspace(-1r,1,n), numpy.array([1.0r]+[2.0r]*(n-2)+[1.0r])*1.0r/n)},
                'Simpson': {'w': 1, 'xmin': -1, 'xmax': 1, 'func': lambda n: (linspace(-1r,1,n), numpy.array([1.0r]+[4.0r,2.0r]*int((n-3.0r)/2.0r)+[4.0r,1.0r])*2.0r/(3.0r*n))}}		      'Chebyshev': {'w': 1/sqrt(1-x**2), 'xmin': -1, 'xmax': 1, 'func': t_roots},
     'Chebyshev2': {'w': sqrt(1-x**2), 'xmin': -1, 'xmax': 1, 'func': u_roots},
     'Trapezoid': {'w': 1, 'xmin': -1, 'xmax': 1,          'func': lambda n: (linspace(-1r,1,n), numpy.array([1.0r]+[2.0r]*(n-2)+[1.0r])*1.0r/n)},
     'Simpson': {'w': 1, 'xmin': -1, 'xmax': 1,          'func': lambda n: (linspace(-1r,1,n),
            numpy.array([1.0r]+[4.0r,2.0r]*int((n-3.0r)/2.0r)+[4.0r,1.0r])*2.0r/(3.0r*n))}}
Line 646: Line 656:
    return polygon([(center-width2,0),(center+width2,0),(center+width2,height),(center-width2,height)],**kwds)     return polygon([(center-width2,0),
        (center+width2,0),(center+width2,height),(center-width2,height)],**kwds)
Line 650: Line 661:
def weights(n=slider(1,30,1,default=10),f=input_box(default=3*x+cos(10*x)),show_method=["Legendre", "Chebyshev", "Chebyshev2", "Trapezoid","Simpson"]): def weights(n=slider(1,30,1,default=10),f=input_box(default=3*x+cos(10*x),type=SR),
    show_method=["Legendre", "Chebyshev", "Chebyshev2", "Trapezoid","Simpson"]):
Line 659: Line 671:
    scaled_ff = fast_float(scaled_func)     scaled_ff = fast_float(scaled_func, 'x')
Line 667: Line 679:
    stems = sum(line([(x,0),(x,scaled_ff(x))],rgbcolor=(1-y,1-y,1-y),thickness=2,markersize=6,alpha=y) for x,y in coords_scaled)
    points = sum([point([(x,0),(x,scaled_ff(x))],rgbcolor='black',pointsize=30) for x,_ in coords])		     stems = sum(line([(x,0),(x,scaled_ff(x))],rgbcolor=(1-y,1-y,1-y),
        thickness=2,markersize=6,alpha=y) for x,y in coords_scaled)
    points = sum([point([(x,0),
        (x,scaled_ff(x))],rgbcolor='black',pointsize=30) for x,_ in coords])
Line 673: Line 687:
    show(graph,xmin=plot_min,xmax=plot_max)     show(graph,xmin=plot_min,xmax=plot_max,aspect_ratio="auto")
Line 681: Line 695:
    html("$$\sum_{i=1}^{i=%s}w_i\left(%s\\right)= %s\\approx %s =\int_{-1}^{1}%s \,dx$$"%(n,latex(f.subs(x="x_i")), approximation, integral, latex(scaled_func)))     html("$$\sum_{i=1}^{i=%s}w_i\left(%s\\right)= %s\\approx %s =\int_{-1}^{1}%s \,dx$$"%(n,
        latex(f), approximation, integral, latex(scaled_func)))
Line 694: Line 709:
{{{ {{{#!sagecell
Line 806: Line 821:
{{{ {{{#!sagecell
Line 843: Line 858:
velocity = derivative( position(t) )
acceleration = derivative(velocity(t))		 velocity = derivative( position(t), t)
acceleration = derivative(velocity(t), t)
Line 846: Line 861:
speed_deriv = derivative(speed) speed_deriv = derivative(speed, t)
Line 848: Line 863:
dT = derivative(tangent(t)) dT = derivative(tangent(t), t)
Line 851: Line 866:
## dB = derivative(binormal(t)) ## dB = derivative(binormal(t), t)
Line 929: Line 944:
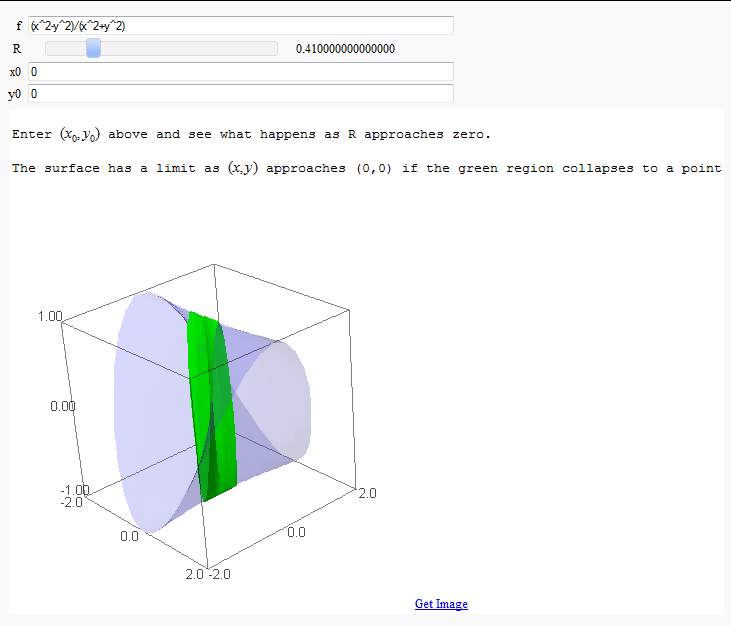
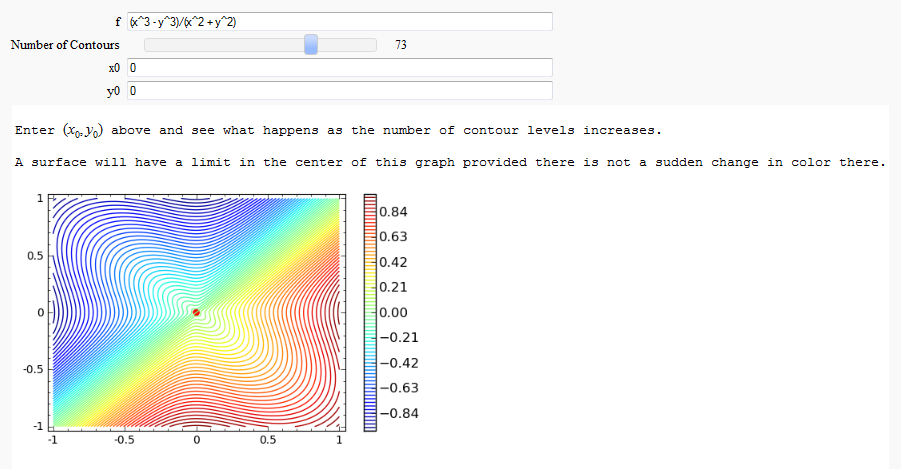
== Multivariate Limits by Definition ==
by John Travis

http://www.sagenb.org/home/pub/2828/

{{{#!sagecell
## An interactive way to demonstrate limits of multivariate functions of the form z = f(x,y)
##
## John Travis
## Mississippi College
##
## Spring 2011
##
## An updated version of this worksheet may be available at http://sagenb.mc.edu

# Starting point for radius values before collapsing in as R approaches 0.
# Functions ought to be "reasonable" within a circular domain of radius R surrounding
# the desired (x_0,y_0).

Rmax=2
@interact
def _(f=input_box(default=(x^3-y^3)/(x^2+y^2)),R=slider(0.1/10,Rmax,1/10,2),x0=(0),y0=(0)):

# converting f to cylindrical coordinates.
    g(r,t) = f(x=r*cos(t)+x0,y=r*sin(t)+y0)

# Sage graphing transformation used to see the original surface.
    cylinder = (r*cos(t)+x0,r*sin(t)+y0,z)
    surface = plot3d(g,(t,0,2*pi),(r,1/100,Rmax),transformation=cylinder,opacity=0.2)

# Regraph the surface for smaller and smaller radii controlled by the slider.
    limit = plot3d(g,(t,0,2*pi),(r,1/100,R),transformation=cylinder,rgbcolor=(0,1,0))
    
    show(surface+limit)
    print html('Enter $(x_0 ,y_0 )$ above and see what happens as R approaches zero.')
    print html('The surface has a limit as $(x,y)$ approaches ('+str(x0)+','+str(y0)+') if the green region collapses to a point')
}}}
{{attachment:3D_Limit_Defn.png}}


{{{#!sagecell
## An interactive way to demonstrate limits of multivariate functions of the form z = f(x,y)
## This one uses contour plots and so will work with functions that have asymptotic behavior.
##
## John Travis
## Mississippi College
##
## Spring 2011
##

# An increasing number of contours for z = f(x,y) are utilized surrounding a desired (x_0,y_0).
# A limit can be shown to exist at (x_0,y_0) provided the point stays trapped between adjacent
# contour lines as the number of lines increases. If the contours change wildly near the point,
# then a limit does not exist.
# Looking for two different paths to approach (x_0,y_0) that utilize a different selection of colors
# will help locate paths to use that exhibit the absence of a limit.

Rmax=2
@interact
def _(f=input_box(default=(x^3-y^3)/(x^2+y^2)),
      N=slider(5,100,1,10,label='Number of Contours'),
      x0=(0),y0=(0)):

    print html('Enter $(x_0 ,y_0 )$ above and see what happens as the number of contour levels increases.')
    print html('A surface will have a limit in the center of this graph provided there is not a sudden change in color there.')

    surface = contour_plot(f,(x,x0-1,x0+1),(y,y0-1,y0+1),cmap=True,colorbar=True,fill=False,contours=N)
    limit_point = point((x0,y0),color='red',size=30)
    show(limit_point+surface)}}}
{{attachment:3D_Limit_Defn_Contours.png}}
Line 933: Line 1021:
{{{ {{{#!sagecell
Line 986: Line 1074:
{{{
%hide
%auto		 {{{#!sagecell
Line 1047: Line 1133:
{{{ {{{#!sagecell
Line 1085: Line 1171:
{{{ {{{#!sagecell
Line 1118: Line 1204:

== Volumes over non-rectangular domains ==

by John Travis

http://www.sagenb.org/home/pub/2829/

{{{#!sagecell
## Graphing surfaces over non-rectangular domains
## John Travis
## Spring 2011
##
##
## An updated version of this worksheet may be available at http://sagenb.mc.edu
##
## Interact allows the user to input up to two inequality constraints on the
## domain when dealing with functional surfaces
##
## User inputs:
## f = "top" surface with z = f(x,y)
## g = "bottom" surface with z = g(x,y)
## condition1 = a single boundary constraint. It should not include && or | to join two conditions.
## condition2 = another boundary constraint. If there is only one constraint, just enter something true
## or even just an x (or y) in the entry blank.
##
##

var('x,y')

# f is the top surface
# g is the bottom surface
global f,g

# condition1 and condition2 are the inequality constraints. It would be nice
# to have any number of conditions connected by $$ or |
global condition1,condition2

@interact
def _(f=input_box(default=(1/3)*x^2 + (1/4)*y^2 + 5,label='$f(x)=$'),
        g=input_box(default=-1*x+0*y,label='$g(x)=$'),
        condition1=input_box(default= x^2+y^2<8,label='$Constraint_1=$'),
        condition2=input_box(default=y<sin(3*x),label='$Constraint_2=$'),
        show_3d=('Stereographic',false), show_vol=('Shade volume',true),
        dospin = ('Spin?',true),
        clr = color_selector('#faff00', label='Volume Color', widget='colorpicker', hide_box=True),
        xx = range_slider(-5, 5, 1, default=(-3,3), label='X Range'),
        yy = range_slider(-5, 5, 1, default=(-3,3), label='Y Range'),
        auto_update=false):
    
    # This is the top function actually graphed by using NaN outside domain
    def F(x,y):
        if condition1(x=x,y=y):
            if condition2(x=x,y=y):
                return f(x=x,y=y)
            else:
                return -NaN
        else:
            return -NaN

    # This is the bottom function actually graphed by using NaN outside domain
    def G(x,y):
        if condition1(x=x,y=y):
            if condition2(x=x,y=y):
                return g(x=x,y=y)
            else:
                return -NaN
        else:
            return -NaN
        
    P = Graphics()
      
# The graph of the top and bottom surfaces
    P_list = []
    P_list.append(plot3d(F,(x,xx[0],xx[1]),(y,yy[0],yy[1]),color='blue',opacity=0.9))
    P_list.append(plot3d(G,(x,xx[0],xx[1]),(y,yy[0],yy[1]),color='gray',opacity=0.9))
    
# Interpolate "layers" between the top and bottom if desired

    if show_vol:
        ratios = range(10)

        def H(x,y,r):
            return (1-r)*F(x=x,y=y)+r*G(x=x,y=y)
        P_list.extend([
        plot3d(lambda x,y: H(x,y,ratios[1]/10),(x,xx[0],xx[1]),(y,yy[0],yy[1]),opacity=0.2,color=clr),
        plot3d(lambda x,y: H(x,y,ratios[2]/10),(x,xx[0],xx[1]),(y,yy[0],yy[1]),opacity=0.2,color=clr),
        plot3d(lambda x,y: H(x,y,ratios[3]/10),(x,xx[0],xx[1]),(y,yy[0],yy[1]),opacity=0.2,color=clr),
        plot3d(lambda x,y: H(x,y,ratios[4]/10),(x,xx[0],xx[1]),(y,yy[0],yy[1]),opacity=0.2,color=clr),
        plot3d(lambda x,y: H(x,y,ratios[5]/10),(x,xx[0],xx[1]),(y,yy[0],yy[1]),opacity=0.2,color=clr),
        plot3d(lambda x,y: H(x,y,ratios[6]/10),(x,xx[0],xx[1]),(y,yy[0],yy[1]),opacity=0.2,color=clr),
        plot3d(lambda x,y: H(x,y,ratios[7]/10),(x,xx[0],xx[1]),(y,yy[0],yy[1]),opacity=0.2,color=clr),
        plot3d(lambda x,y: H(x,y,ratios[8]/10),(x,xx[0],xx[1]),(y,yy[0],yy[1]),opacity=0.2,color=clr),
        plot3d(lambda x,y: H(x,y,ratios[9]/10),(x,xx[0],xx[1]),(y,yy[0],yy[1]),opacity=0.2,color=clr)
        ])
# P = plot3d(lambda x,y: H(x,y,ratio/10),(x,xx[0],xx[1]),(y,yy[0],yy[1]),opacity=0.1)
             
           
# Now, accumulate all of the graphs into one grouped graph.
    P = sum(P_list[i] for i in range(len(P_list)))


    if show_3d:
        show(P,frame=true,axes=false,xmin=xx[0],xmax=xx[1],ymin=yy[0],ymax=yy[1],stereo='redcyan',figsize=(6,9),viewer='jmol',spin=dospin)
    else:
        show(P,frame=true,axes=false,xmin=xx[0],xmax=xx[1],ymin=yy[0],ymax=yy[1],figsize=(6,9),viewer='jmol',spin=dospin)
}}}
{{attachment:3D_Irregular_Volume.png}}

== Lateral Surface Area ==

by John Travis

http://www.sagenb.org/home/pub/2826/

{{{#!sagecell
## Display and compute the area of the lateral surface between two surfaces
## corresponding to the (scalar) line integral
## John Travis
## Spring 2011

var('x,y,t,s')
@interact
def _(f=input_box(default=6-4*x^2-y^2*2/5,label='$f(x,y) = $'),
        g=input_box(default=-2+sin(x)+sin(y),label='$g(x,y) = $'),
        u=input_box(default=cos(t),label='$u(t) = $'),
        v=input_box(default=2*sin(t),label='$v(t) = $'),
        a=input_box(default=0,label='$a = $'),
        b=input_box(default=3*pi/2,label='$b = $'),
        xx = range_slider(-5, 5, 1, default=(-1,1), label='x view'),
        yy = range_slider(-5, 5, 1, default=(-2,2), label='y view'),
        smoother=checkbox(default=false)):
        
    ds = sqrt(derivative(u(t),t)^2+derivative(v(t),t)^2)
    
# Set up the integrand to compute the line integral, making all attempts
# to simplify the result so that it looks as nice as possible.
    A = (f(x=u(t),y=v(t))-g(x=u(t),y=v(t)))*ds.simplify_trig().simplify()
    
# It is not expected that Sage can actually perform the line integral calculation.
# So, the result displayed may not be a numerical value as expected.
# Creating a good but harder example that "works" is desirable.
    line_integral = integral(A,t,a,b)
    line_integral_approx = numerical_integral(A,a,b)[0]
       
    html(r'<h4 align=center>Lateral Surface Area = $ %s $ </h4>'%latex(line_integral))

    html(r'<h4 align=center>Lateral Surface $ \approx $ %s</h2>'%str(line_integral_approx))

# Plot the top function z = f(x,y) that is being integrated.
    G = plot3d(f,(x,xx[0],xx[1]),(y,yy[0],yy[1]),opacity=0.2)
    G += plot3d(g,(x,xx[0],xx[1]),(y,yy[0],yy[1]),opacity=0.2)

# Add space curves on the surfaces "above" the domain curve (u(t),v(t))
    G += parametric_plot3d([u,v,g(x=u(t),y=v(t))],(t,a,b),thickness=2,color='red')
    G += parametric_plot3d([u,v,f(x=u(t),y=v(t))],(t,a,b),thickness=2,color='red')
    k=0
    if smoother:
        delw = 0.025
        lat_thick = 3
    else:
        delw = 0.10
        lat_thick = 10
    for w in (a,a+delw,..,b):
        G += parametric_plot3d([u(w),v(w),s*f(x=u(w),y=v(w))+(1-s)*g(x=u(w),y=v(w))],(s,0,1),thickness=lat_thick,color='yellow',opacity=0.9)
    show(G,spin=true)
}}}
{{attachment:Lateral_Surface.png}}
Line 1120: Line 1375:
{{{ {{{#!sagecell
Line 1134: Line 1389:

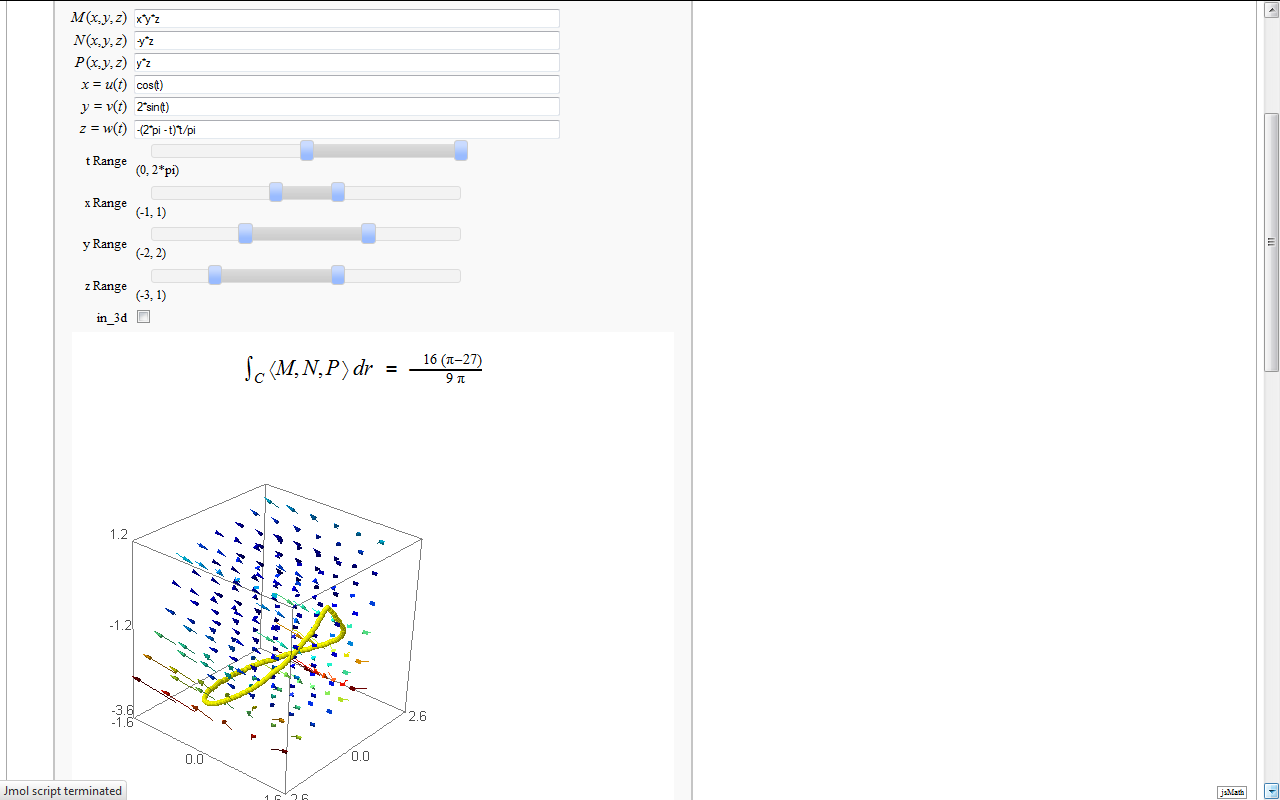
== Line Integrals in 3D Vector Field ==

by John Travis

http://www.sagenb.org/home/pub/2827/

{{{#!sagecell
## This worksheet interactively computes and displays the line integral of a 3D vector field
## over a given smooth curve C
##
## John Travis
## Mississippi College
## 06/16/11
##
## An updated version of this worksheet may be available at http://sagenb.mc.edu
##

var('x,y,z,t,s')

@interact
def _(M=input_box(default=x*y*z,label="$M(x,y,z)$"),
        N=input_box(default=-y*z,label="$N(x,y,z)$"),
        P=input_box(default=z*y,label="$P(x,y,z)$"),
        u=input_box(default=cos(t),label="$x=u(t)$"),
        v=input_box(default=2*sin(t),label="$y=v(t)$"),
        w=input_box(default=t*(t-2*pi)/pi,label="$z=w(t)$"),
        tt = range_slider(-2*pi, 2*pi, pi/6, default=(0,2*pi), label='t Range'),
        xx = range_slider(-5, 5, 1, default=(-1,1), label='x Range'),
        yy = range_slider(-5, 5, 1, default=(-2,2), label='y Range'),
        zz = range_slider(-5, 5, 1, default=(-3,1), label='z Range'),
        in_3d=checkbox(true)):

# setup the parts and then compute the line integral
    dr = [derivative(u(t),t),derivative(v(t),t),derivative(w(t),t)]
    A = (M(x=u(t),y=v(t),z=w(t))*dr[0]
        +N(x=u(t),y=v(t),z=w(t))*dr[1]
        +P(x=u(t),y=v(t),z=w(t))*dr[2])
    global line_integral
    line_integral = integral(A(t=t),t,tt[0],tt[1])
    
    html(r'<h2 align=center>$ \int_{C} \left \langle M,N,P \right \rangle dr $ = $ %s $ </h2>'%latex(line_integral))
    G = plot_vector_field3d((M,N,P),(x,xx[0],xx[1]),(y,yy[0],yy[1]),(z,zz[0],zz[1]),plot_points=6)
    G += parametric_plot3d([u,v,w],(t,tt[0],tt[1]),thickness='5',color='yellow')
    if in_3d:
        show(G,stereo='redcyan',spin=true)
    else:
        show(G,perspective_depth=true)
}}}
{{attachment:3D_Line_Integral.png}}

Sage Interactions - Calculus

goto interact main page

Contents

  1. Sage Interactions - Calculus
    1. Root Finding Using Bisection
    2. Newton's Method
    3. A contour map and 3d plot of two inverse distance functions
    4. A simple tangent line grapher
    5. Numerical integrals with the midpoint rule
    6. Numerical integrals with various rules
    7. Some polar parametric curves
    8. Function tool
    9. Newton-Raphson Root Finding
    10. Coordinate Transformations
    11. Taylor Series
    12. Illustration of the precise definition of a limit
    13. A graphical illustration of sin(x)/x -> 1 as x-> 0
    14. Quadric Surface Plotter
    15. The midpoint rule for numerically integrating a function of two variables
    16. Gaussian (Legendre) quadrature
    17. Vector Calculus, 2-D Motion
    18. Vector Calculus, 3-D Motion
    19. Multivariate Limits by Definition
    20. Directional Derivatives
    21. 3D graph with points and curves
    22. Approximating function in two variables by differential
    23. Taylor approximations in two variables
    24. Volumes over non-rectangular domains
    25. Lateral Surface Area
    26. Parametric surface example
    27. Line Integrals in 3D Vector Field

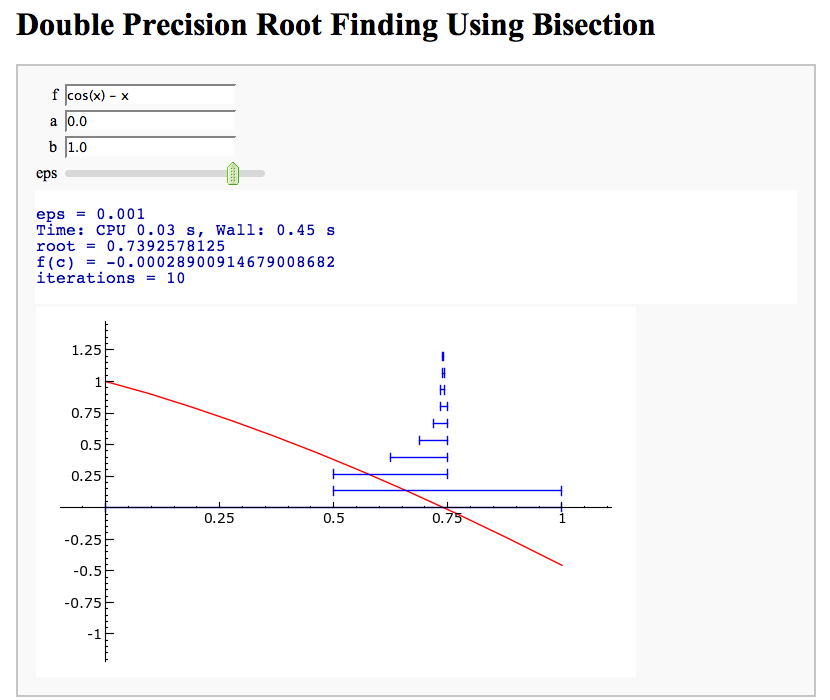
Root Finding Using Bisection

by William Stein

bisect.png

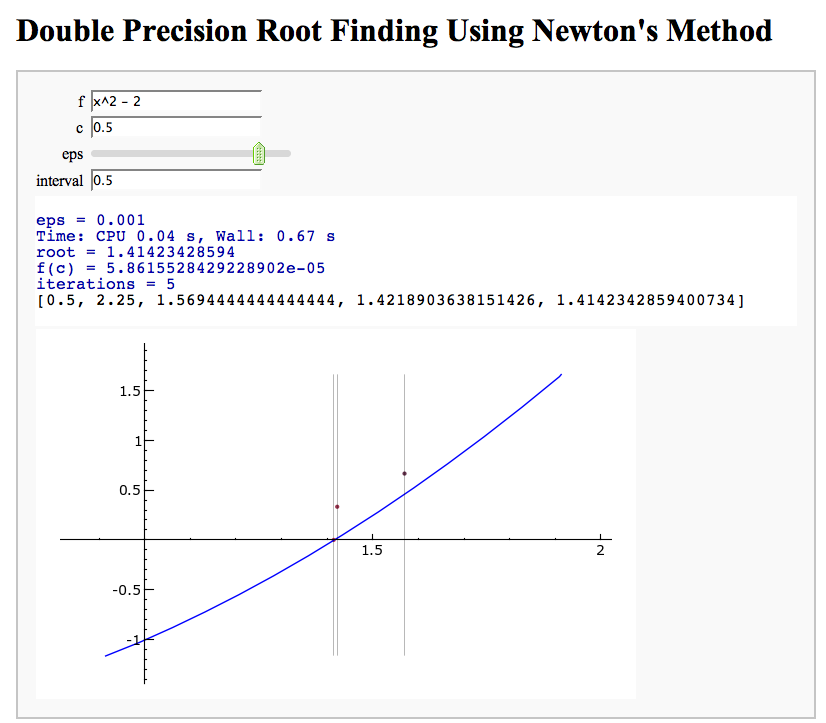
Newton's Method

Note that there is a more complicated Newton's method below.

by William Stein

http://sagenb.org/home/pub/2824/

newton.png

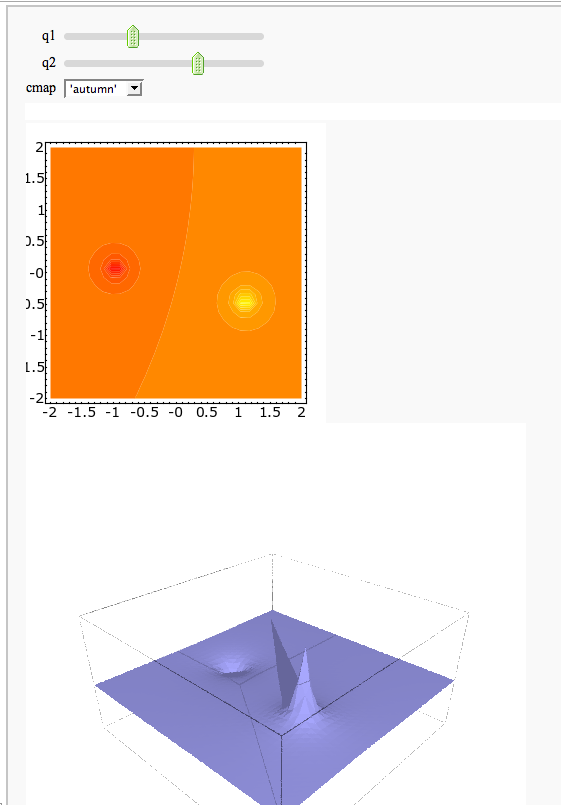
A contour map and 3d plot of two inverse distance functions

by William Stein

http://sagenb.org/home/pub/2823/

mountains.png

A simple tangent line grapher

by Marshall Hampton

tangents.png

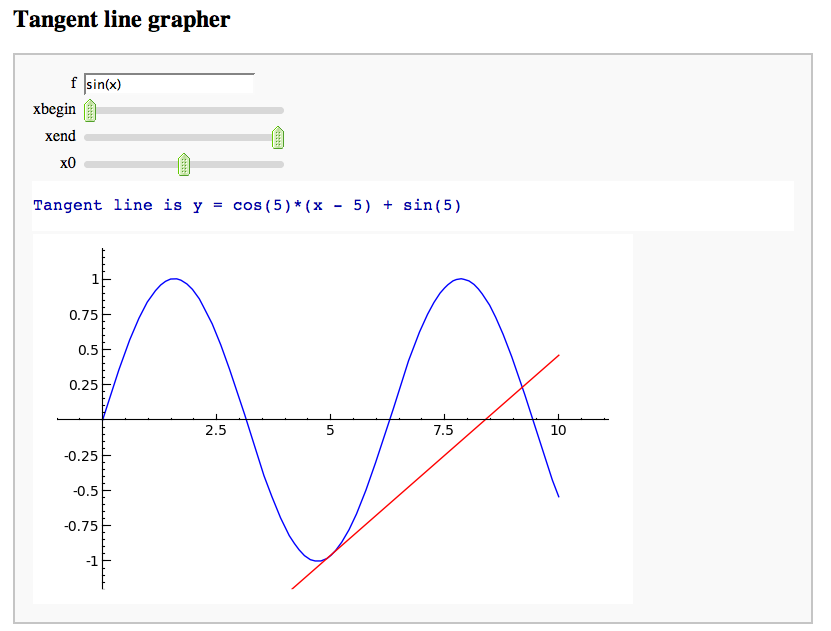
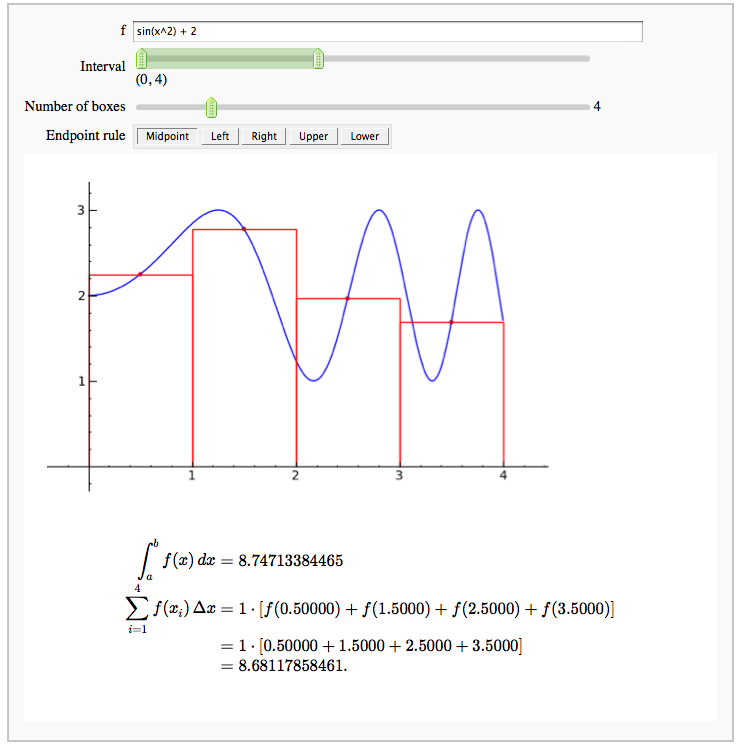
Numerical integrals with the midpoint rule

by Marshall Hampton

num_int.png

Numerical integrals with various rules

by Nick Alexander (based on the work of Marshall Hampton)

num_int2.png

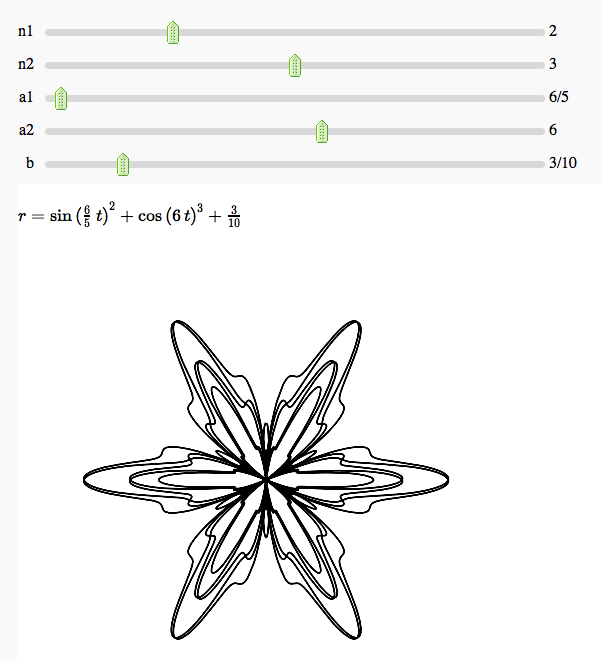
Some polar parametric curves

by Marshall Hampton. This is not very general, but could be modified to show other families of polar curves.

polarcurves1.png

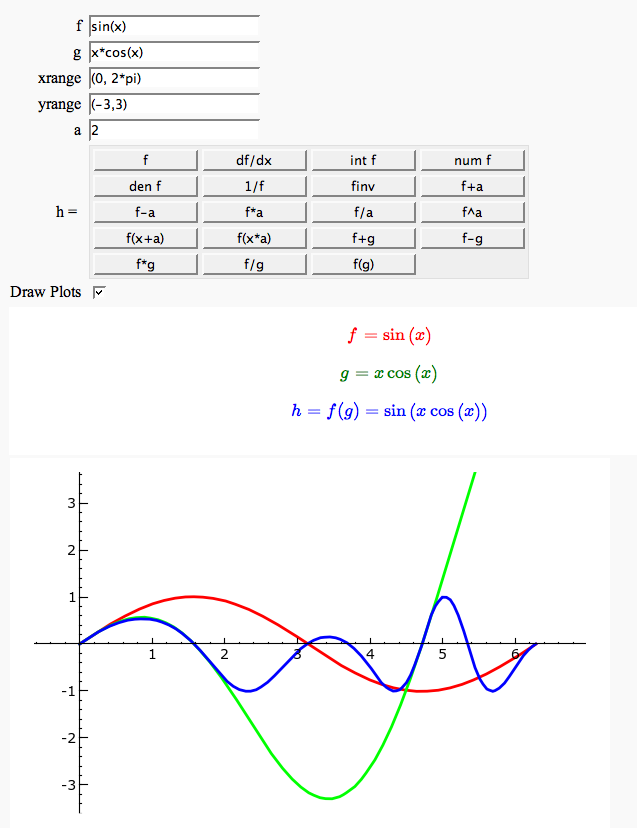
Function tool

Enter symbolic functions f, g, and a, a range, then click the appropriate button to compute and plot some combination of f, g, and a along with f and g. This is inspired by the Matlab funtool GUI.

funtool.png

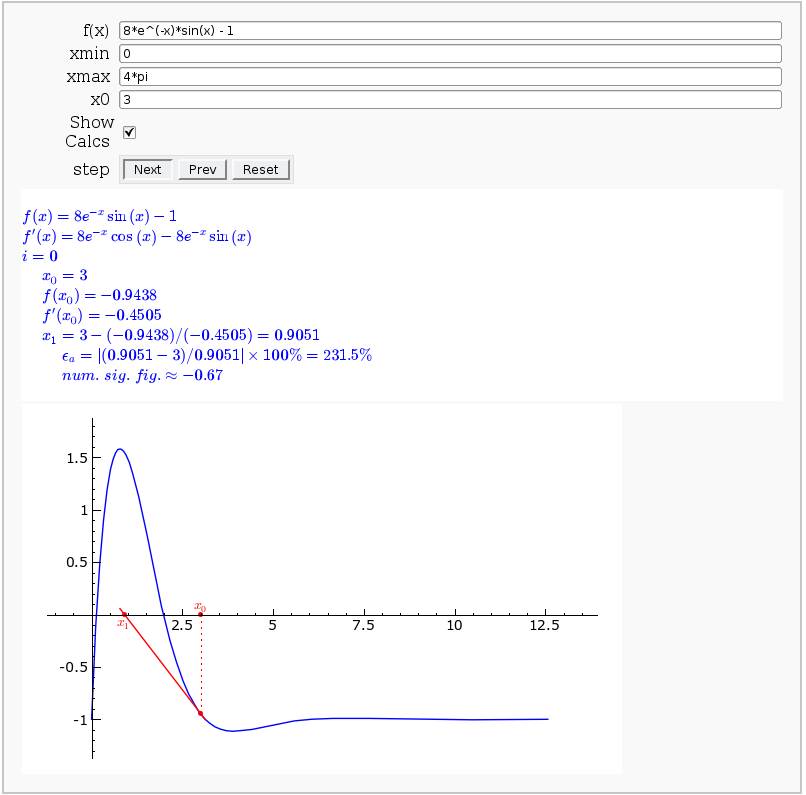
Newton-Raphson Root Finding

by Neal Holtz

This allows user to display the Newton-Raphson procedure one step at a time. It uses the heuristic that, if any of the values of the controls change, then the procedure should be re-started, else it should be continued.

newtraph.png

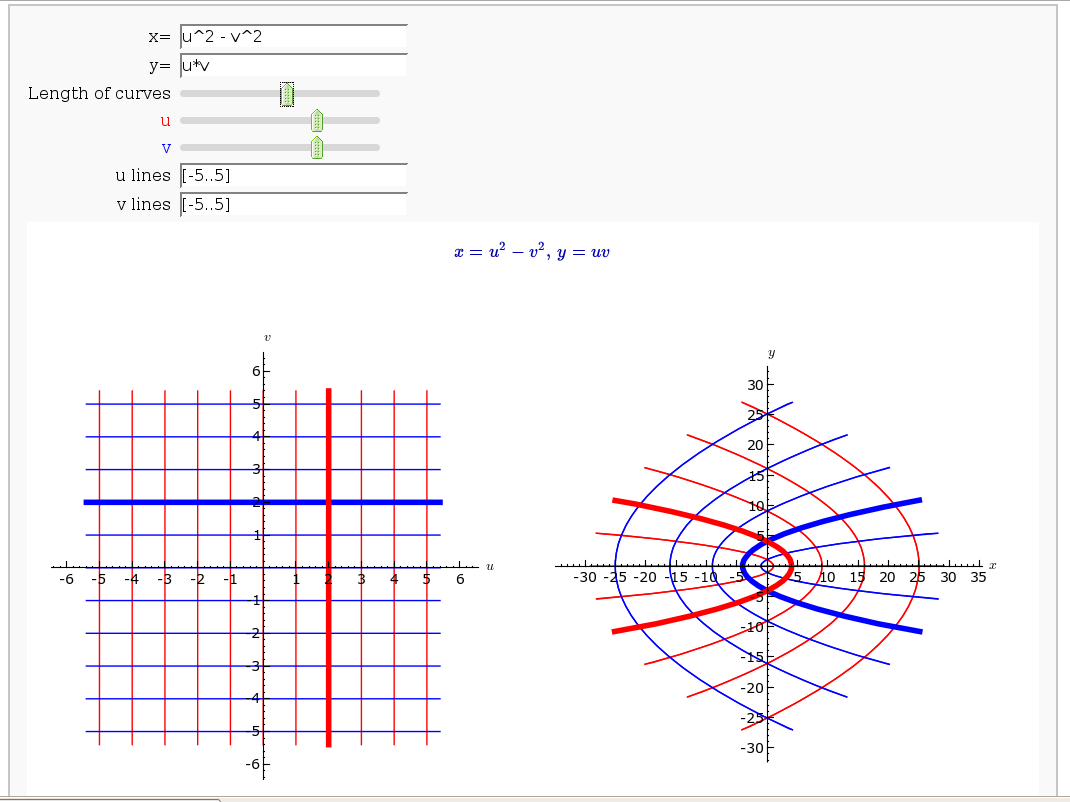
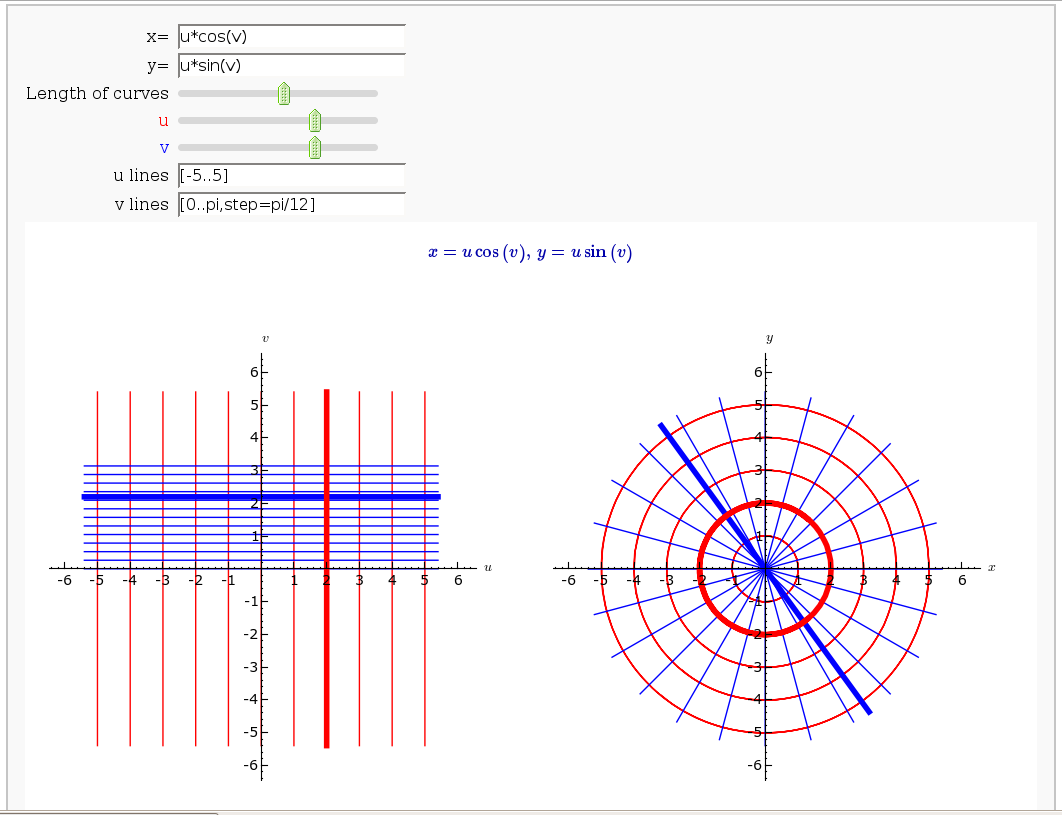
Coordinate Transformations

by Jason Grout

coordinate-transform-1.png coordinate-transform-2.png

Taylor Series

by Harald Schilly

taylor_series_animated.gif

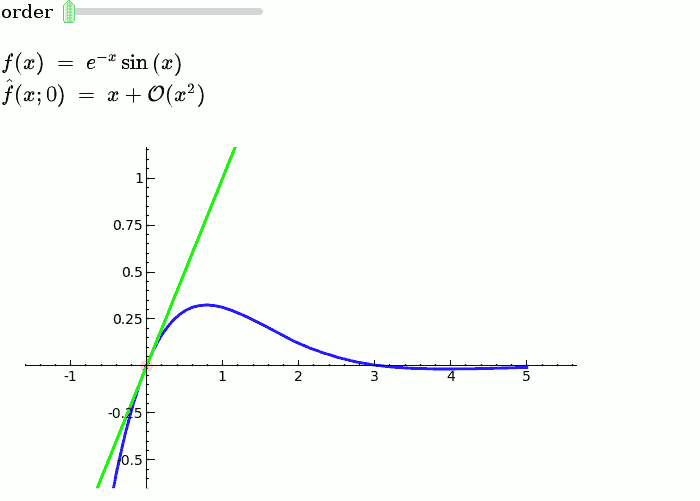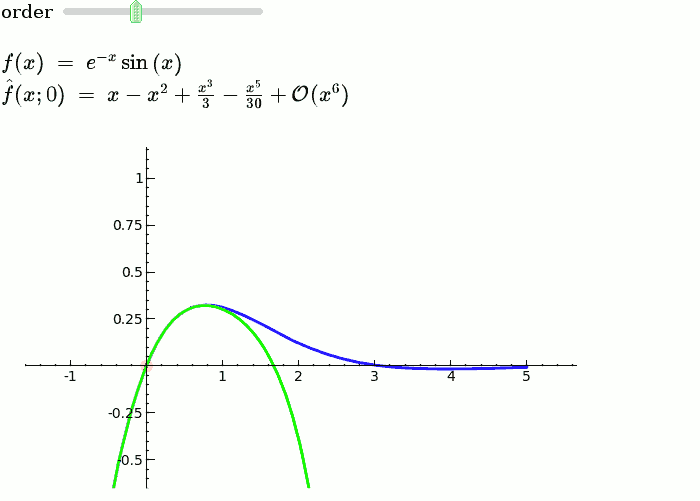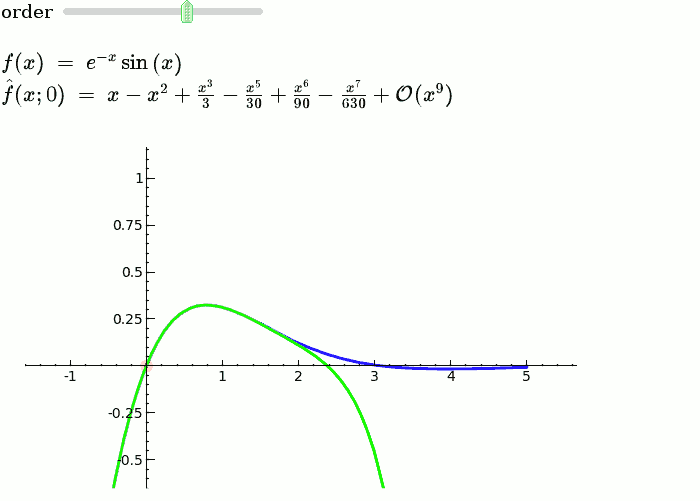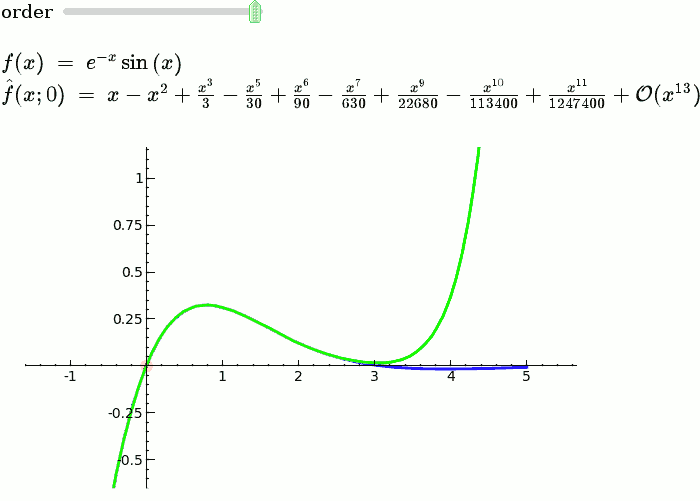
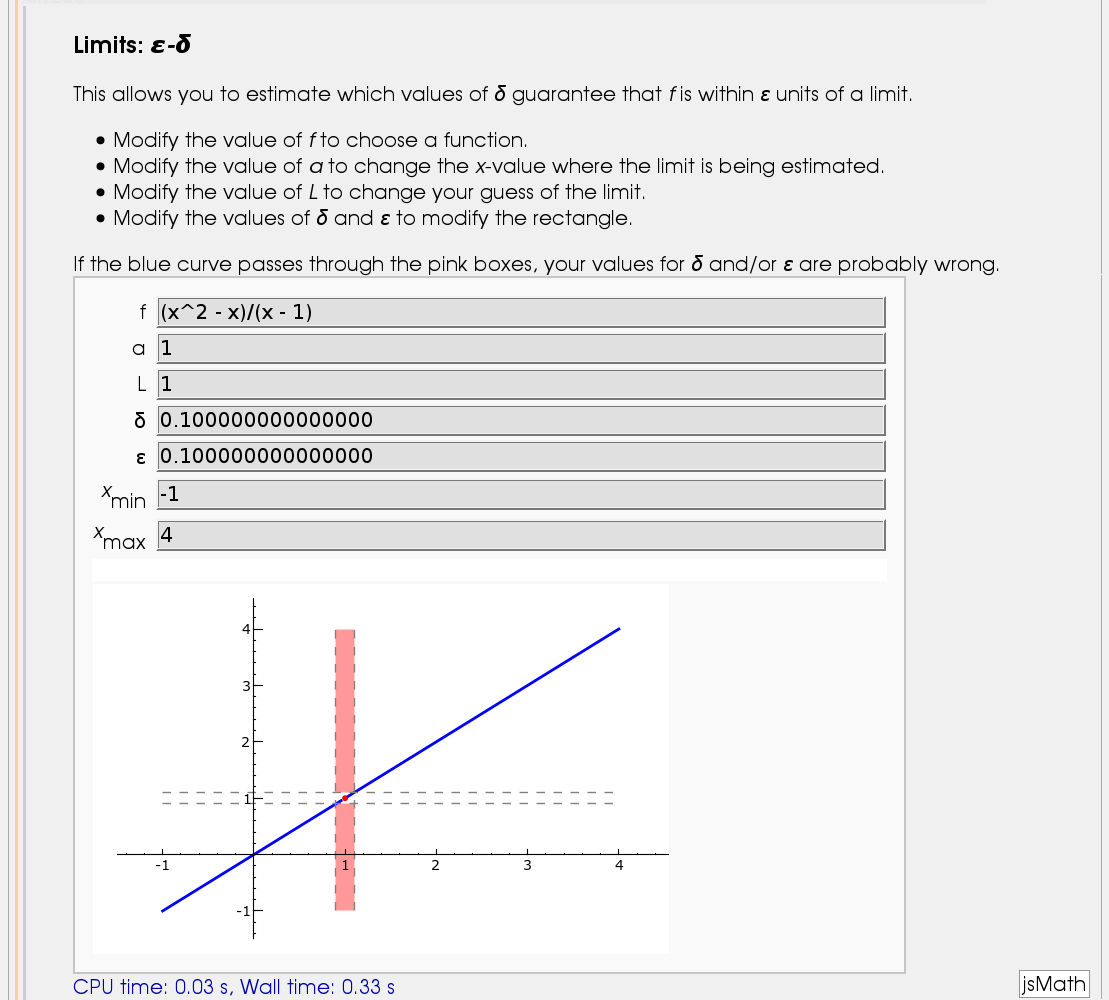
Illustration of the precise definition of a limit

by John Perry

I'll break tradition and put the image first. Apologies if this is Not A Good Thing.

snapshot_epsilon_delta.png

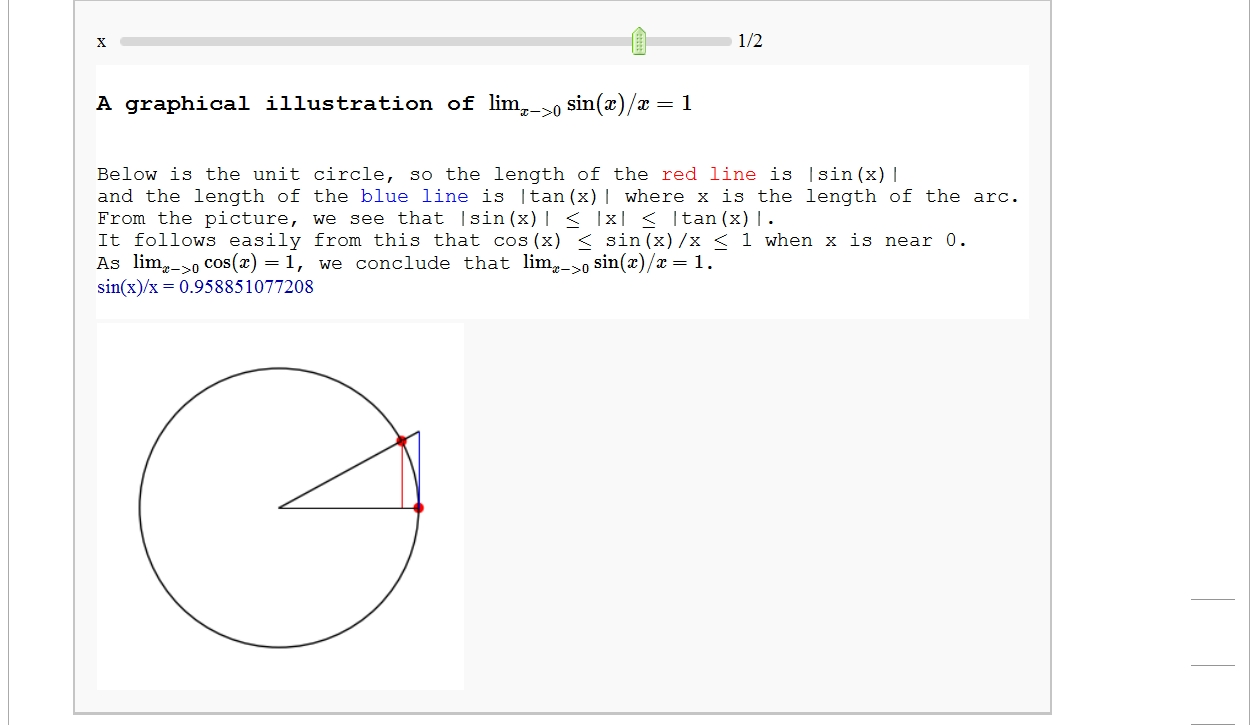
A graphical illustration of sin(x)/x -> 1 as x-> 0

by Wai Yan Pong

sinelimit.png

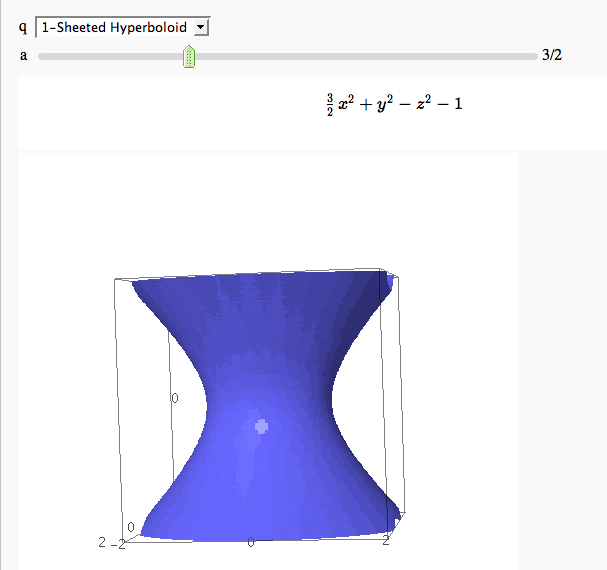
Quadric Surface Plotter

by Marshall Hampton. This is pretty simple, so I encourage people to spruce it up. In particular, it isn't set up to show all possible types of quadrics.

quadrics.png

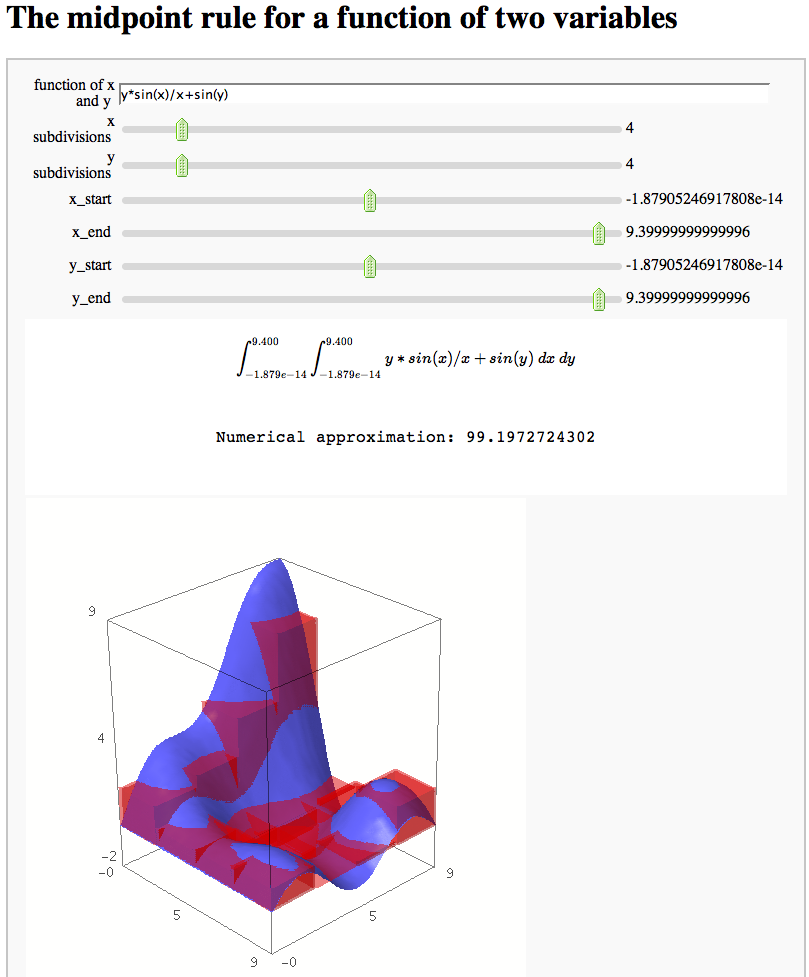
The midpoint rule for numerically integrating a function of two variables

by Marshall Hampton

numint2d.png

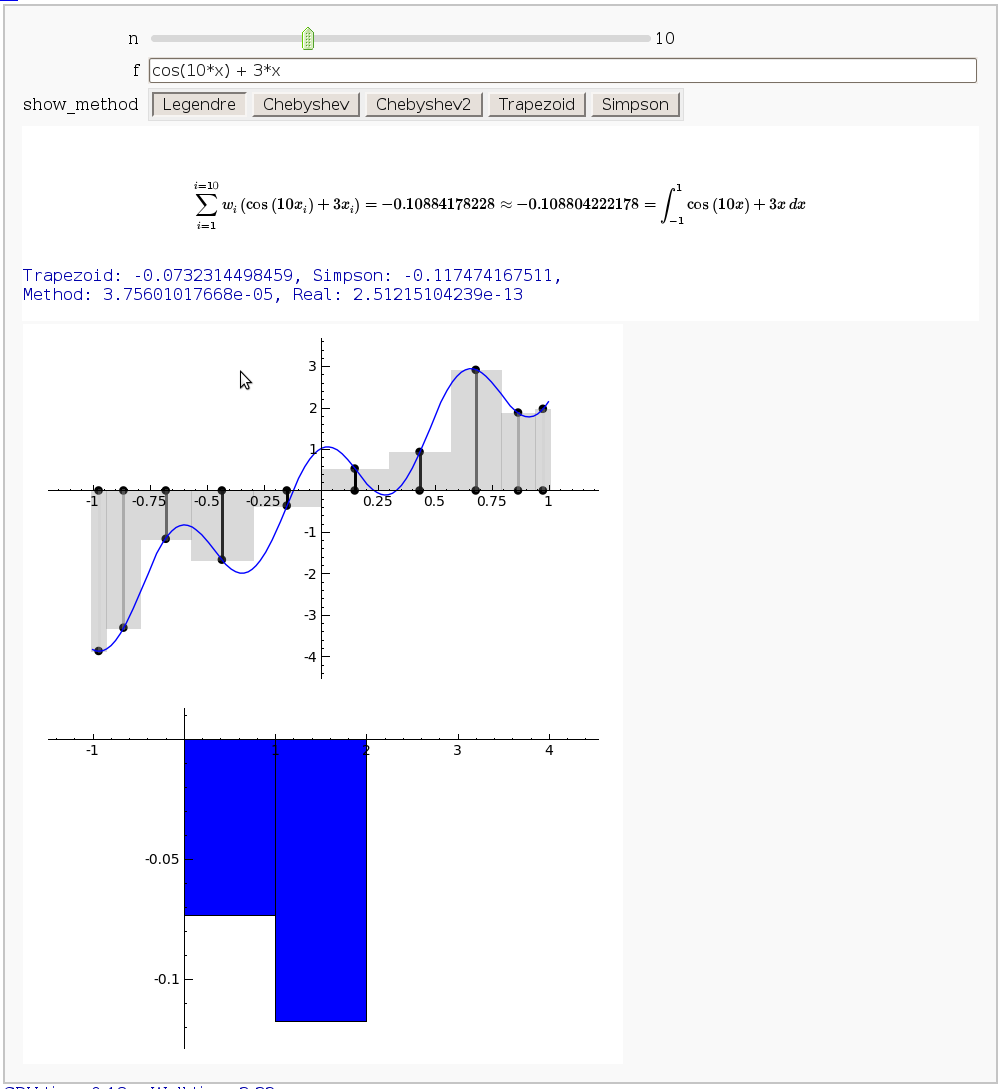
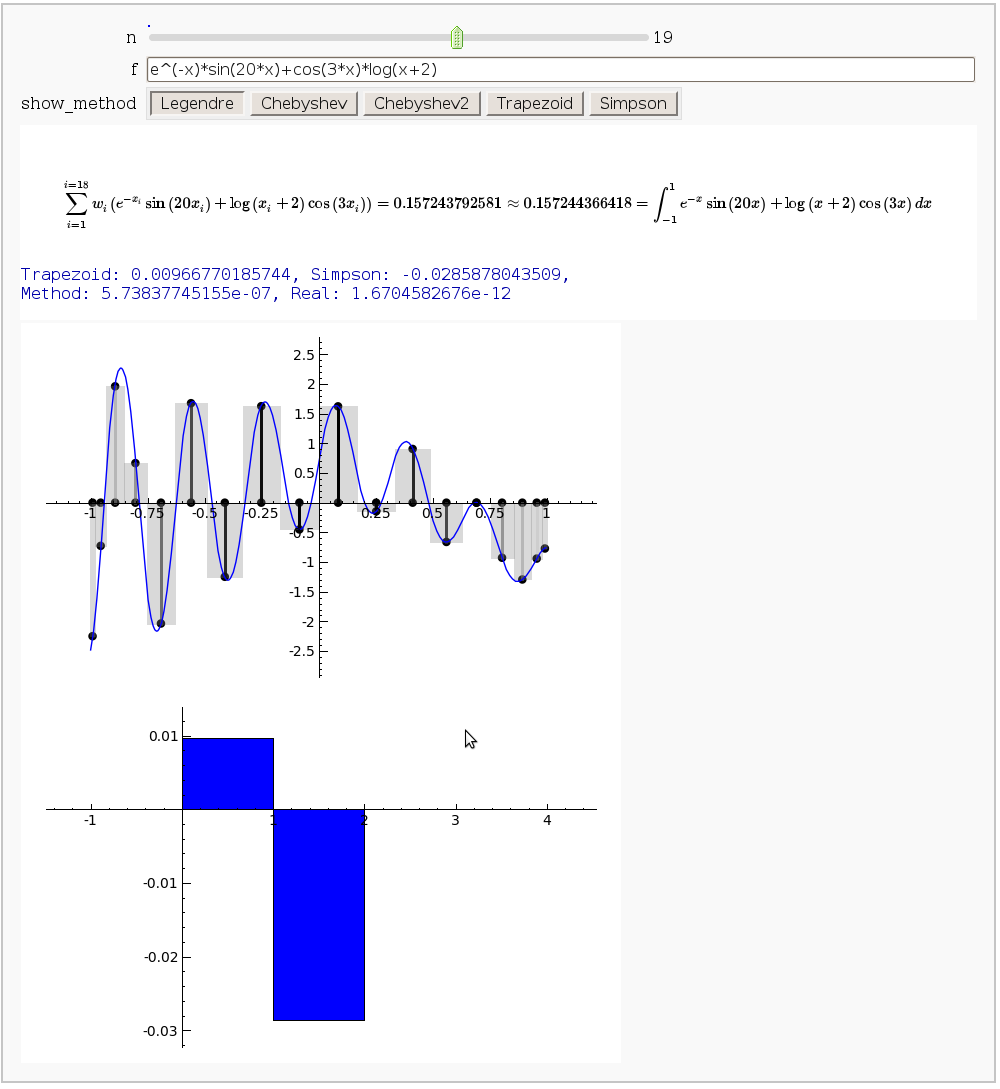
Gaussian (Legendre) quadrature

by Jason Grout

The output shows the points evaluated using Gaussian quadrature (using a weight of 1, so using Legendre polynomials). The vertical bars are shaded to represent the relative weights of the points (darker = more weight). The error in the trapezoid, Simpson, and quadrature methods is both printed out and compared through a bar graph. The "Real" error is the error returned from scipy on the definite integral.

quadrature1.png quadrature2.png

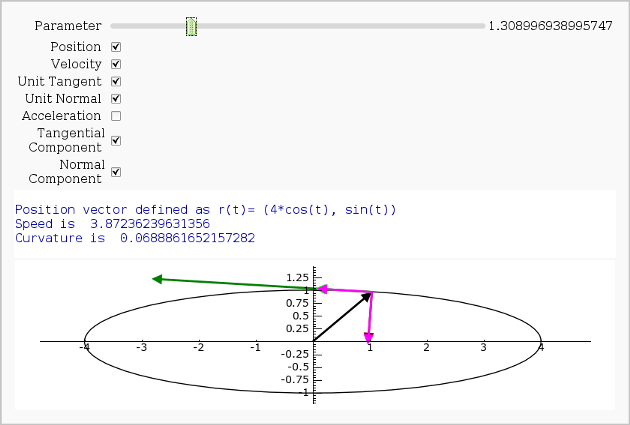
Vector Calculus, 2-D Motion

By Rob Beezer

A fast_float() version is available in a worksheet

motion2d.png

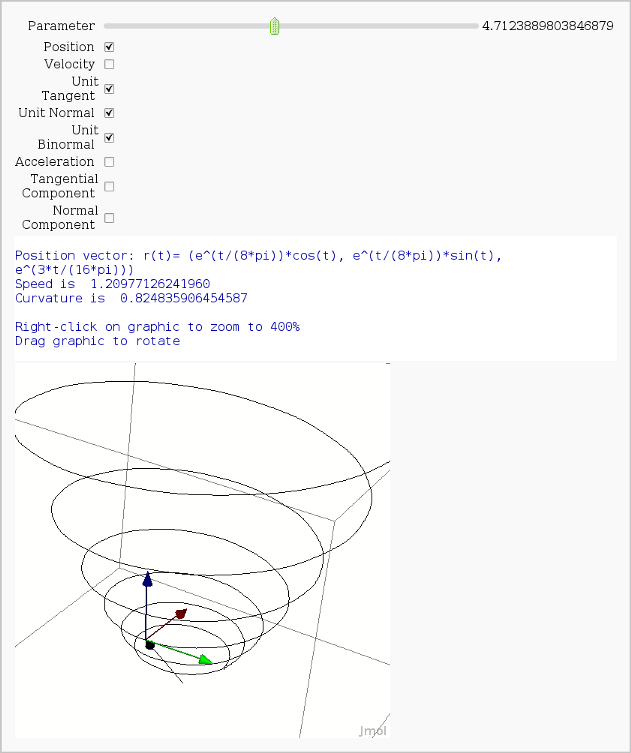
Vector Calculus, 3-D Motion

by Rob Beezer

Available as a worksheet

motion3d.png

Multivariate Limits by Definition

by John Travis

http://www.sagenb.org/home/pub/2828/

3D_Limit_Defn.png

3D_Limit_Defn_Contours.png

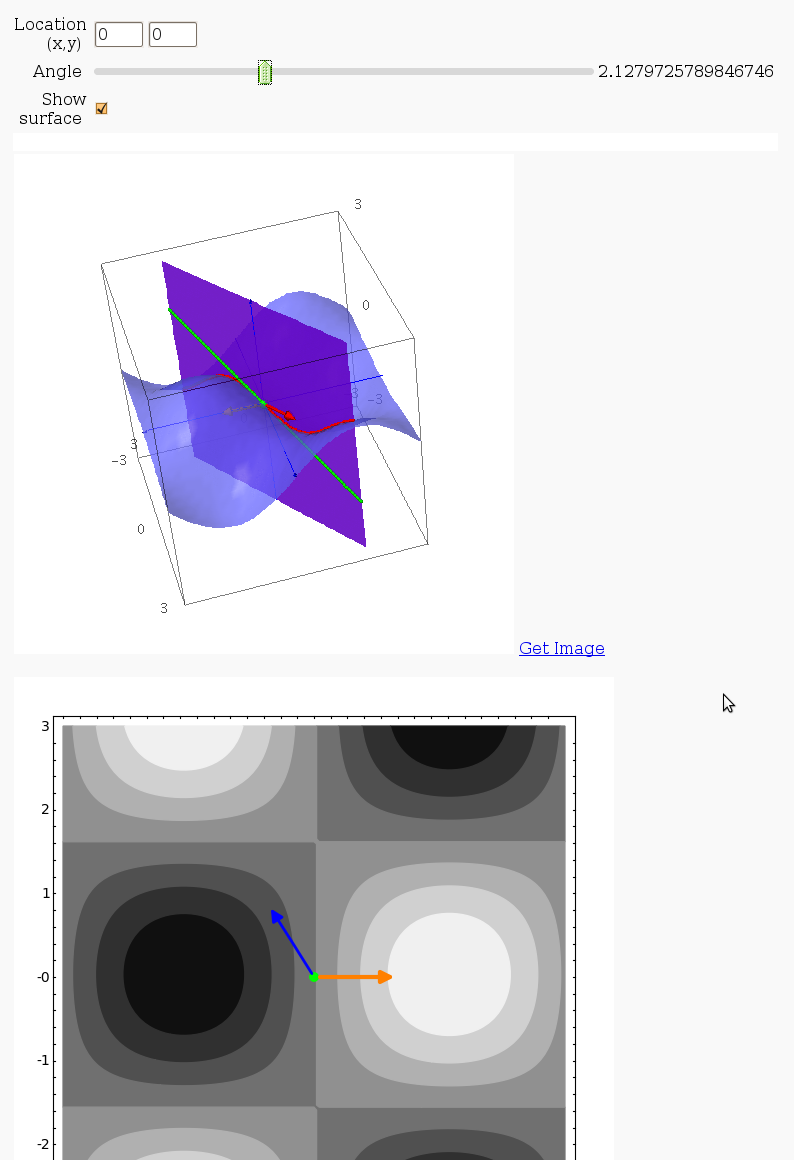
Directional Derivatives

This interact displays graphically a tangent line to a function, illustrating a directional derivative (the slope of the tangent line).

directional derivative.png

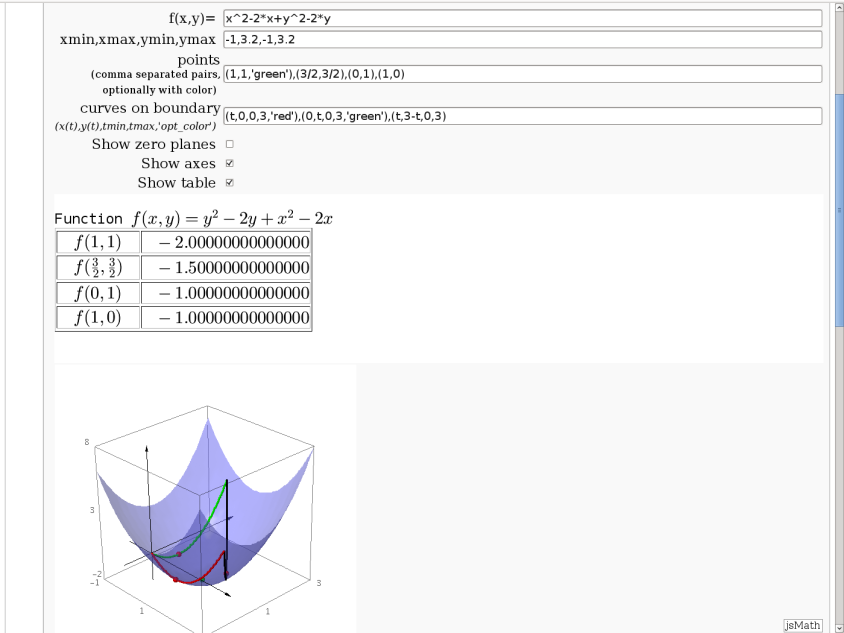
3D graph with points and curves

By Robert Marik

This sagelet is handy when showing local, constrained and absolute maxima and minima in two variables. Available as a worksheet

3Dgraph_with_points.png

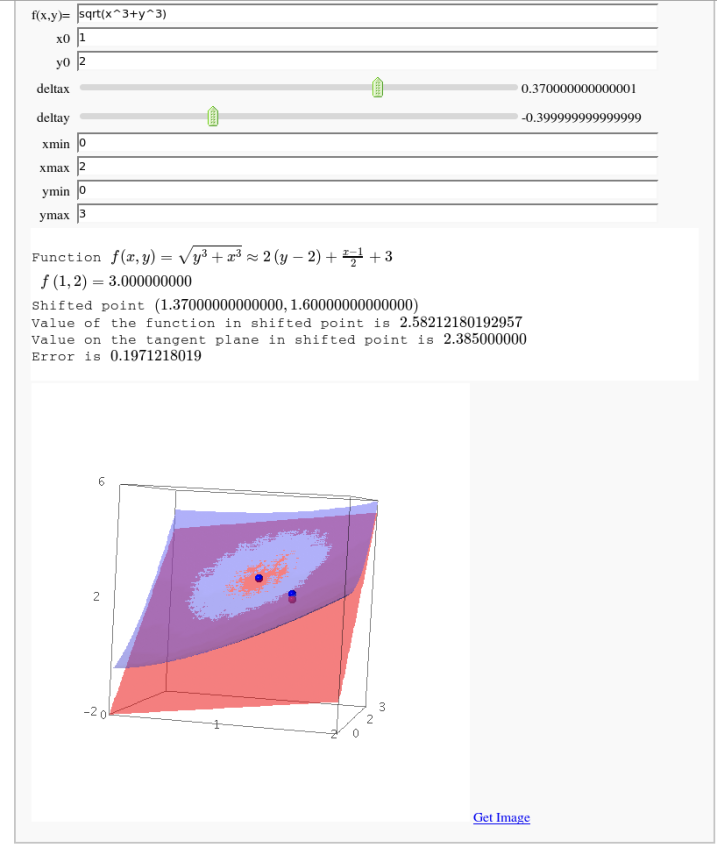
Approximating function in two variables by differential

by Robert Marik

3D_differential.png

Taylor approximations in two variables

by John Palmieri

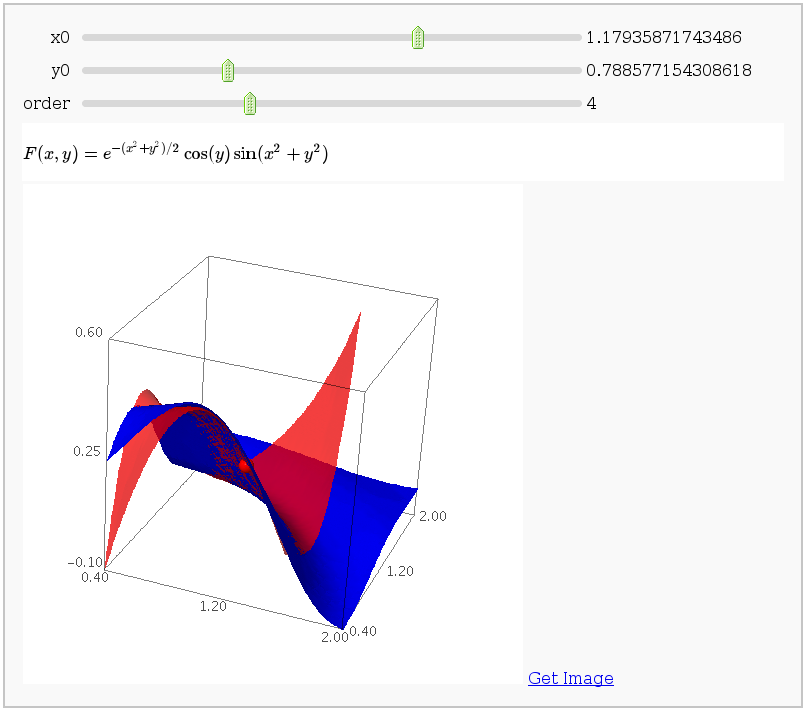
This displays the nth order Taylor approximation, for n from 1 to 10, of the function sin(x2 + y2) cos(y) exp(-(x2+y2)/2).

taylor-3d.png

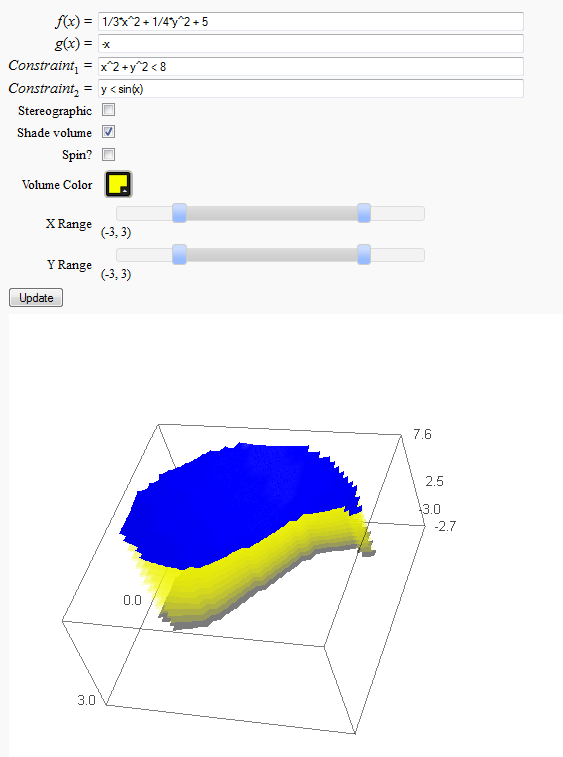
Volumes over non-rectangular domains

by John Travis

http://www.sagenb.org/home/pub/2829/

3D_Irregular_Volume.png

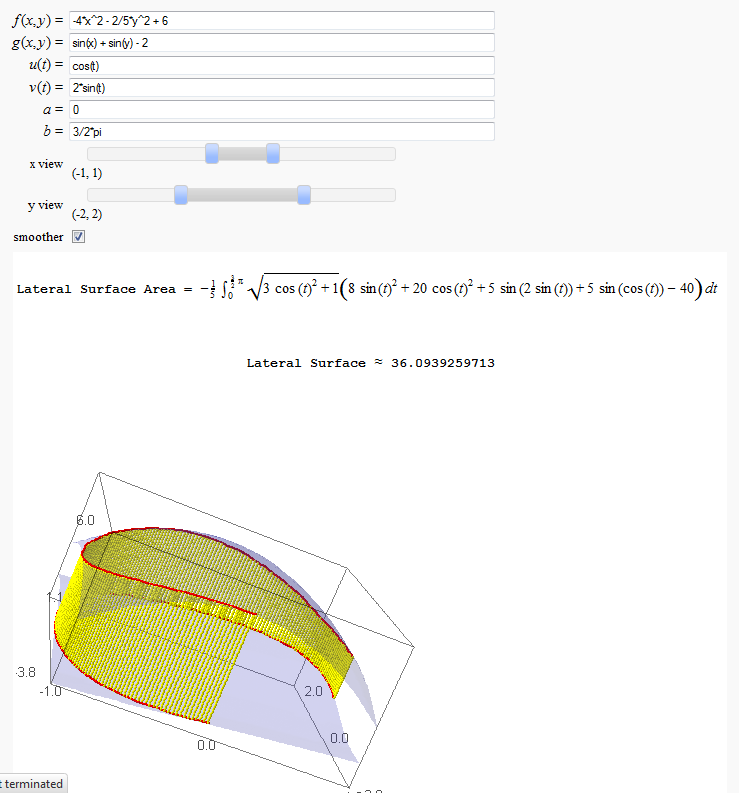
Lateral Surface Area

by John Travis

http://www.sagenb.org/home/pub/2826/

Lateral_Surface.png

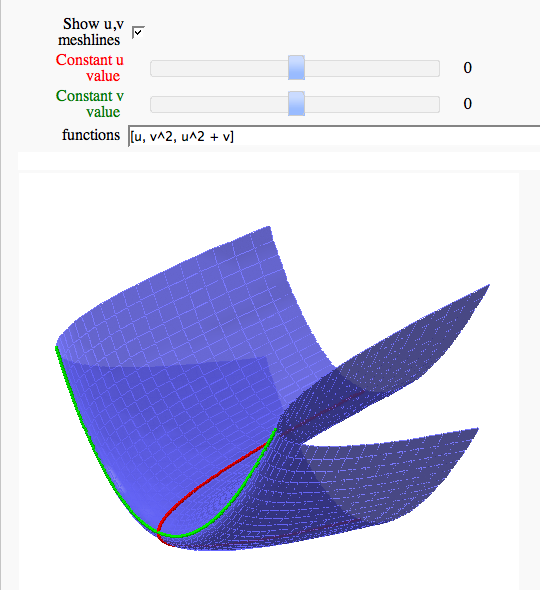
Parametric surface example

by Marshall Hampton

parametric_surface.png

Line Integrals in 3D Vector Field

by John Travis

http://www.sagenb.org/home/pub/2827/

3D_Line_Integral.png

interact/calculus (last edited 2020-08-11 14:10:09 by kcrisman)