Differences between revisions 50 and 89 (spanning 39 versions)
⇤ ← Revision 50 as of 2012-04-03 02:01:53 →
Size: 59745
Editor: bic
Comment:
← Revision 89 as of 2017-03-18 15:09:23 → ⇥
Size: 62874
Editor: mforets
Comment: fix typesetting error and a DeprecationWarning in Numerical integrals with various rules
Deletions are marked like this. Additions are marked like this.
Line 10: Line 10:
[[http://aleph.sagemath.org/?z=eJytU02P2yAQvedXjCxFC4njJP06bOOqrdqe9hBVbS-rNMIY1ki2sQDvev99B5zYzq62l5aDPcDw5jHvkQsJmbKCu2MlXKFzImNgMWQxiMbS6xngcOaxD_yQkIJMjpJZd5SlZu5IZHLPjGJZKSyht5sDDcmi46Jx8Mk5o7LWia_GaDPiNMzaMFG1E-aelRaBbwmLM3roqz5oX8qXIK_oe89nmHtuIemhUKWAH6YVIzLHNMKWGV0jxMib-dOEIZLMQpj5kIeQ0yFPSWCZJZJT2Pma12CEa00NPB6pTrMlWyDKDjYjAz98ExEbf3xYF6XP5wsk8FI-Vskm-VZcZhmGYsEvVrZ9P2OIJFStdVCwewEMrLpDqgWr7wTSBVeIgTWQuY3nlkbz0OXxDudbJaxpRJ2TsE1nhatKEu2K7YcvukVxYW8EV1bpGr5r7eCbqnNV38FP67-fg4twc7fGExGdfQy4jLtZjiZDl_jbaUs6Civo0GWDmhva372fbWnwXkpWr2Oy2r5LktWW0pMVUauOprKPe0dsN78x6Fcag0Uh6jfmNpo_scullcGpSlzoiqf-8hpOVXtfjxpMAE_1p5LoptFWOdErw1yQBLvcaEy1oOWFRtGIZQv9QJpSu5EE16U26ZUR-RU2qatUnTL_Z1161vOJZU6EjNcrjaZeHLii-X2zDDZr-g7O-8qL6HW1AaAUNRnaNcneI8bLZMe8wj_OffKInIk3gg9VTShdA9kmbxeX-JODN3jQthUpVS3ILeFxsVDYBJKH4EBBagMKF3icU299UbeVpy4meHABuHyOuCrWb2gAwcnST_4Dcj5Fzv8FOXhiD0u4eSb_HxOSmYw%3D|Interact]]
{{{		 {{{#!sagecell
Line 30: Line 29:
html("<h1>Double Precision Root Finding Using Bisection</h1>")
@interact
def _(f = cos(x) - x, a = float(0), b = float(1), eps=(-3,(-16..-1))):		 pretty_print(html("<h1>Double Precision Root Finding Using Bisection</h1>"))
@interact
def _(f = cos(x) - x, a = float(0), b = float(1), eps=(-3,(-16, -1))):
Line 36: Line 35:
         time c, intervals = bisect_method(f, a, b, eps)          c, intervals = bisect_method(f, a, b, eps)
Line 42: Line 41:
         print "f(c) = %r"%f(c)          print "f(c) = %r"%f(x=c)
Line 58: Line 57:
[[http://aleph.sagemath.org/?z=eJx1U01v2zAMvedXEAGKUKvsxCm2QxsPG7Dt1A3BgJ2yNnAcOVZrS4akJG5-_WjZzhdWATYkPvKRfJTWIgMl9k6rZSlcrteYcUg5iMpyKJNaOmHiaDJh9wOgVUMMWbhLjExWhbDIFpMnD2SVkaXw6FoYuUuc3AmsmQedeWvDm7XxTssssW6ZFTpxy97No0cev_mvn6hTUTn46pyRq60T343R5irBwzWTh5tuEicsWRdpV7g2IEEqqE2iNgK7ntmRL0vJe4PpsUaZQbKymKUMZo1O92CE2xrVyNYn6H2b2BQCIhm39ZzzdL5hUlVCrXvkHbIBiY6jesT8IXdlgcNZHn3-prc0CZgbkUortYLfWjv4IdVaqg38sc3_lx_wyMJPP-LZmOKGbPBFqiZD6gZrugVLzKjY-nlK5U65r9zLjpPwI_MXIsbgjmMQfQrDIGJk8_G7pIhPjr1u5E4E0eQZade1TAIoB8MWurHDmzbs5OCagR34-ZjeuZuXjKZpOR5yOFyYM5K0yWQoE9bxoQtSZCuEwj7LJVdrJSGtZ1Qt6PW-CpgTT1Vo11SFNT8EvRxUx22_J5XMZpXqQpt4tCq2YtRF5xQ9D9_ouiF7gJfuJBV2-CNZ7LbEShMV4p6jCqKgVUwyNlYf8nNu7JGx4pNwSt8dwT7YyoOgJ8zgFv4eH4lfhVQCF8RNVPR_YU_8vNgkfR1xl8v0VQlrY6Jl7XPh--bBCLUtvSAnYbraba73OKd8jxxq6ik-16amluMzgf4Bb3xSAg%3D%3D|Interact]]

http://sagenb.org/home/pub/2824/

{{{		 https://cloud.sagemath.com/projects/19575ea0-317e-402b-be57-368d04c113db/files/pub/2801-2901/2824-Double%20Precision%20Root%20Finding%20Using%20Newton's%20Method.sagews

{{{#!sagecell
Line 80: Line 77:
html("<h1>Double Precision Root Finding Using Newton's Method</h1>")
@interact
def _(f = x^2 - 2, c = float(0.5), eps=(-3,(-16..-1)), interval=float(0.5)):		 pretty_print(html("<h1>Double Precision Root Finding Using Newton's Method</h1>"))
@interact
def _(f = x^2 - 2, c = float(0.5), eps=(-3,(-16, -1)), interval=float(0.5)):
Line 85: Line 82:
     time z, iterates = newton_method(f, c, eps)      z, iterates = newton_method(f, c, eps)
Line 90: Line 87:
     html(iterates)      pretty_print(html(iterates))
Line 102: Line 99:
[[http://aleph.sagemath.org/?z=eJx1UsFu4yAQvfcrkHpgSLBrO4pUVUJaqb-wN29qUYITujbYgJN4v34BO-3uoVzm8QYeb2b4obSXlgv_cJQtamAsGWQlhWxHd4RQNFZhX33uH1BaoucDqzGf_NRrTBF-N1rGKIzpljgM0kZ0snyO8Wx8Cu6C7ypp4Q-ZEoPSv1O0yvURuID0KaGp7xexa3KLD8HXxDvlZwZ7Wpd5_nwg5CXJ3uiMGLpwCzhATBLZBkq-QQZO6VDi5kbIW5WBMA7GajPHHXkcyyc3Wg9w25aBQFs0BzqEsbonspjYwrwt8n28k8SF0d5M1rG6oGVePFUFzXNaHpakYMJ0xoaGuTq2baV7J7tgqhYCGlK_7A6oNRY1SOlPveXkazi1Ms3QGQ8tRXCjYSZVGA_MdxRzzWBCgxwri83aH_rl7g7oMr3kgCZv79yyn3aSSznubK7wSlGrTk79kWxPEXeDFL6x3CvDyn-OxUd3x28s8SMfvLrIpB2NhKfWZ5Ge-iYRjnVSQ2LDXaWVV7xrjnLwZ7bWQP7zclHyKi3DnovzbPQ64PhXPMK_NM4_Qg8gVAjOW7oIk78OvNxY|Interact]]

http://sagenb.org/home/pub/2823/

{{{		 https://cloud.sagemath.com/projects/19575ea0-317e-402b-be57-368d04c113db/files/pub/2801-2901/2823.sagews

{{{#!sagecell
Line 122: Line 117:
{{{
html('<h2>Tangent line grapher</h2>')		 {{{#!sagecell
pretty_print(html('<h2>Tangent line grapher</h2>'))
Line 130: Line 125:
    tanf = f(x0i) + df(x0i)*(x-x0i)     tanf = f(x=x0i) + df(x=x0i)*(x-x0i)
Line 134: Line 129:
    fmax = f.find_maximum_on_interval(prange[0], prange[1])[0]
    fmin = f.find_minimum_on_interval(prange[0], prange[1])[0]		     fmax = f.find_local_maximum(prange[0], prange[1])[0]
    fmin = f.find_local_minimum(prange[0], prange[1])[0]
Line 142: Line 137:
{{{ {{{#!sagecell
Line 151: Line 146:
    midys = [func(x_val) for x_val in midxs]     midys = [func(x=x_val) for x_val in midxs]
Line 157: Line 152:
    min_y = find_minimum_on_interval(func,a,b)[0]
    max_y = find_maximum_on_interval(func,a,b)[0]
    html('<h3>Numerical integrals with the midpoint rule</h3>')
    html('$\int_{a}^{b}{f(x) dx} {\\approx} \sum_i{f(x_i) \Delta x}$')		     min_y = min(0, find_local_minimum(func,a,b)[0])
    max_y = max(0, find_local_maximum(func,a,b)[0])
    pretty_print(html('<h3>Numerical integrals with the midpoint rule</h3>'))
    pretty_print(html('$\int_{a}^{b}{f(x) dx} {\\approx} \sum_i{f(x_i) \Delta x}$'))
Line 170: Line 165:
{{{
# by Nick Alexander (based on the work of Marshall Hampton)

var('x')		 {{{#!sagecellvar('x')
Line 181: Line 173:
    t = sage.calculus.calculus.var('t')     t = var('t')
Line 195: Line 187:
            x = find_maximum_on_interval(func, q*dx + a, q*dx + dx + a)[1]             x = find_local_maximum(func, q*dx + a, q*dx + dx + a)[1]
Line 198: Line 190:
            x = find_minimum_on_interval(func, q*dx + a, q*dx + dx + a)[1]             x = find_local_minimum(func, q*dx + a, q*dx + dx + a)[1]
Line 209: Line 201:
    min_y = min(0, find_minimum_on_interval(func,a,b)[0])
    max_y = max(0, find_maximum_on_interval(func,a,b)[0])		     min_y = min(0, find_local_minimum(func,a,b)[0])
    max_y = max(0, find_local_maximum(func,a,b)[0])
Line 226: Line 218:
    html(r'''
    <div class="math">
    \begin{align*}
   \int_{a}^{b} {f(x) \, dx} & = %s \\\
   \sum_{i=1}^{%s} {f(x_i) \, \Delta x}
      & = %s \\\
   & = %s \\\
   & = %s .
    \end{align*}
    </div>
    ''' % (numerical_answer, number_of_subdivisions, sum_html, num_html, estimated_answer))		     pretty_print(html(r'''
    <div class="math"> 
    \begin{align*}   \int_{a}^{b} {f(x) \, dx} & = %s \\\   \sum_{i=1}^{%s} {f(x_i) \, \Delta x} & = %s \\\   & = %s \\\   & = %s . \end{align*} </div>'''
                      % (numerical_answer, number_of_subdivisions, sum_html, num_html, estimated_answer)))
Line 243: Line 232:
{{{ {{{#!sagecell
Line 247: Line 236:
    html('$r=' + latex(b+sin(a1*t)^n1 + cos(a2*t)^n2)+'$')     pretty_print(html('$r=' + latex(b+sin(a1*t)^n1 + cos(a2*t)^n2)+'$'))
Line 256: Line 245:
{{{ {{{#!sagecell
Line 334: Line 323:
    html('<center><font color="red">$f = %s$</font></center>'%latex(f))
    html('<center><font color="green">$g = %s$</font></center>'%latex(g))
    html('<center><font color="blue"><b>$h = %s = %s$</b></font></center>'%(lbl, latex(h)))		     pretty_print(html('<center><font color="red">$f = %s$</font></center>'%latex(f)))
    pretty_print(html('<center><font color="green">$g = %s$</font></center>'%latex(g)))
    pretty_print(html('<center><font color="blue"><b>$h = %s = %s$</b></font></center>'%(lbl, latex(h))))
Line 354: Line 343:
{{{ {{{#!sagecell
Line 456: Line 445:
== Coordinate Transformations == == Coordinate Transformations (FIXME in Jupyter) ==
Line 460: Line 449:
{{{ {{{#!sagecell
Line 462: Line 451:
# polar coordinates
#(x,y)=(u*cos(v),u*sin(v)); (u_range,v_range)=([0..6],[0..2*pi,step=pi/12])

# weird example
(x,y)=(u^2-v^2,u*v+cos(u*v)); (u_range,v_range)=([-5..5],[-5..5])

thickness=4
square_length=.05
Line 465: Line 463:
def trans(x=input_box(u^2-v^2, label="x=",type=SR), \
         y=input_box(u*v+cos(u*v), label="y=",type=SR), \
         t_val=slider(0,10,0.2,6, label="Length of curves"), \		 def trans(x=input_box(x, label="x",type=SR),
         y=input_box(y, label="y",type=SR),
Line 470: Line 467:
         u_range=input_box(range(-5,5,1), label="u lines"),
         v_range=input_box(range(-5,5,1), label="v lines")):
     thickness=4
     u_val = min(u_range)+(max(u_range)-min(u_range))*u_percent
     v_val = min(v_range)+(max(v_range)-min(v_range))*v_percent
     t_min = -t_val
     t_max = t_val
     g1=sum([parametric_plot((i,v), (v,t_min,t_max), rgbcolor=(1,0,0)) for i in u_range])
     g2=sum([parametric_plot((u,i), (u,t_min,t_max), rgbcolor=(0,0,1)) for i in v_range])
     vline_straight=parametric_plot((u,v_val), (u,t_min,t_max), rgbcolor=(0,0,1), linestyle='-',thickness=thickness)
     uline_straight=parametric_plot((u_val, v), (v,t_min,t_max),rgbcolor=(1,0,0), linestyle='-',thickness=thickness)
 
     (g1+g2+vline_straight+uline_straight).save("uv_coord.png",aspect_ratio=1, figsize=[5,5], axes_labels=['$u$','$v$'])
     xuv = fast_float(x,'u','v')
     yuv = fast_float(y,'u','v')
     xvu = fast_float(x,'v','u')
     yvu = fast_float(y,'v','u')
     g3=sum([parametric_plot((partial(xuv,i),partial(yuv,i)), (v,t_min,t_max), rgbcolor=(1,0,0)) for i in u_range])
     g4=sum([parametric_plot((partial(xvu,i),partial(yvu,i)), (u,t_min,t_max), rgbcolor=(0,0,1)) for i in v_range])
     uline=parametric_plot((partial(xuv,u_val),partial(yuv,u_val)),(v,t_min,t_max),rgbcolor=(1,0,0), linestyle='-',thickness=thickness)
     vline=parametric_plot((partial(xvu,v_val),partial(yvu,v_val)), (u,t_min,t_max), rgbcolor=(0,0,1), linestyle='-',thickness=thickness)
     (g3+g4+vline+uline).save("xy_coord.png", aspect_ratio=1, figsize=[5,5], axes_labels=['$x$','$y$'])
     print jsmath("x=%s, \: y=%s"%(latex(x), latex(y)))
     print "<html><table><tr><td><img src='cell://uv_coord.png'/></td><td><img src='cell://xy_coord.png'/></td></tr></table></html>"		          t_val=slider(0,10,0.2,6, label="Length"),
         u_range=input_box(u_range, label="u lines"),
         v_range=input_box(v_range, label="v lines")):

    x(u,v)=x
    y(u,v)=y
    u_val = min(u_range)+(max(u_range)-min(u_range))*u_percent
    v_val = min(v_range)+(max(v_range)-min(v_range))*v_percent
    t_min = -t_val
    t_max = t_val
    uvplot=sum([parametric_plot((i,v), (v,t_min,t_max), color='red',axes_labels=['u','v'],figsize=[5,5]) for i in u_range])
    uvplot+=sum([parametric_plot((u,i), (u,t_min,t_max), color='blue',axes_labels=['u','v']) for i in v_range])
    uvplot+=parametric_plot((u,v_val), (u,t_min,t_max), rgbcolor=(0,0,1), linestyle='-',thickness=thickness)
    uvplot+=parametric_plot((u_val, v), (v,t_min,t_max),rgbcolor=(1,0,0), linestyle='-',thickness=thickness)
    pt=vector([u_val,v_val])
    du=vector([(t_max-t_min)*square_length,0])
    dv=vector([0,(t_max-t_min)*square_length])
    uvplot+=polygon([pt,pt+dv,pt+du+dv,pt+du],color='purple',alpha=0.7)
    uvplot+=line([pt,pt+dv,pt+du+dv,pt+du],color='green')

    T(u,v)=(x,y)
    xuv = fast_float(x,'u','v')
    yuv = fast_float(y,'u','v')
    xvu = fast_float(x,'v','u')
    yvu = fast_float(y,'v','u')
    xyplot=sum([parametric_plot((partial(xuv,i),partial(yuv,i)), (v,t_min,t_max), color='red', axes_labels=['x','y'],figsize=[5,5]) for i in u_range])
    xyplot+=sum([parametric_plot((partial(xvu,i),partial(yvu,i)), (u,t_min,t_max), color='blue') for i in v_range])
    xyplot+=parametric_plot((partial(xuv,u_val),partial(yuv,u_val)),(v,t_min,t_max),color='red', linestyle='-',thickness=thickness)
    xyplot+=parametric_plot((partial(xvu,v_val),partial(yvu,v_val)), (u,t_min,t_max), color='blue', linestyle='-',thickness=thickness)
    jacobian=abs(T.diff().det()).simplify_full()
    t_vals=[0..1,step=t_val*.01]
    vertices=[(x(*c),y(*c)) for c in [pt+t*dv for t in t_vals]]
    vertices+=[(x(*c),y(*c)) for c in [pt+dv+t*du for t in t_vals]]
    vertices+=[(x(*c),y(*c)) for c in [pt+(1-t)*dv+du for t in t_vals]]
    vertices+=[(x(*c),y(*c)) for c in [pt+(1-t)*du for t in t_vals]]
    xyplot+=polygon(vertices,color='purple',alpha=0.7)
    xyplot+=line(vertices,color='green')
    pretty_print(html("$T(u,v)=%s$"%(latex(T(u,v)))))
    pretty_print(html("Jacobian: $%s$"%latex(jacobian(u,v))))
    pretty_print(html("A very small region in $xy$ plane is approximately %0.4g times the size of the corresponding region in the $uv$ plane"%jacobian(u_val,v_val).n()))
    pretty_print(table([[uvplot,xyplot]]))
Line 502: Line 516:
{{{ {{{#!sagecell
Line 512: Line 526:
    html('$f(x)\;=\;%s$'%latex(f))
    html('$\hat{f}(x;%s)\;=\;%s+\mathcal{O}(x^{%s})$'%(x0,latex(ft),order+1))		     pretty_print(html('$f(x)\;=\;%s$'%latex(f)))
    pretty_print(html('$\hat{f}(x;%s)\;=\;%s+\mathcal{O}(x^{%s})$'%(x0,latex(ft),order+1)))
Line 525: Line 539:
{{{
html("<h2>Limits: <i>ε-δ</i></h2>")
html("This allows you to estimate which values of <i>δ</i> guarantee that <i>f</i> is within <i>ε</i> units of a limit.")
html("<ul><li>Modify the value of <i>f</i> to choose a function.</li>")
html("<li>Modify the value of <i>a</i> to change the <i>x</i>-value where the limit is being estimated.</li>")
html("<li>Modify the value of <i>L</i> to change your guess of the limit.</li>")
html("<li>Modify the values of <i>δ</i> and <i>ε</i> to modify the rectangle.</li></ul>")
html("If the blue curve passes through the pink boxes, your values for <i>δ</i> and/or <i>ε</i> are probably wrong.")		 {{{#!sagecell
pretty_print(html("<h2>Limits: <i>ε-δ</i></h2>"))
pretty_print(html("This allows you to estimate which values of <i>δ</i> guarantee that <i>f</i> is within <i>ε</i> units of a limit."))
pretty_print(html("<ul><li>Modify the value of <i>f</i> to choose a function.</li>"))
pretty_print(html("<li>Modify the value of <i>a</i> to change the <i>x</i>-value where the limit is being estimated.</li>"))
pretty_print(html("<li>Modify the value of <i>L</i> to change your guess of the limit.</li>"))
pretty_print(html("<li>Modify the values of <i>δ</i> and <i>ε</i> to modify the rectangle.</li></ul>"))
pretty_print(html("If the blue curve passes through the pink boxes, your values for <i>δ</i> and/or <i>ε</i> are probably wrong."))
Line 552: Line 566:
{{{ {{{#!sagecell
Line 556: Line 570:
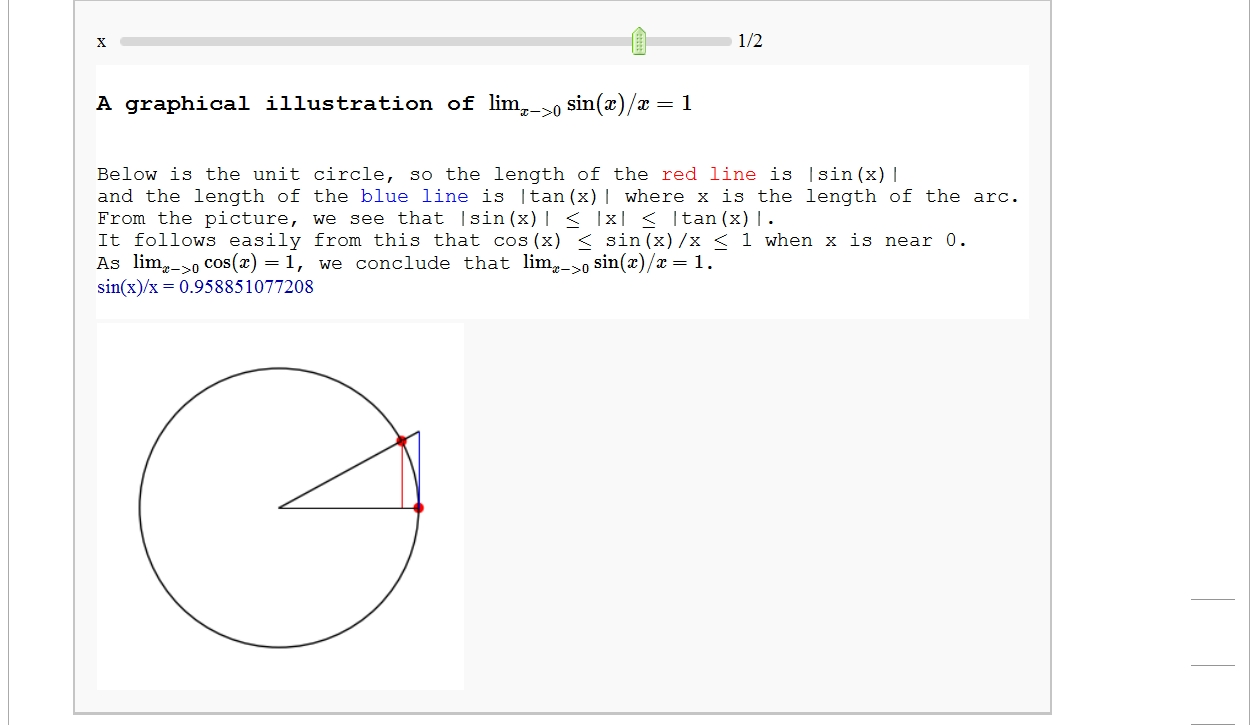
    html('<h3>A graphical illustration of $\lim_{x -> 0} \sin(x)/x =1$</h3>')
    html('Below is the unit circle, so the length of the <font color=red>red line</font> is |sin(x)|')
    html('and the length of the <font color=blue>blue line</font> is |tan(x)| where x is the length of the arc.') 
    html('From the picture, we see that |sin(x)| $\le$ |x| $\le$ |tan(x)|.')
    html('It follows easily from this that cos(x) $\le$ sin(x)/x $\le$ 1 when x is near 0.')
    html('As $\lim_{x ->0} \cos(x) =1$, we conclude that $\lim_{x -> 0} \sin(x)/x =1$.')		     pretty_print(html('<h3>A graphical illustration of $\lim_{x -> 0} \sin(x)/x =1$</h3>'))
    pretty_print(html('Below is the unit circle, so the length of the <font color=red>red line</font> is |sin(x)|'))
    pretty_print(html('and the length of the <font color=blue>blue line</font> is |tan(x)| where x is the length of the arc.'))
    pretty_print(html('From the picture, we see that |sin(x)| $\le$ |x| $\le$ |tan(x)|.'))
    pretty_print(html('It follows easily from this that cos(x) $\le$ sin(x)/x $\le$ 1 when x is near 0.'))
    pretty_print(html('As $\lim_{x ->0} \cos(x) =1$, we conclude that $\lim_{x -> 0} \sin(x)/x =1$.'))
Line 578: Line 592:
{{{ {{{#!sagecell
Line 593: Line 607:
{{{ {{{#!sagecell
Line 612: Line 626:
sin,cos = math.sin,math.cos
html("<h1>The midpoint rule for a function of two variables</h1>")
pretty_print(html("<h1>The midpoint rule for a function of two variables</h1>"))
Line 628: Line 642:
    html("$$\int_{"+str(R16(y_start))+"}^{"+str(R16(y_end))+"} "+ "\int_{"+str(R16(x_start))+"}^{"+str(R16(x_end))+"} "+func+"\ dx \ dy$$")
    html('<p style="text-align: center;">Numerical approximation: ' + str(num_approx)+'</p>')		     pretty_print(html("$$\int_{"+str(R16(y_start))+"}^{"+str(R16(y_end))+"} "+ "\int_{"+str(R16(x_start))+"}^{"+str(R16(x_end))+"} "+func+"\ dx \ dy$$"))
    pretty_print(html('<p style="text-align: center;">Numerical approximation: ' + str(num_approx)+'</p>'))
Line 639: Line 653:
{{{ {{{#!sagecell
Line 700: Line 714:
    html("$$\sum_{i=1}^{i=%s}w_i\left(%s\\right)= %s\\approx %s =\int_{-1}^{1}%s \,dx$$"%(n,
        latex(f), approximation, integral, latex(scaled_func)))		     pretty_print(html("$$\sum_{i=1}^{i=%s}w_i\left(%s\\right)= %s\\approx %s =\int_{-1}^{1}%s \,dx$$"%(n,
        latex(f), approximation, integral, latex(scaled_func))))
Line 714: Line 728:
{{{ {{{#!sagecell
Line 745: Line 759:
velocity = derivative( position(t) )
acceleration = derivative(velocity(t))		 velocity = derivative(position(t), t)
acceleration = derivative(velocity(t), t)
Line 748: Line 762:
speed_deriv = derivative(speed) speed_deriv = derivative(speed, t)
Line 750: Line 764:
dT = derivative(tangent(t)) dT = derivative(tangent(t), t)
Line 821: Line 835:
== Vector Calculus, 3-D Motion == == Vector Calculus, 3-D Motion (FIXME) ==
Line 826: Line 840:
{{{ {{{#!sagecell
Line 863: Line 877:
velocity = derivative( position(t) )
acceleration = derivative(velocity(t))		 velocity = derivative( position(t), t)
acceleration = derivative(velocity(t), t)
Line 866: Line 880:
speed_deriv = derivative(speed) speed_deriv = derivative(speed, t)
Line 868: Line 882:
dT = derivative(tangent(t)) dT = derivative(tangent(t), t)
Line 871: Line 885:
## dB = derivative(binormal(t)) ## dB = derivative(binormal(t), t)
Line 952: Line 966:
http://www.sagenb.org/home/pub/2828/

{{{		 http://sagenb.mc.edu/home/pub/97/

{{{#!sagecell
Line 962: Line 976:
## An updated version of this worksheet may be available at http://sagenb.mc.edu
Line 967: Line 980:
var('x,y,z')
Rmin=1/10
Line 969: Line 983:
@interact
def _(f=input_box(default=(x^3-y^3)/(x^2+y^2)),R=slider(0.1/10,Rmax,1/10,2),x0=(0),y0=(0)):		 @interact(layout=dict(top=[['f'],['x0'],['y0']],
bottom=[['in_3d','curves','R','graphjmol']]))
def _(f=input_box((x^2-y^2)/(x^2+y^2),width=30,label='$f(x)$'),
        R=slider(Rmin,Rmax,1/10,Rmax,label=',   $R$'),
        x0=input_box(0,width=10,label='$x_0$'),
        y0=input_box(0,width=10,label='$y_0$'),
        curves=checkbox(default=false,label='Show curves'),
        in_3d=checkbox(default=false,label='3D'),
        graphjmol=checkbox(default=true,label='Interactive graph')):
    if graphjmol:
        view_method = 'jmol'
    else:
        view_method = 'tachyon'
Line 978: Line 1003:
    
Line 980: Line 1005:
    limit = plot3d(g,(t,0,2*pi),(r,1/100,R),transformation=cylinder,rgbcolor=(0,1,0))     collapsing_surface = plot3d(g,(t,0,2*pi),(r,1/100,R),transformation=cylinder,rgbcolor=(0,1,0))
Line 982: Line 1007:
    show(surface+limit)
    print html('Enter $(x_0 ,y_0 )$ above and see what happens as R approaches zero.')
    print html('The surface has a limit as $(x,y)$ approaches ('+str(x0)+','+str(y0)+') if the green region collapses to a point')		     G = surface+collapsing_surface
    pretty_print(html('Enter $(x_0 ,y_0 )$ above and see what happens as $ R \\rightarrow 0 $.'))
    pretty_print(html('The surface has a limit as $(x,y) \\rightarrow $ ('+str(x0)+','+str(y0)+') if the green region collapses to a point.'))

# If checked, add a couple of curves on the surface corresponding to limit as x->x0 for y=x^(3/5),
# and as y->y0 for x=y^(3/5). Should make this more robust but perhaps using
# these relatively obtuse curves could eliminate problems.

    if curves:
        curve_x = parametric_plot3d([x0-t,y0-t^(3/5),f(x=x0-t,y=y0-t^(3/5))],(t,Rmin,Rmax),color='red',thickness=10)
        curve_y = parametric_plot3d([x0+t^(3/5),y0+t,f(x=x0+t^(3/5),y=y0+t)],(t,Rmin,Rmax),color='red',thickness=10)
        R2 = Rmin/4
        G += arrow((x0-Rmin,y0-Rmin^(3/5),f(x=x0-Rmin,y=y0-Rmin^(3/5))),(x0-R2,y0-R2^(3/5),f(x=x0-R2,y=y0-R2^(3/5))),size=30 )
        G += arrow((x0+Rmin^(3/5),y0+Rmin,f(x=x0+Rmin^(3/5),y=y0+Rmin)),(x0+R2^(3/5),y0+R2,f(x=x0+R2^(3/5),y=y0+R2)),size=30 )

        limit_x = limit(f(x=x0-t,y=y0-t^(3/5)),t=0)
        limit_y = limit(f(x=x0+t^(3/5),y=y0+t),t=0)
        text_x = text3d(limit_x,(x0,y0,limit_x))
        text_y = text3d(limit_y,(x0,y0,limit_y))
        G += curve_x+curve_y+text_x+text_y
 
    
        pretty_print(html('The red curves represent a couple of trajectories on the surface. If they do not meet, then'))
        pretty_print(html('there is also no limit. (If computer hangs up, likely the computer can not do these limits.)'))
        pretty_print(html('\n<center><font color="red">$\lim_{(x,?)\\rightarrow(x_0,y_0)} f(x,y) =%s$</font>'%str(limit_x)+' and <font color="red">$\lim_{(?,y)\\rightarrow(x_0,y_0)} f(x,y) =%s$</font></center>'%str(limit_y)))
        
    if in_3d:
        show(G,stereo="redcyan",viewer=view_method)
    else:
        show(G,perspective_depth=true,viewer=view_method)
Line 989: Line 1041:
{{{ {{{#!sagecell
Line 1006: Line 1059:
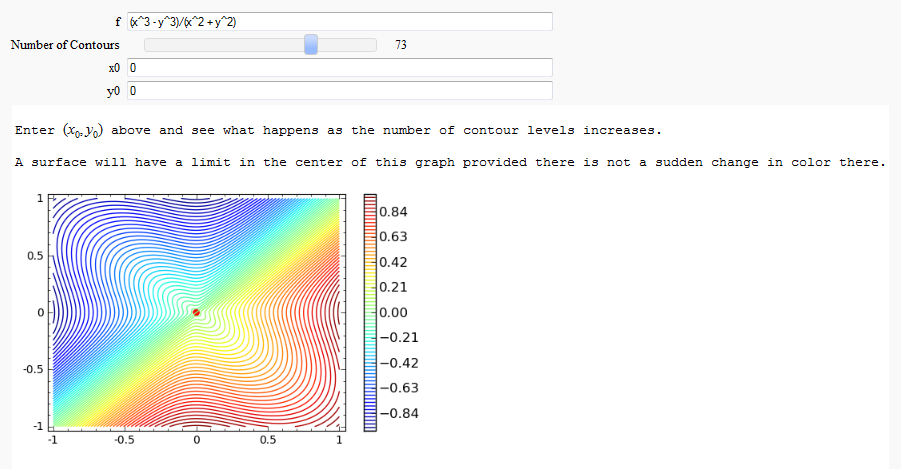
Rmax=2
@interact
def _(f=input_box(default=(x^3-y^3)/(x^2+y^2)),
      N=slider(5,100,1,10,label='Number of Contours'),
      x0=(0),y0=(0)):

    print html('Enter $(x_0 ,y_0 )$ above and see what happens as the number of contour levels increases.')
    print html('A surface will have a limit in the center of this graph provided there is not a sudden change in color there.') 		var('x,y,z,u')
@interact(layout=dict(top=[['f'],['x0'],['y0']],
bottom=[['N'],['R']]))
def _(f=input_box(default=(x*y^2)/(x^2+y^4),width=30,label='$f(x)$'),
        N=slider(5,100,1,10,label='Number of Contours'),
        R=slider(0.1,1,0.01,1,label='Radius of circular neighborhood'),
        x0=input_box(0,width=10,label='$x_0$'),
        y0=input_box(0,width=10,label='$y_0$')):

    pretty_print(html('Enter $(x_0 ,y_0 )$ above and see what happens as the number of contour levels $\\rightarrow \infty $.'))
    pretty_print(html('A surface will have a limit in the center of this graph provided there is not a sudden change in color there.'))

# Need to make certain the min and max contour lines are not huge due to asymptotes. If so, clip and start contours at some reasonable
# values so that there are a nice collection of contours to show around the desired point.
Line 1016: Line 1075:
    surface += parametric_plot([R*cos(u),R*sin(u)],[0,2*pi],color='black')
# Nice to use if f=x*y^2/(x^2 + y^4)
# var('u')
# surface += parametric_plot([u^2,u],[u,-1,1],color='black')
Line 1017: Line 1080:
    show(limit_point+surface)}}} # show(limit_point+surface)
    pretty_print(table([[surface],['hi']]))
}}}
Line 1026: Line 1091:
{{{ {{{#!sagecell
Line 1079: Line 1144:
{{{
%hide
%auto		 {{{#!sagecell
Line 1096: Line 1159:
 html(r'Function $ f(x,y)=%s$ '%latex(f(x,y)))  pretty_print(html(r'Function $ f(x,y)=%s$ '%latex(f(x,y))))
Line 1110: Line 1173:
              html(r'<tr><td>$\quad f(%s,%s)\quad $</td><td>$\quad %s$</td>\
              </tr>'%(latex(x0),latex(y0),z0.n()))		               pretty_print(html(r'<tr><td>$\quad f(%s,%s)\quad $</td><td>$\quad %s$</td>\
              </tr>'%(latex(x0),latex(y0),z0.n())))
Line 1140: Line 1203:
{{{ {{{#!sagecell
Line 1144: Line 1207:
html('Points x0 and y0 are values where the exact value of the function \ pretty_print(html('Points x0 and y0 are values where the exact value of the function \
Line 1146: Line 1209:
and approximation by differential at shifted point are compared.') and approximation by differential at shifted point are compared.'))
Line 1164: Line 1227:
  html(r'Function $ f(x,y)=%s \approx %s $ '%(latex(f(x,y)),latex(tangent(x,y))))
  html(r' $f %s = %s$'%(latex((x0,y0)),latex(exact_value_ori)))
  html(r'Shifted point $%s$'%latex(((x0+deltax),(y0+deltay))))
  html(r'Value of the function in shifted point is $%s$'%f(x0+deltax,y0+deltay))
  html(r'Value on the tangent plane in shifted point is $%s$'%latex(approx_value))
  html(r'Error is $%s$'%latex(abs_error)) 		   pretty_print(html(r'Function $ f(x,y)=%s \approx %s $ '%(latex(f(x,y)),latex(tangent(x,y)))))
  pretty_print(html(r' $f %s = %s$'%(latex((x0,y0)),latex(exact_value_ori))))
  pretty_print(html(r'Shifted point $%s$'%latex(((x0+deltax),(y0+deltay)))))
  pretty_print(html(r'Value of the function in shifted point is $%s$'%f(x0+deltax,y0+deltay)))
  pretty_print(html(r'Value on the tangent plane in shifted point is $%s$'%latex(approx_value)))
  pretty_print(html(r'Error is $%s$'%latex(abs_error)))
Line 1178: Line 1241:
{{{ {{{#!sagecell
Line 1206: Line 1269:
    html('$F(x,y) = e^{-(x^2+y^2)/2} \\cos(y) \\sin(x^2+y^2)$')     pretty_print(html('$F(x,y) = e^{-(x^2+y^2)/2} \\cos(y) \\sin(x^2+y^2)$'))
Line 1216: Line 1279:
http://www.sagenb.org/home/pub/2829/

{{{		 https://cloud.sagemath.com/projects/19575ea0-317e-402b-be57-368d04c113db/files/pub/2801-2901/2829.sagews

{{{#!sagecell
Line 1319: Line 1382:
== Lateral Surface Area == == Lateral Surface Area (FIXME in Jupyter) ==
Line 1323: Line 1386:
http://www.sagenb.org/home/pub/2826/

{{{		 http://sagenb.mc.edu/home/pub/89/

{{{#!sagecell
Line 1330: Line 1393:
##
Line 1332: Line 1396:
@interact
def _(f=input_box(default=6-4*x^2-y^2*2/5,label='$f(x,y) = $'),
        g=input_box(default=-2+sin(x)+sin(y),label='$g(x,y) = $'),
        u=input_box(default=cos(t),label='$u(t) = $'),
        v=input_box(default=2*sin(t),label='$v(t) = $'),
        a=input_box(default=0,label='$a = $'),
        b=input_box(default=3*pi/2,label='$b = $'),		 @interact(layout=dict(top=[['f','u'],['g','v']],
left=[['a'],['b'],['in_3d'],['smoother']],
bottom=[['xx','yy']]))
def _(f=input_box(default=6-4*x^2-y^2*2/5,label='Top = $f(x,y) = $',width=30),
        g=input_box(default=-2+sin(x)+sin(y),label='Bottom = $g(x,y) = $',width=30),
        u=input_box(default=cos(t),label='   $ x = u(t) = $',width=20),
        v=input_box(default=2*sin(t),label='   $ y = v(t) = $',width=20),
        a=input_box(default=0,label='$a = $',width=10),
        b=input_box(default=3*pi/2,label='$b = $',width=10),
Line 1341: Line 1407:
        smoother=checkbox(default=false)):         in_3d = checkbox(default=true,label='3D'),
 smoother=checkbox(default=false),
        auto_update=true):
Line 1343: Line 1411:
    ds = sqrt(derivative(u(t),t)^2+derivative(v(t),t)^2)     ds = sqrt(derivative(u,t)^2+derivative(v,t)^2)
Line 1347: Line 1415:
    A = (f(x=u(t),y=v(t))-g(x=u(t),y=v(t)))*ds.simplify_trig().simplify()     A = (f(x=u,y=v)-g(x=u,y=v))*ds.simplify_trig().simplify()
Line 1352: Line 1420:
    line_integral = integral(A,t,a,b) # If you want Sage to try, uncomment the lines below.

# line_integral = integrate(A,t,a,b)
# html(r'<align=center size=+1>Lateral Surface Area = $ %s $ </font>'%latex(line_integral))
Line 1354: Line 1426:
       
    html(r'<h4 align=center>Lateral Surface Area = $ %s $ </h4>'%latex(line_integral))

    html(r'<h4 align=center>Lateral Surface $ \approx $ %s</h2>'%str(line_integral_approx))
    pretty_print(html(r'<font align=center size=+1>Lateral Surface $ \approx $ %s</font>'%str(line_integral_approx)))
Line 1364: Line 1434:
    G += parametric_plot3d([u,v,g(x=u(t),y=v(t))],(t,a,b),thickness=2,color='red')
    G += parametric_plot3d([u,v,f(x=u(t),y=v(t))],(t,a,b),thickness=2,color='red')		     G += parametric_plot3d([u,v,g(x=u,y=v)],(t,a,b),thickness=2,color='red')
    G += parametric_plot3d([u,v,f(x=u,y=v)],(t,a,b),thickness=2,color='red')
Line 1374: Line 1444:
        G += parametric_plot3d([u(w),v(w),s*f(x=u(w),y=v(w))+(1-s)*g(x=u(w),y=v(w))],(s,0,1),thickness=lat_thick,color='yellow',opacity=0.9)
    show(G,spin=true)		         G += parametric_plot3d([u(t=w),v(t=w),s*f(x=u(t=w),y=v(t=w))+(1-s)*g(x=u(t=w),y=v(t=w))],(s,0,1),thickness=lat_thick,color='yellow',opacity=0.9)
             if in_3d:
        show(G,stereo='redcyan',spin=true)
    else:
        show(G,perspective_depth=true,spin=true)
Line 1380: Line 1454:
== Parametric surface example == == Parametric surface example (FIXME in Jupyter) ==
Line 1382: Line 1456:
{{{ {{{#!sagecell
Line 1401: Line 1475:
http://www.sagenb.org/home/pub/2827/

{{{		 https://cloud.sagemath.com/projects/19575ea0-317e-402b-be57-368d04c113db/files/pub/2801-2901/2827-$%20%5Cint_%7BC%7D%20%5Cleft%20%5Clangle%20M,N,P%20%5Cright%20%5Crangle%20dr%20$%20=%20$%20%25s%20$.sagews

{{{#!sagecell
Line 1437: Line 1511:
    html(r'<h2 align=center>$ \int_{C} \left \langle M,N,P \right \rangle dr $ = $ %s $ </h2>'%latex(line_integral))     pretty_print(html(r'<h2 align=center>$ \int_{C} \left \langle M,N,P \right \rangle dr $ = $ %s $ </h2>'%latex(line_integral)))

Sage Interactions - Calculus

goto interact main page

Contents

  1. Sage Interactions - Calculus
    1. Root Finding Using Bisection
    2. Newton's Method
    3. A contour map and 3d plot of two inverse distance functions
    4. A simple tangent line grapher
    5. Numerical integrals with the midpoint rule
    6. Numerical integrals with various rules
    7. Some polar parametric curves
    8. Function tool
    9. Newton-Raphson Root Finding
    10. Coordinate Transformations (FIXME in Jupyter)
    11. Taylor Series
    12. Illustration of the precise definition of a limit
    13. A graphical illustration of sin(x)/x -> 1 as x-> 0
    14. Quadric Surface Plotter
    15. The midpoint rule for numerically integrating a function of two variables
    16. Gaussian (Legendre) quadrature
    17. Vector Calculus, 2-D Motion
    18. Vector Calculus, 3-D Motion (FIXME)
    19. Multivariate Limits by Definition
    20. Directional Derivatives
    21. 3D graph with points and curves
    22. Approximating function in two variables by differential
    23. Taylor approximations in two variables
    24. Volumes over non-rectangular domains
    25. Lateral Surface Area (FIXME in Jupyter)
    26. Parametric surface example (FIXME in Jupyter)
    27. Line Integrals in 3D Vector Field

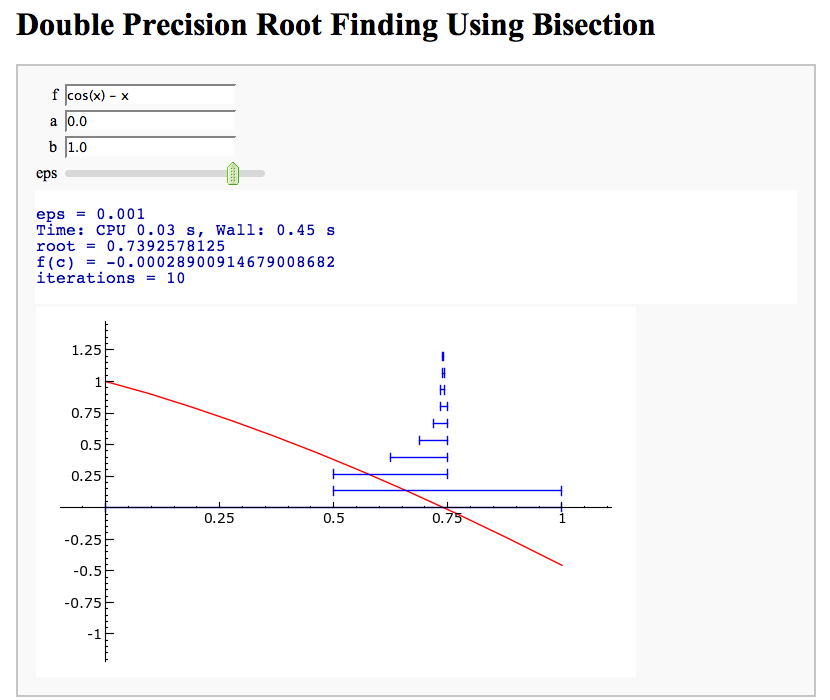
Root Finding Using Bisection

by William Stein

bisect.png

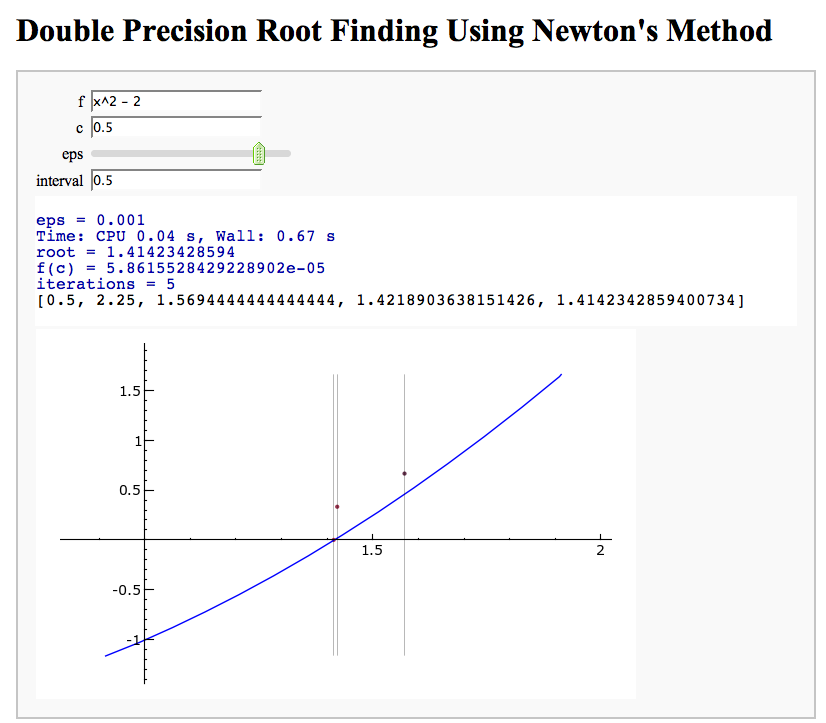
Newton's Method

Note that there is a more complicated Newton's method below.

by William Stein

https://cloud.sagemath.com/projects/19575ea0-317e-402b-be57-368d04c113db/files/pub/2801-2901/2824-Double%20Precision%20Root%20Finding%20Using%20Newton's%20Method.sagews

newton.png

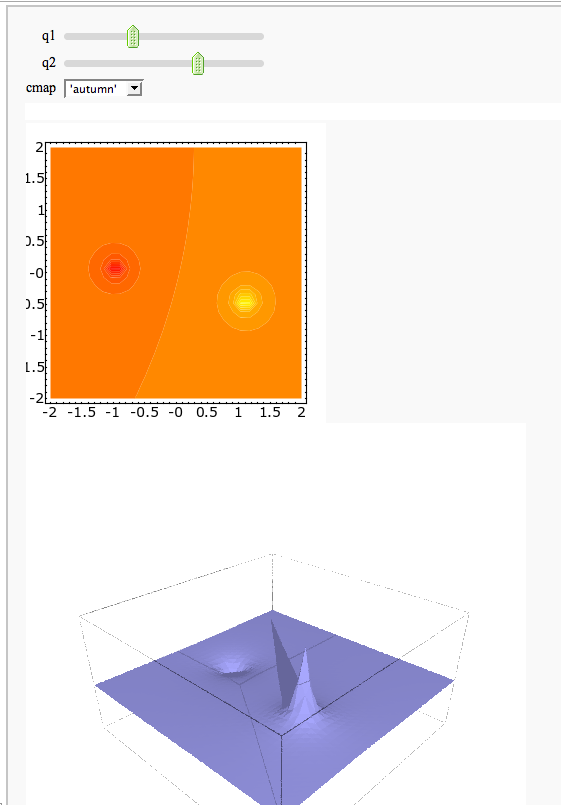
A contour map and 3d plot of two inverse distance functions

by William Stein

https://cloud.sagemath.com/projects/19575ea0-317e-402b-be57-368d04c113db/files/pub/2801-2901/2823.sagews

mountains.png

A simple tangent line grapher

by Marshall Hampton

tangents.png

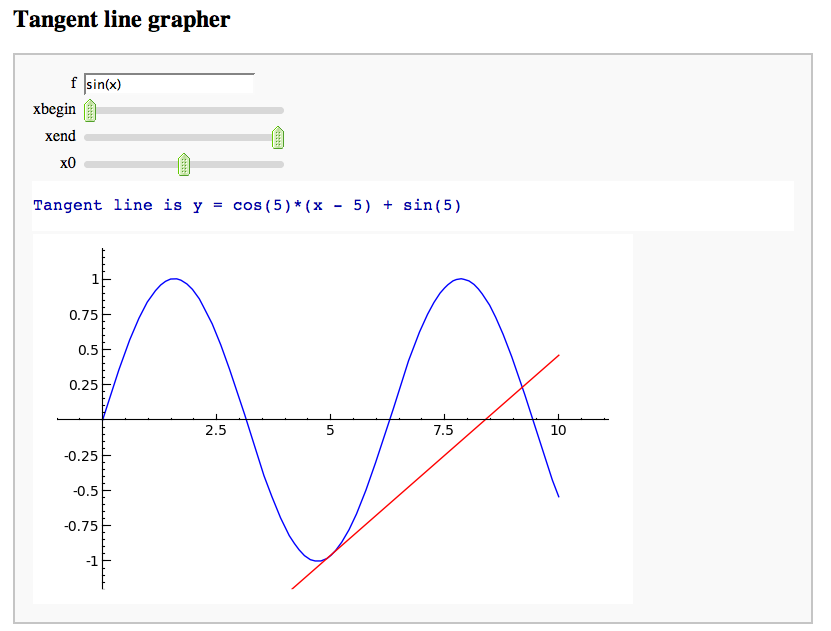
Numerical integrals with the midpoint rule

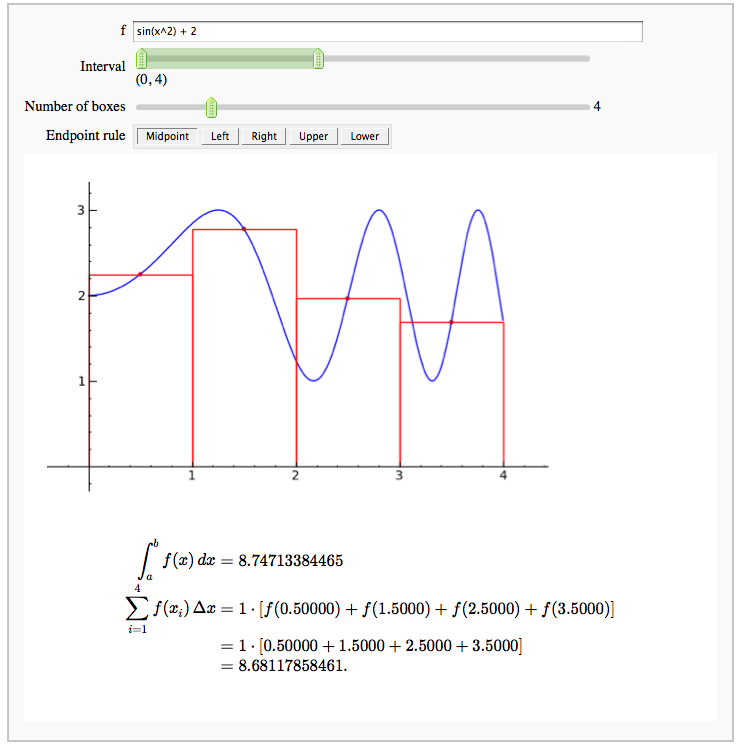
by Marshall Hampton

num_int.png

Numerical integrals with various rules

by Nick Alexander (based on the work of Marshall Hampton)

{{{#!sagecellvar('x') @interact def midpoint(f = input_box(default = sin(x^2) + 2, type = SR),

  • interval=range_slider(0, 10, 1, default=(0, 4), label="Interval"), number_of_subdivisions = slider(1, 20, 1, default=4, label="Number of boxes"), endpoint_rule = selector(['Midpoint', 'Left', 'Right', 'Upper', 'Lower'], nrows=1, label="Endpoint rule")): a, b = map(QQ, interval) t = var('t') func = fast_callable(f(x=t), RDF, vars=[t]) dx = ZZ(b-a)/ZZ(number_of_subdivisions) xs = [] ys = [] for q in range(number_of_subdivisions):
    • if endpoint_rule == 'Left':
      • xs.append(q*dx + a)
      elif endpoint_rule == 'Midpoint':
      • xs.append(q*dx + a + dx/2)
      elif endpoint_rule == 'Right':
      • xs.append(q*dx + a + dx)
      elif endpoint_rule == 'Upper':
      • x = find_local_maximum(func, q*dx + a, q*dx + dx + a)[1] xs.append(x)
      elif endpoint_rule == 'Lower':
      • x = find_local_minimum(func, q*dx + a, q*dx + dx + a)[1] xs.append(x)
    ys = [ func(x) for x in xs ] rects = Graphics() for q in range(number_of_subdivisions): min_y = min(0, find_local_minimum(func,a,b)[0]) max_y = max(0, find_local_maximum(func,a,b)[0])

    # html('<h3>Numerical integrals with the midpoint rule</h3>') show(plot(func,a,b) + rects, xmin = a, xmax = b, ymin = min_y, ymax = max_y) def cap(x):

    • # print only a few digits of precision

      if x < 1e-4:

      • return 0

      return RealField(20)(x)

    sum_html = "%s \cdot \\left[ %s \\right]" % (dx, ' + '.join([ "f(%s)" % cap(i) for i in xs ])) num_html = "%s \cdot \\left[ %s \\right]" % (dx, ' + '.join([ str(cap(i)) for i in ys ])) numerical_answer = integral_numerical(func,a,b,max_points = 200)[0] estimated_answer = dx * sum([ ys[q] for q in range(number_of_subdivisions)])

    pretty_print(html(r <div class="math"> \begin{align*} \int_{a}^{b} {f(x) \, dx} & = %s \\\ \sum_{i=1}^{%s} {f(x_i) \, \Delta x} & = %s \\\ & = %s \\\ & = %s . \end{align*} </div>

    • % (numerical_answer, number_of_subdivisions, sum_html, num_html, estimated_answer)))

}}} num_int2.png

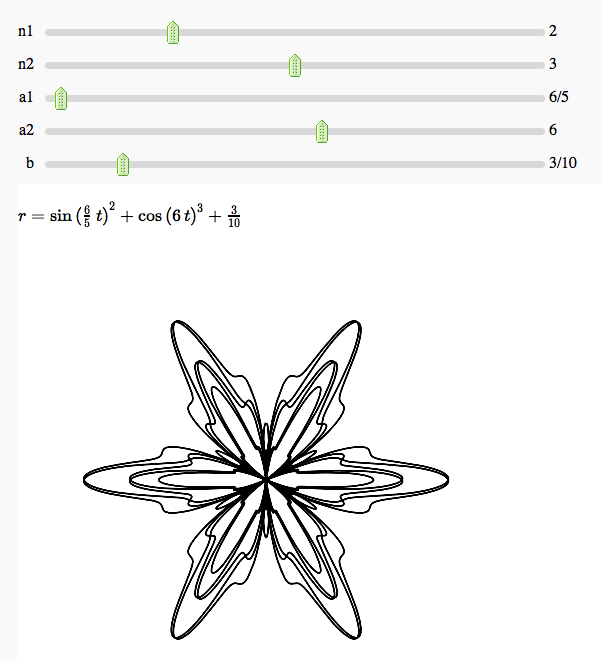
Some polar parametric curves

by Marshall Hampton. This is not very general, but could be modified to show other families of polar curves.

polarcurves1.png

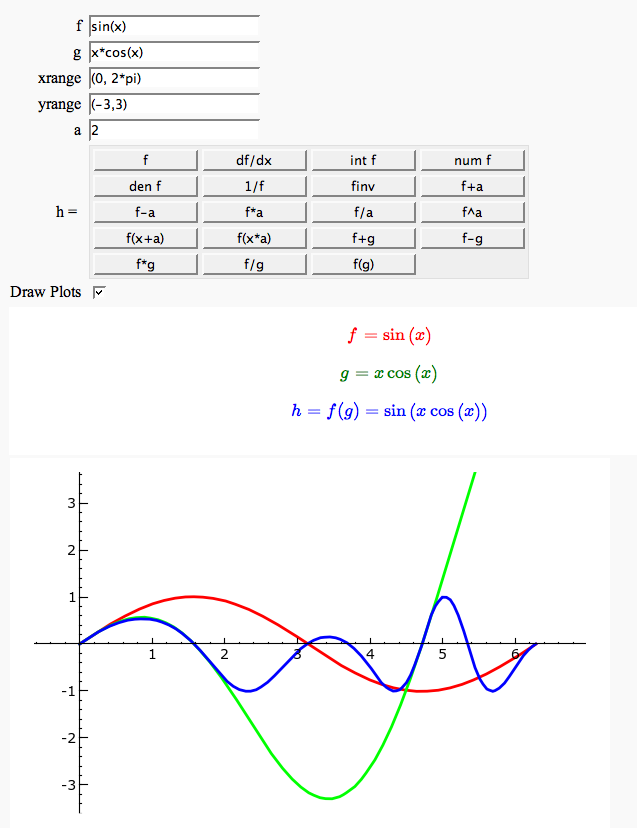
Function tool

Enter symbolic functions f, g, and a, a range, then click the appropriate button to compute and plot some combination of f, g, and a along with f and g. This is inspired by the Matlab funtool GUI.

funtool.png

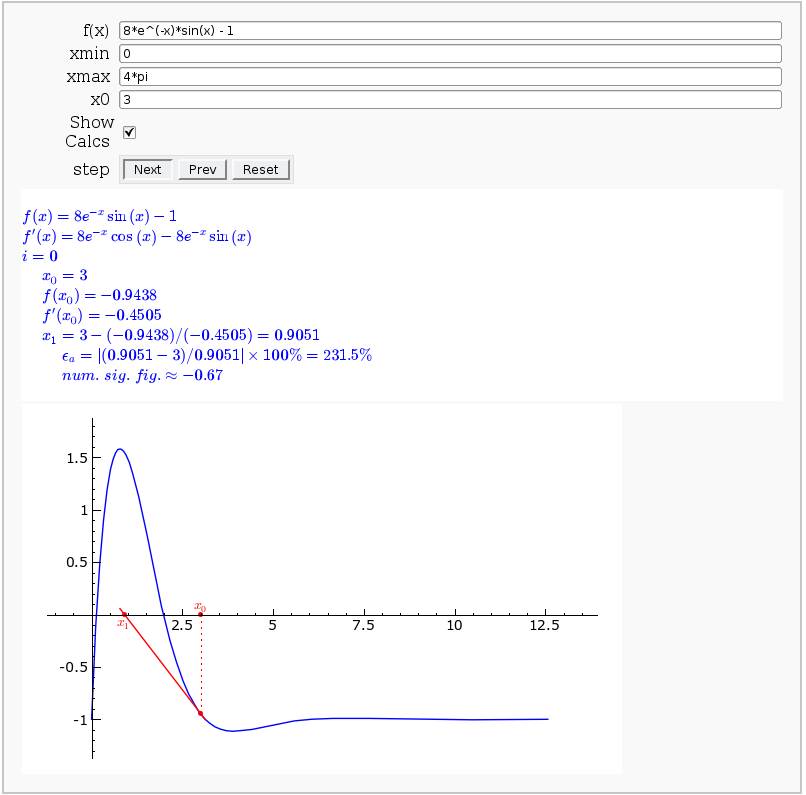
Newton-Raphson Root Finding

by Neal Holtz

This allows user to display the Newton-Raphson procedure one step at a time. It uses the heuristic that, if any of the values of the controls change, then the procedure should be re-started, else it should be continued.

newtraph.png

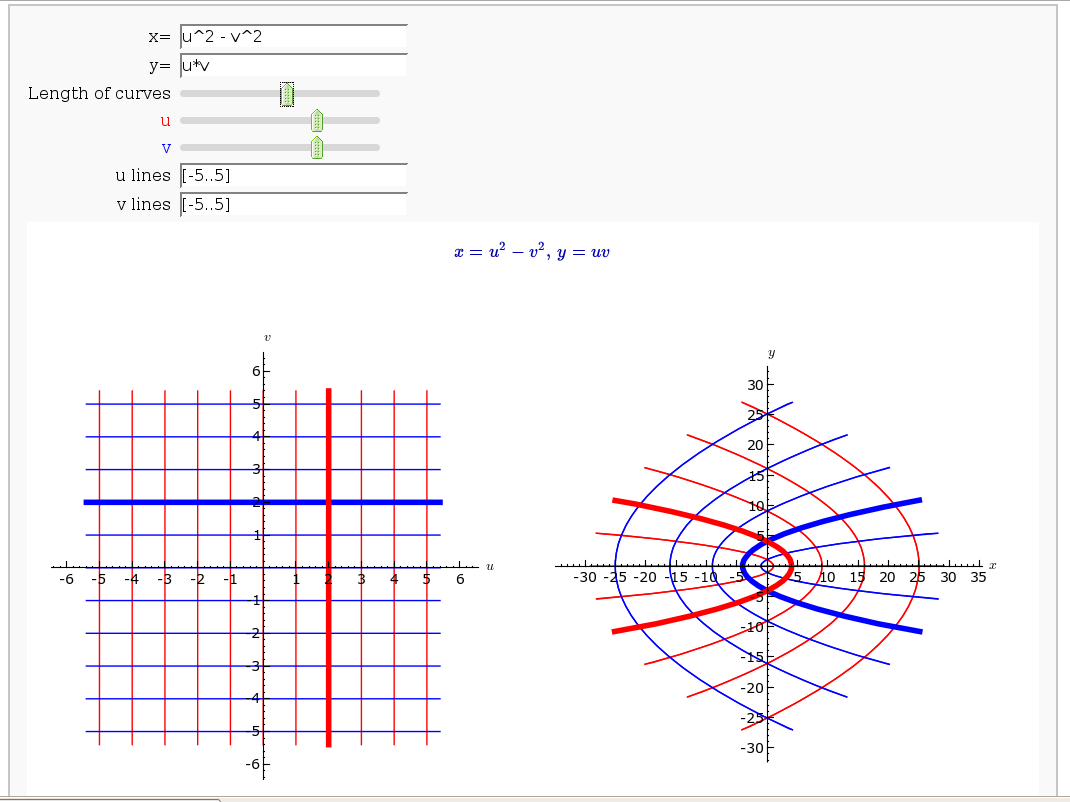
Coordinate Transformations (FIXME in Jupyter)

by Jason Grout

coordinate-transform-1.png coordinate-transform-2.png

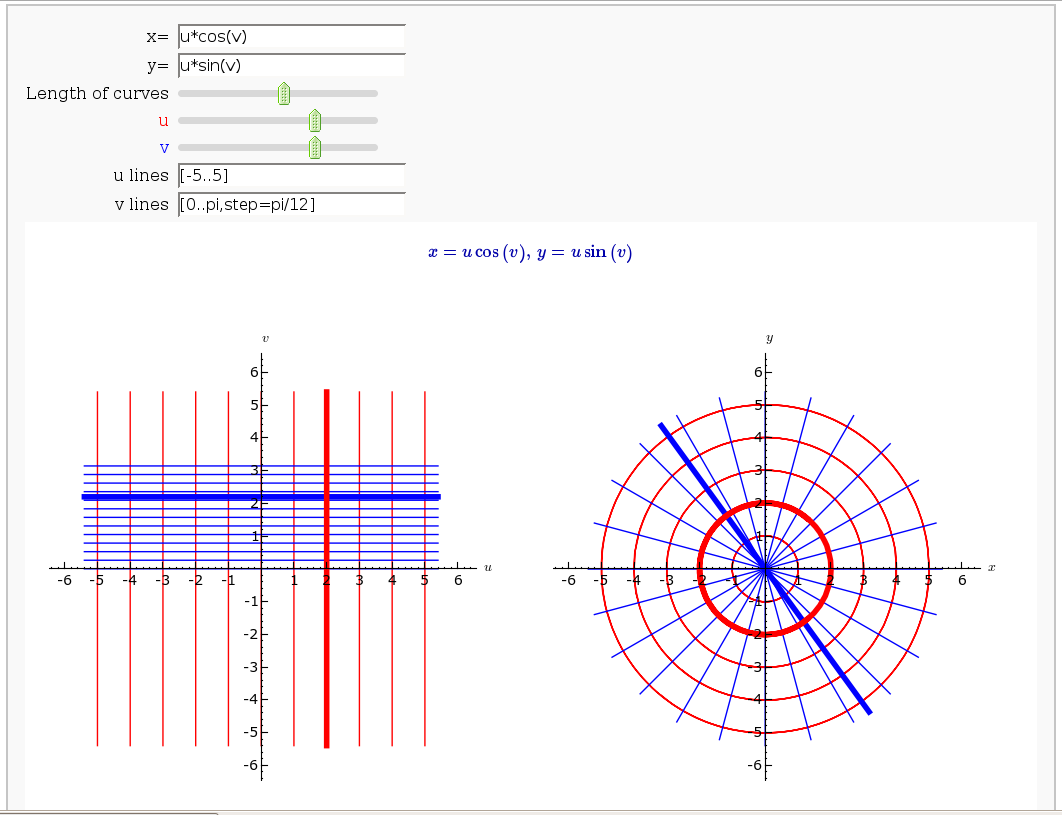
Taylor Series

by Harald Schilly

taylor_series_animated.gif

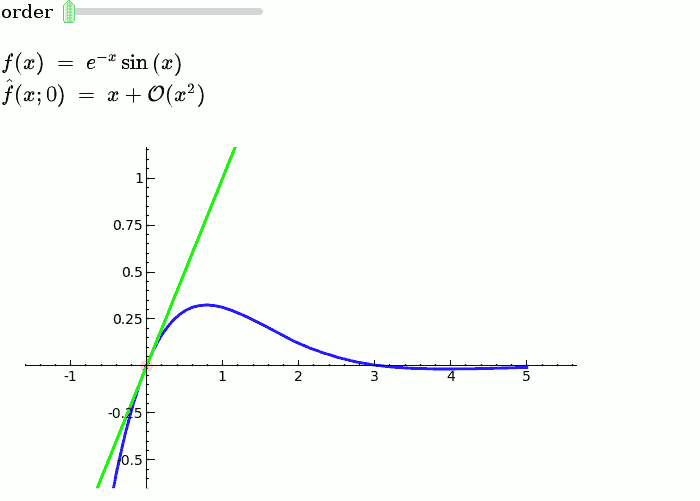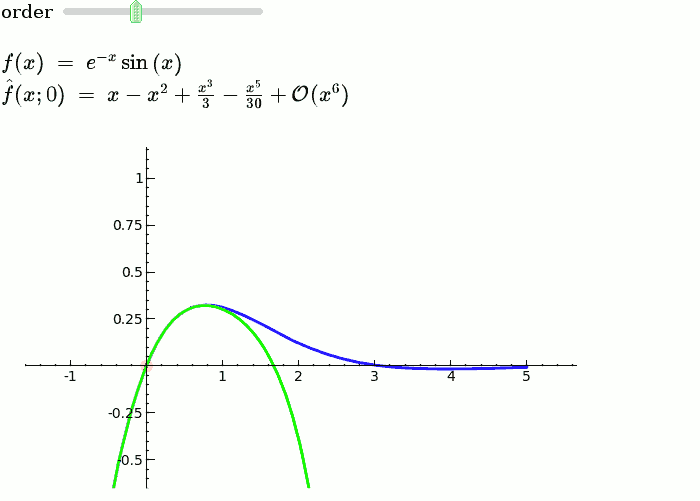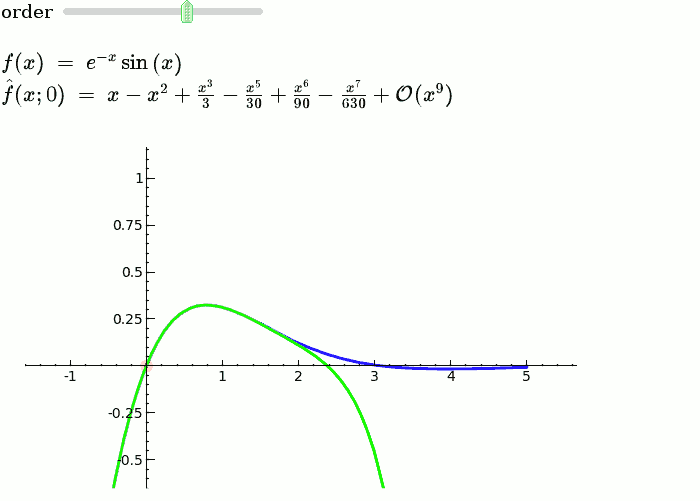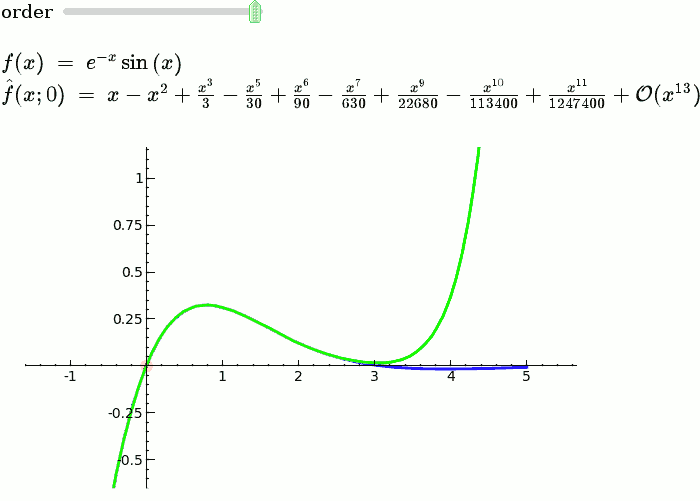
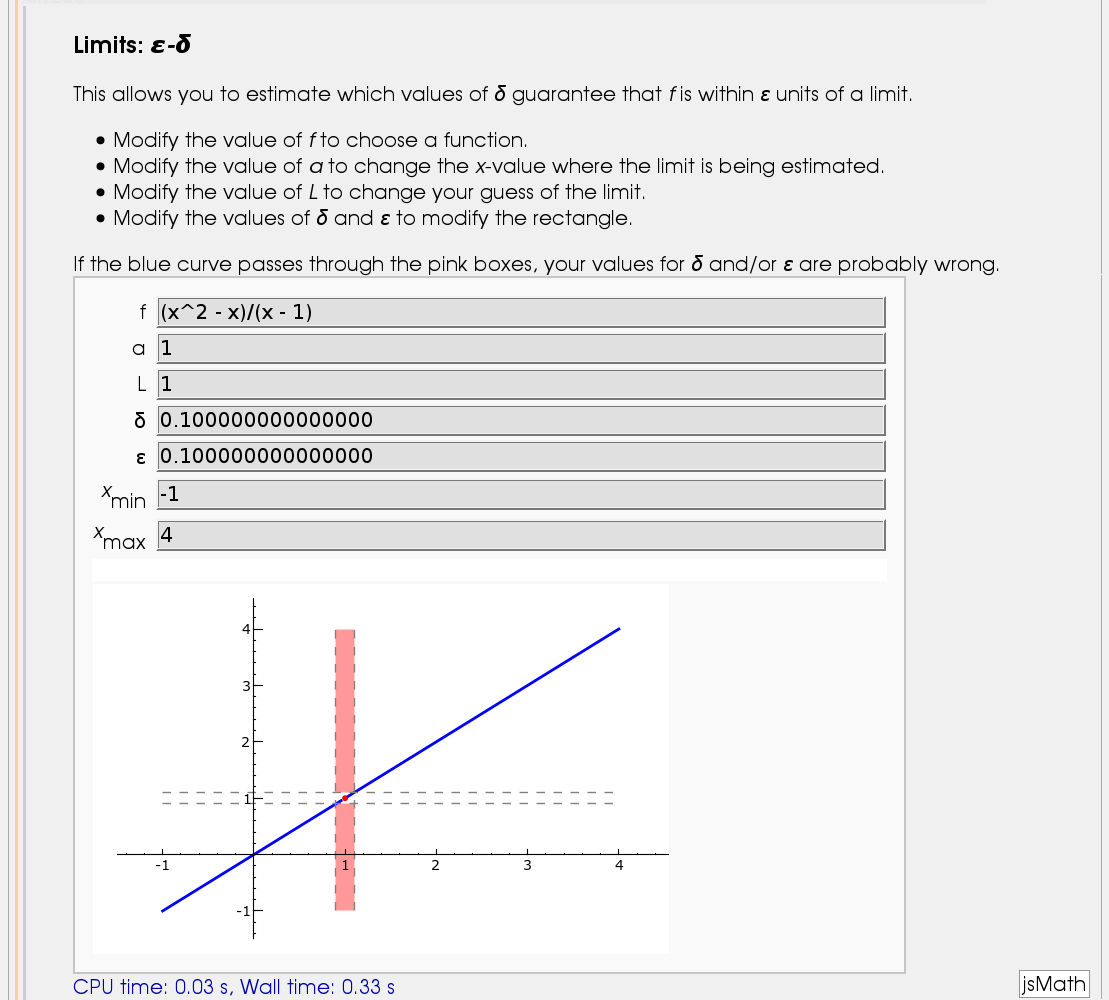
Illustration of the precise definition of a limit

by John Perry

I'll break tradition and put the image first. Apologies if this is Not A Good Thing.

snapshot_epsilon_delta.png

A graphical illustration of sin(x)/x -> 1 as x-> 0

by Wai Yan Pong

sinelimit.png

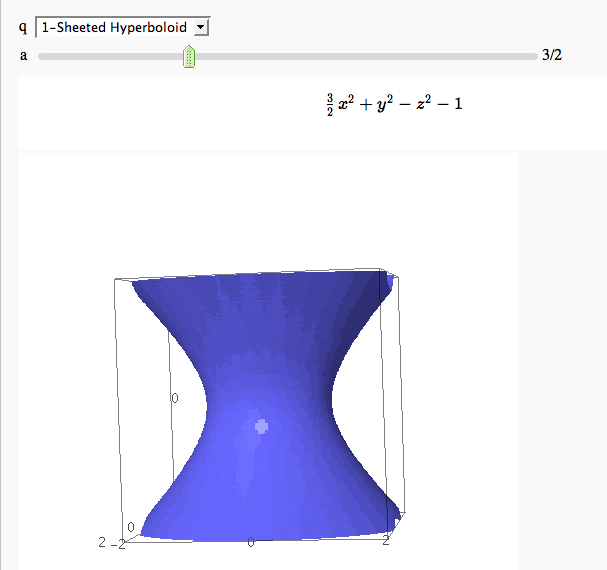
Quadric Surface Plotter

by Marshall Hampton. This is pretty simple, so I encourage people to spruce it up. In particular, it isn't set up to show all possible types of quadrics.

quadrics.png

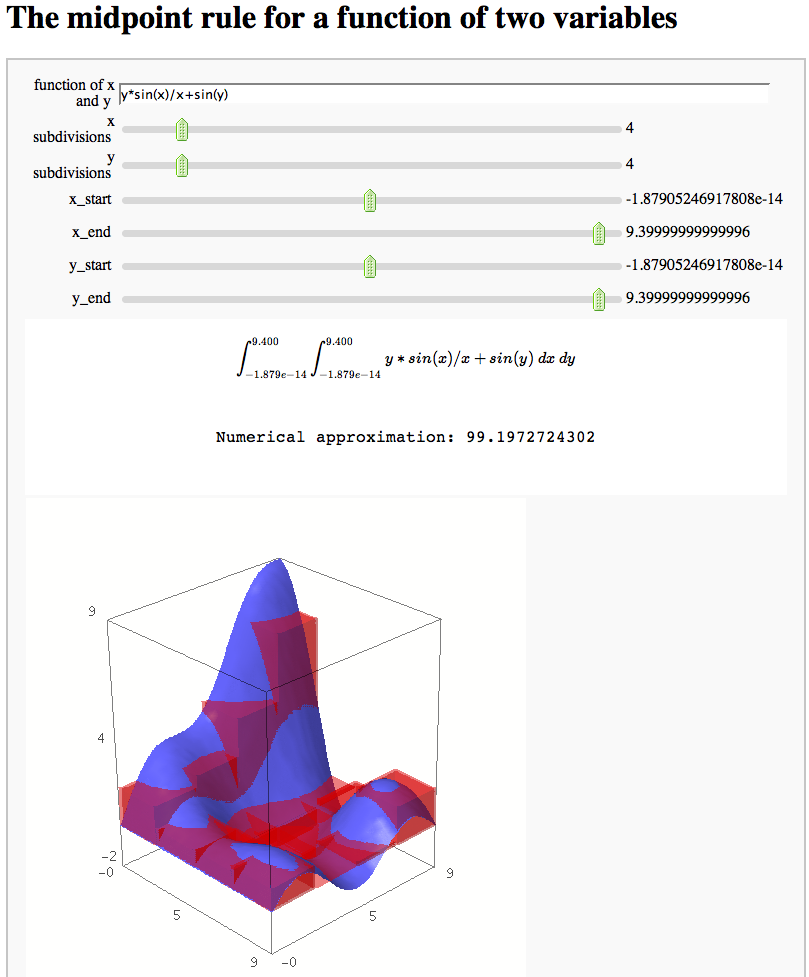
The midpoint rule for numerically integrating a function of two variables

by Marshall Hampton

numint2d.png

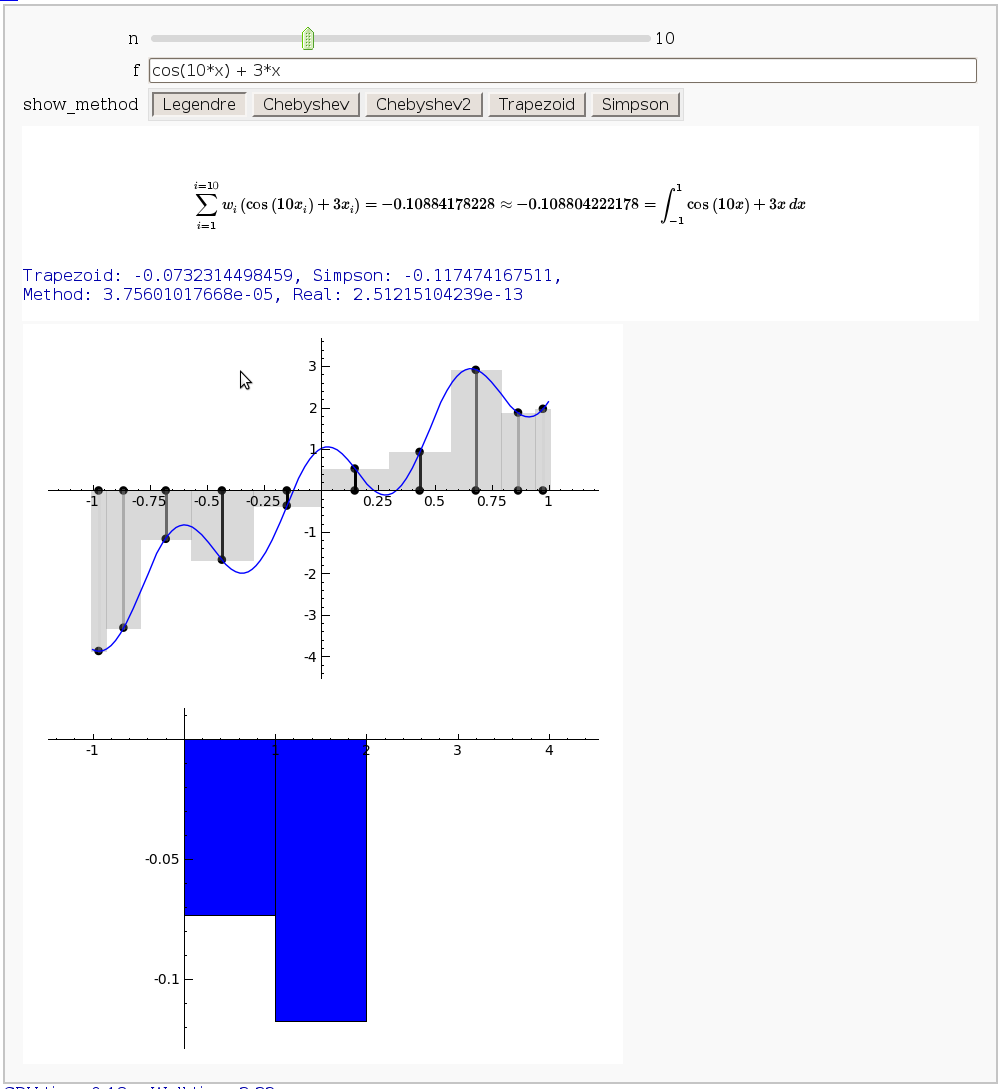
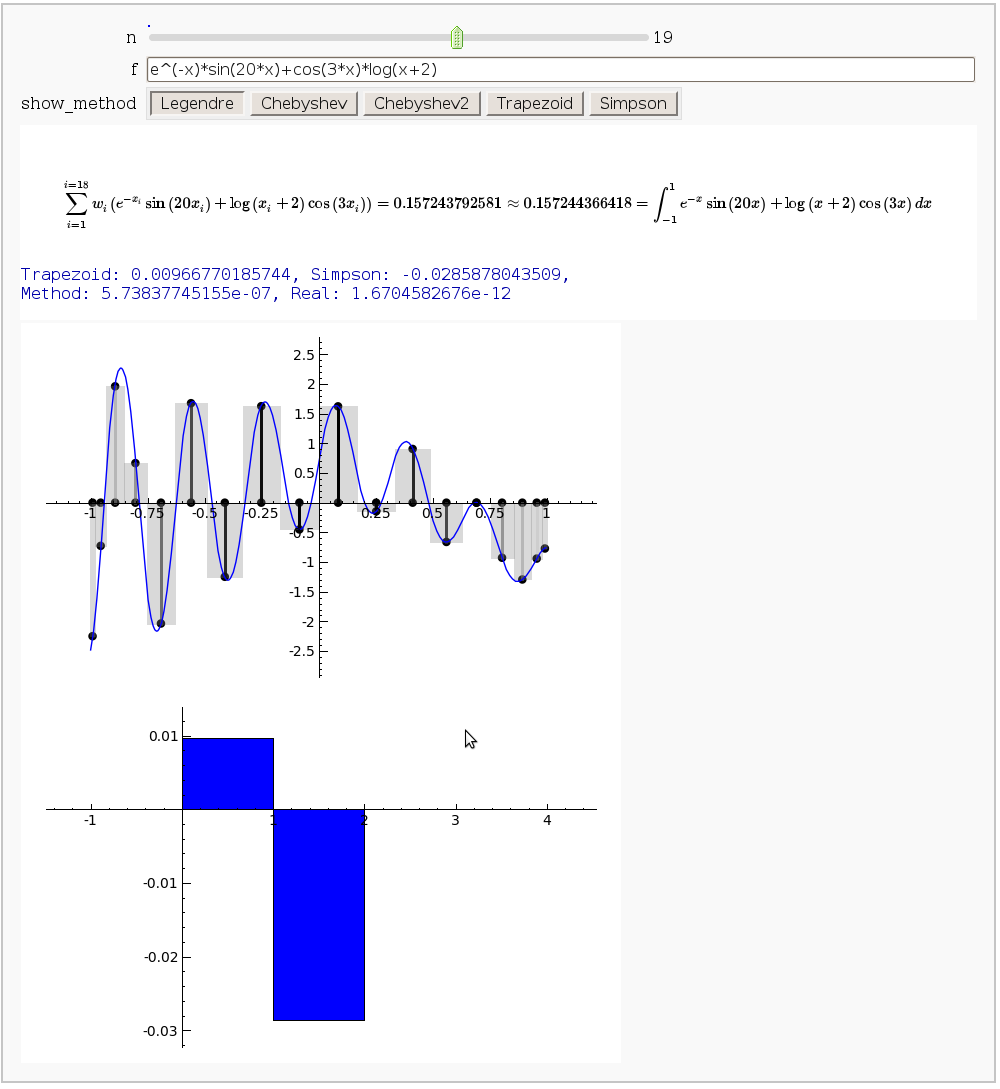
Gaussian (Legendre) quadrature

by Jason Grout

The output shows the points evaluated using Gaussian quadrature (using a weight of 1, so using Legendre polynomials). The vertical bars are shaded to represent the relative weights of the points (darker = more weight). The error in the trapezoid, Simpson, and quadrature methods is both printed out and compared through a bar graph. The "Real" error is the error returned from scipy on the definite integral.

quadrature1.png quadrature2.png

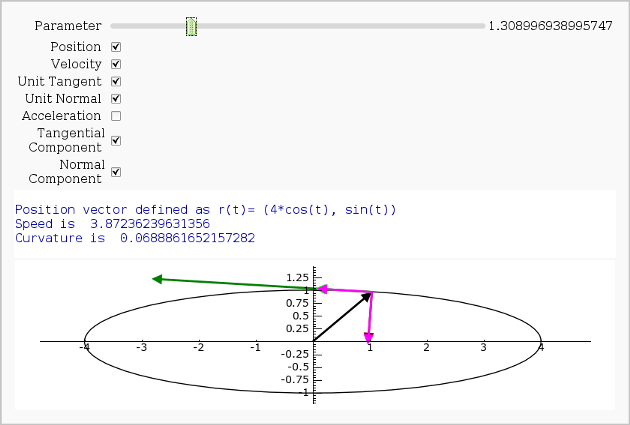
Vector Calculus, 2-D Motion

By Rob Beezer

A fast_float() version is available in a worksheet

motion2d.png

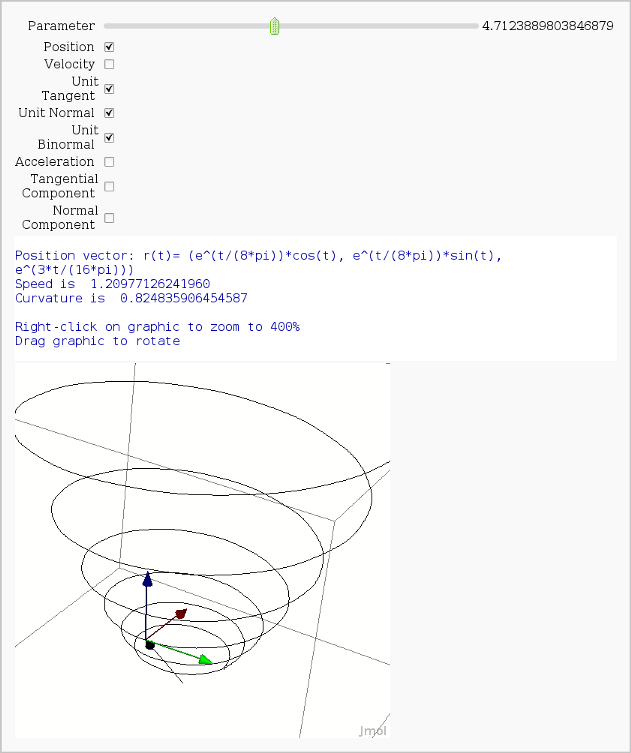
Vector Calculus, 3-D Motion (FIXME)

by Rob Beezer

Available as a worksheet

motion3d.png

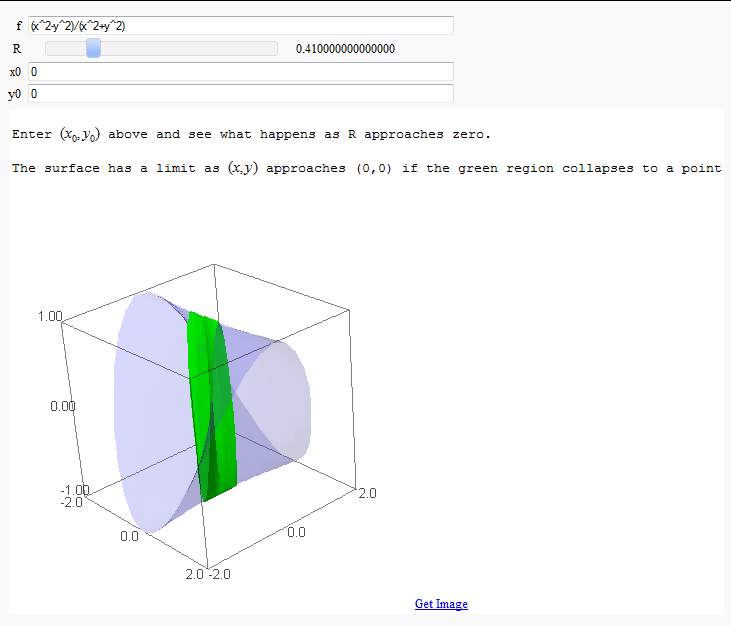
Multivariate Limits by Definition

by John Travis

http://sagenb.mc.edu/home/pub/97/

3D_Limit_Defn.png

3D_Limit_Defn_Contours.png

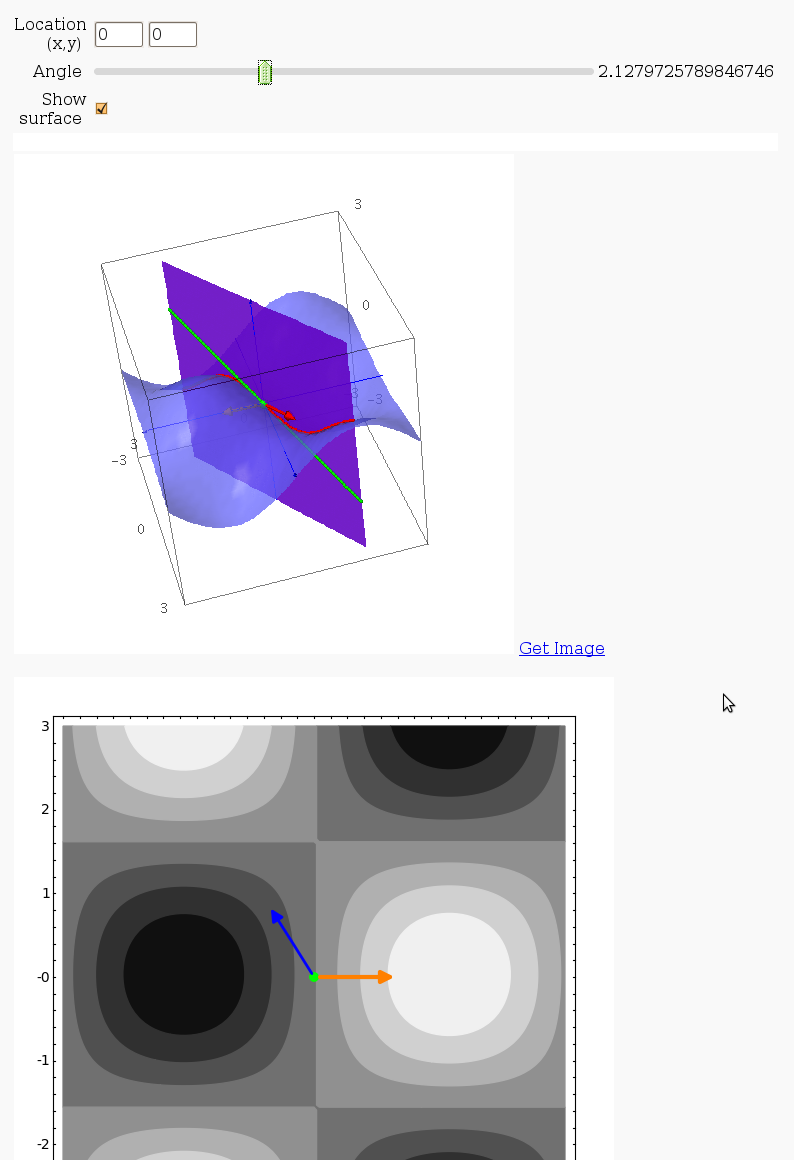
Directional Derivatives

This interact displays graphically a tangent line to a function, illustrating a directional derivative (the slope of the tangent line).

directional derivative.png

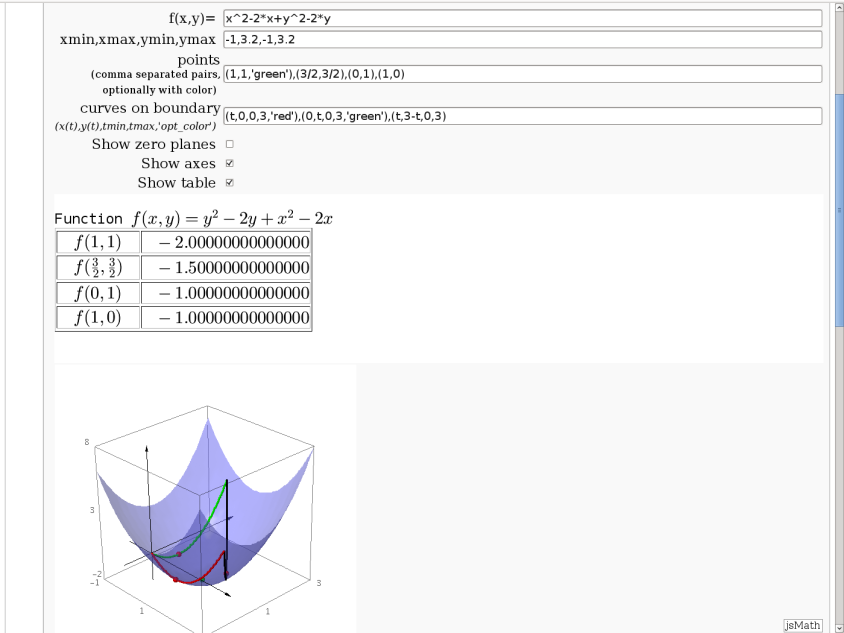
3D graph with points and curves

By Robert Marik

This sagelet is handy when showing local, constrained and absolute maxima and minima in two variables. Available as a worksheet

3Dgraph_with_points.png

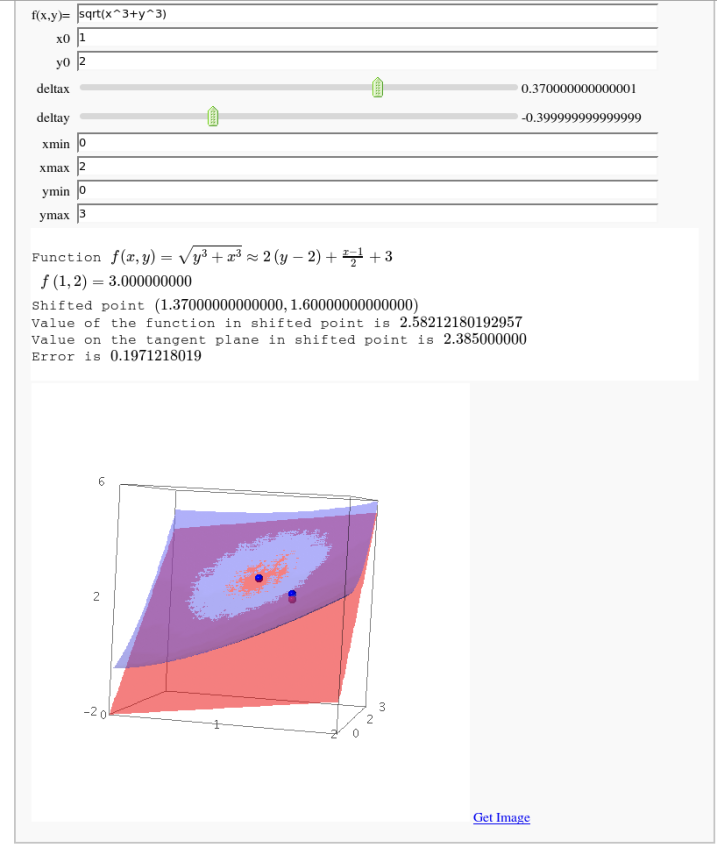
Approximating function in two variables by differential

by Robert Marik

3D_differential.png

Taylor approximations in two variables

by John Palmieri

This displays the nth order Taylor approximation, for n from 1 to 10, of the function sin(x2 + y2) cos(y) exp(-(x2+y2)/2).

taylor-3d.png

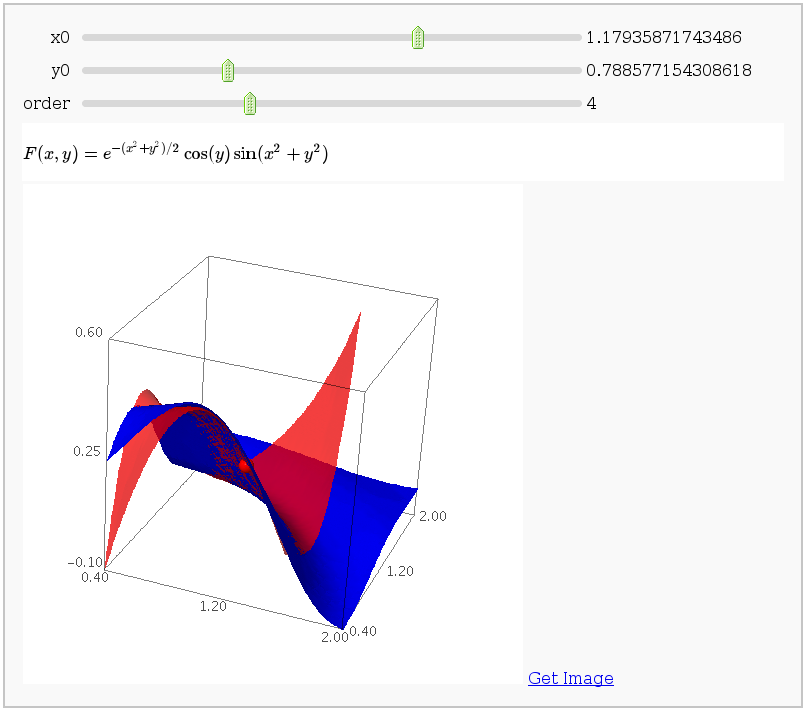
Volumes over non-rectangular domains

by John Travis

https://cloud.sagemath.com/projects/19575ea0-317e-402b-be57-368d04c113db/files/pub/2801-2901/2829.sagews

3D_Irregular_Volume.png

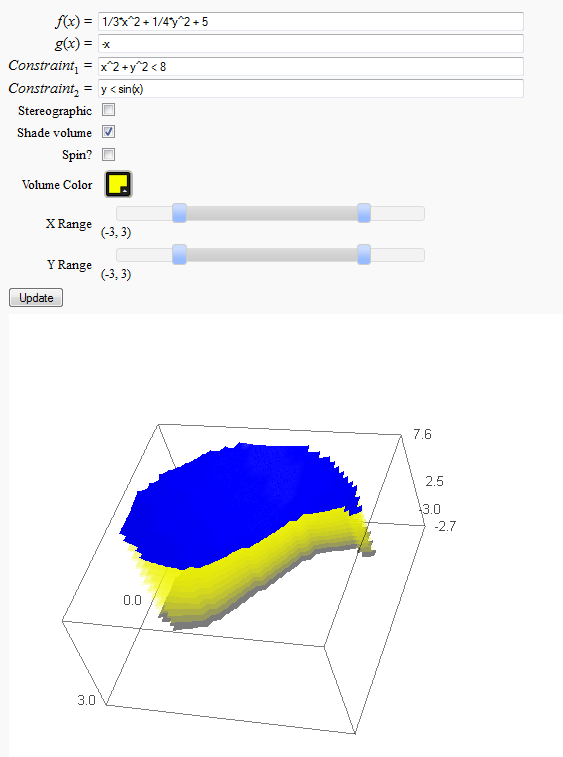
Lateral Surface Area (FIXME in Jupyter)

by John Travis

http://sagenb.mc.edu/home/pub/89/

Lateral_Surface.png

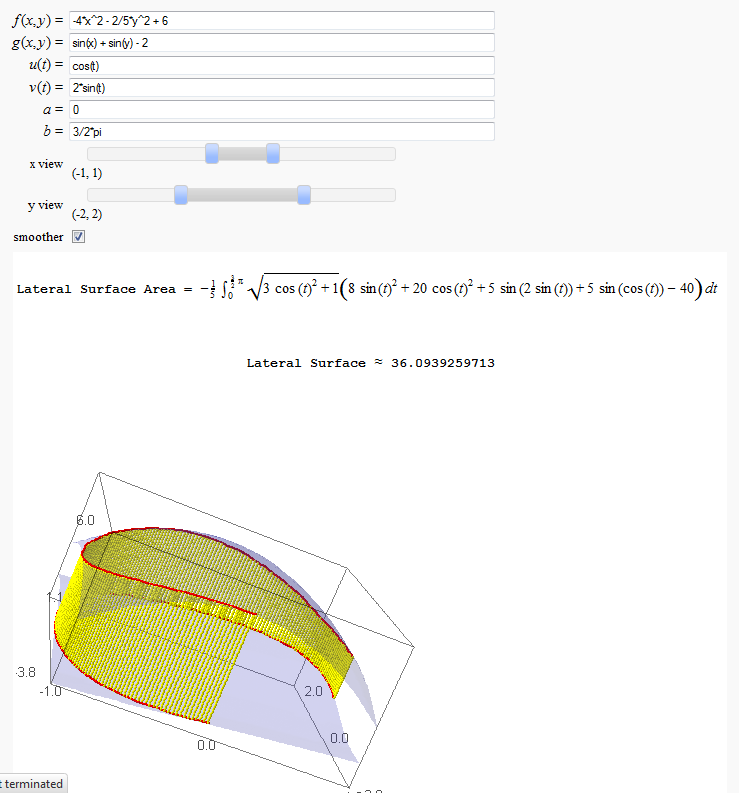
Parametric surface example (FIXME in Jupyter)

by Marshall Hampton

parametric_surface.png

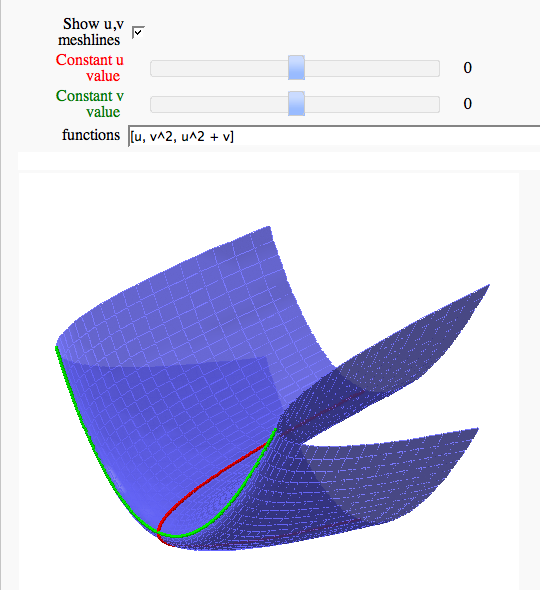
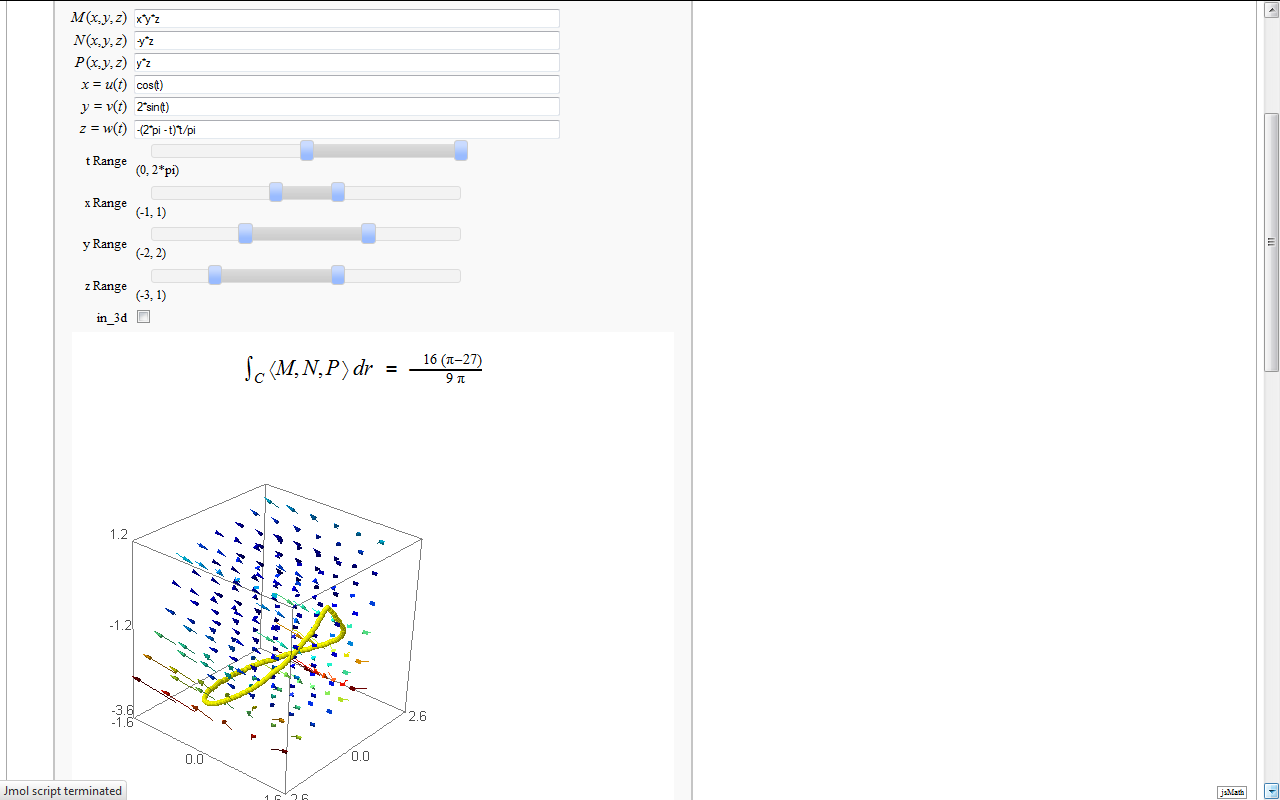
Line Integrals in 3D Vector Field

by John Travis

https://cloud.sagemath.com/projects/19575ea0-317e-402b-be57-368d04c113db/files/pub/2801-2901/2827-$%20%5Cint_%7BC%7D%20%5Cleft%20%5Clangle%20M,N,P%20%5Cright%20%5Crangle%20dr%20$%20=%20$%20%25s%20$.sagews

3D_Line_Integral.png

interact/calculus (last edited 2020-08-11 14:10:09 by kcrisman)