Differences between revisions 96 and 115 (spanning 19 versions)
⇤ ← Revision 96 as of 2017-03-18 16:17:41 →
Size: 62900
Editor: mforets
Comment: fix DeprecationWarning and badly displayed html in Quadric Surface Plotter
← Revision 115 as of 2020-06-02 15:03:42 → ⇥
Size: 63115
Editor: kcrisman
Comment:
Deletions are marked like this. Additions are marked like this.
Line 27: Line 27:
            raise ValueError, "f must have a sign change in the interval (%s,%s)"%(a,b)             raise ValueError("f must have a sign change in the interval (%s,%s)"%(a,b))
Line 33: Line 33:
     print "eps = %s"%float(eps)      print("eps = %s" % float(eps))
Line 37: Line 37:
         print "f must have opposite sign at the endpoints of the interval"          print("f must have opposite sign at the endpoints of the interval")
Line 40: Line 40:
         print "root =", c
         print "f(c) = %r"%f(x=c)
         print "iterations =", len(intervals)		          print("root =", c)
         print("f(c) = %r" % f(x=c))
         print("iterations =", len(intervals))
Line 69: Line 69:
    for i in xrange(maxiter):     for i in range(maxiter):
Line 81: Line 81:
     print "eps = %s"%float(eps)      print("eps = %s"%float(eps))
Line 83: Line 83:
     print "root =", z
     print "f(c) = %r"%f(x=z)		      print("root = {}".format(z))
     print("f(c) = %r" % f(x=z))
Line 86: Line 86:
     print "iterations =", n      print("iterations = {}".format(n))
Line 127: Line 127:
    print 'Tangent line is y = ' + tanf._repr_()     print('Tangent line is y = ' + tanf._repr_())
Line 155: Line 155:
    pretty_print(html('$\int_{a}^{b}{f(x) dx} {\\approx} \sum_i{f(x_i) \Delta x}$'))
    print "\n\nSage numerical answer: " + str(integral_numerical(func,a,b,max_points = 200)[0])
    print "Midpoint estimated answer: " + str(RDF(dx*sum([midys[q] for q in range(n)])))		     pretty_print(html(r'$\int_{a}^{b}{f(x) dx} {\approx} \sum_i{f(x_i) \Delta x}$'))
    print("\n\nSage numerical answer: " + str(integral_numerical(func,a,b,max_points = 200)[0]))
    print("Midpoint estimated answer: " + str(RDF(dx*sum([midys[q] for q in range(n)]))))
Line 257: Line 257:
    except TypeError, msg:
        print msg[-200:]
        print "Unable to make sense of f,g, or a as symbolic expressions."		     except TypeError as msg:
        print(msg[-200:])
        print("Unable to make sense of f,g, or a as symbolic expressions.")
Line 446: Line 446:
== Coordinate Transformations (FIXME in Jupyter) == == Coordinate Transformations ==
Line 466: Line 466:
         u_percent=slider(0,1,0.05,label="<font color='red'>u</font>", default=.7),
         v_percent=slider(0,1,0.05,label="<font color='blue'>v</font>", default=.7),		          u_percent=slider(0,1,0.05,label="u", default=.7),
         v_percent=slider(0,1,0.05,label="v", default=.7),
Line 497: Line 497:
    jacobian=abs(T.diff().det()).simplify_full()     jacobian(u,v)=abs(T.diff().det()).simplify_full()
Line 508: Line 508:
    pretty_print(table([[uvplot,xyplot]]))     show(graphics_array([uvplot,xyplot]))
Line 527: Line 527:
    pretty_print(html('$f(x)\;=\;%s$'%latex(f)))
    pretty_print(html('$\hat{f}(x;%s)\;=\;%s+\mathcal{O}(x^{%s})$'%(x0,latex(ft),order+1)))		     pretty_print(html(r'$f(x)\;=\;%s$'%latex(f)))
    pretty_print(html(r'$\hat{f}(x;%s)\;=\;%s+\mathcal{O}(x^{%s})$'%(x0,latex(ft),order+1)))
Line 571: Line 571:
    pretty_print(html('<h3>A graphical illustration of $\lim_{x -> 0} \sin(x)/x =1$</h3>'))
    pretty_print(html('Below is the unit circle, so the length of the <font color=red>red line</font> is |sin(x)|'))
    pretty_print(html('and the length of the <font color=blue>blue line</font> is |tan(x)| where x is the length of the arc.'))
    pretty_print(html('From the picture, we see that |sin(x)| $\le$ |x| $\le$ |tan(x)|.'))
    pretty_print(html('It follows easily from this that cos(x) $\le$ sin(x)/x $\le$ 1 when x is near 0.'))
    pretty_print(html('As $\lim_{x ->0} \cos(x) =1$, we conclude that $\lim_{x -> 0} \sin(x)/x =1$.'))		     pretty_print(html(r'<h3>A graphical illustration of $\lim_{x -> 0} \sin(x)/x =1$</h3>'))
    pretty_print(html(r'Below is the unit circle, so the length of the <font color=red>red line</font> is |sin(x)|'))
    pretty_print(html(r'and the length of the <font color=blue>blue line</font> is |tan(x)| where x is the length of the arc.'))
    pretty_print(html(r'From the picture, we see that |sin(x)| $\le$ |x| $\le$ |tan(x)|.'))
    pretty_print(html(r'It follows easily from this that cos(x) $\le$ sin(x)/x $\le$ 1 when x is near 0.'))
    pretty_print(html(r'As $\lim_{x ->0} \cos(x) =1$, we conclude that $\lim_{x -> 0} \sin(x)/x =1$.'))
Line 597: Line 597:
def quads(q = selector(quadrics.keys()), a = slider(0,5,1/2,default = 1)): def quads(q = selector(list(quadrics)), a = slider(0,5,1/2,default = 1)):
Line 628: Line 628:
pretty_print(html("<h1>The midpoint rule for a function of two variables</h1>")) pretty_print(html(r"<h1>The midpoint rule for a function of two variables</h1>"))
Line 643: Line 643:
    pretty_print(html("$$\int_{"+str(R16(y_start))+"}^{"+str(R16(y_end))+"} "+ "\int_{"+str(R16(x_start))+"}^{"+str(R16(x_end))+"} "+func+"\ dx \ dy$$"))
    pretty_print(html('<p style="text-align: center;">Numerical approximation: ' + str(num_approx)+'</p>'))		     pretty_print(html(r"$\int_{"+str(R16(y_start))+r"}^{"+str(R16(y_end))+r"} "+ r"\int_{"+str(R16(x_start))+r"}^{"+str(R16(x_end))+r"} "+latex(SR(func))+r"\ dx \ dy$"))
    pretty_print(html(r'<p style="text-align: center;">Numerical approximation: ' + str(num_approx)+r'</p>'))
Line 660: Line 660:
from numpy import linspace from numpy import linspace, asanyarray, diff
Line 712: Line 712:
    y_val = map(scaled_ff,x_val)     y_val = [*map(scaled_ff,x_val)]
Line 715: Line 715:
    pretty_print(html("$$\sum_{i=1}^{i=%s}w_i\left(%s\\right)= %s\\approx %s =\int_{-1}^{1}%s \,dx$$"%(n,     pretty_print(html(r"$$\sum_{i=1}^{i=%s}w_i\left(%s\right)= %s\approx %s =\int_{-1}^{1}%s \,dx$$"%(n,
Line 718: Line 718:
    print "Trapezoid: %s, Simpson: %s, \nMethod: %s, Real: %s"%tuple(error_data)     print("Trapezoid: %s, Simpson: %s, \nMethod: %s, Real: %s" % tuple(error_data))
Line 756: Line 756:
path = parametric_plot( position(t).list(), (t, start, stop), color = "black" ) path = parametric_plot( position.list(), (t, start, stop), color = "black" )
Line 760: Line 760:
velocity = derivative(position(t), t)
acceleration = derivative(velocity(t), t)		 velocity = derivative(position, t)
acceleration = derivative(velocity, t)
Line 765: Line 765:
dT = derivative(tangent(t), t) dT = derivative(tangent, t)
Line 786: Line 786:
    pos_tzero = position(t0)     pos_tzero = position(t=t0)
Line 790: Line 790:
    speed_component = speed(t0)
    tangent_component = speed_deriv(t0)
    normal_component = sqrt( acceleration(t0).norm()^2 - tangent_component^2 )		     speed_component = speed(t=t0)
    tangent_component = speed_deriv(t=t0)
    normal_component = sqrt( acceleration(t=t0).norm()^2 - tangent_component^2 )
Line 798: Line 798:
    tan = arrow(pos_tzero, pos_tzero + tangent(t0), rgbcolor=(0,1,0) )
    vel = arrow(pos_tzero, pos_tzero + velocity(t0), rgbcolor=(0,0.5,0))
    nor = arrow(pos_tzero, pos_tzero + normal(t0), rgbcolor=(0.5,0,0))
    acc = arrow(pos_tzero, pos_tzero + acceleration(t0), rgbcolor=(1,0,1))
    tancomp = arrow(pos_tzero, pos_tzero + tangent_component*tangent(t0), rgbcolor=(1,0,1) )
    norcomp = arrow(pos_tzero, pos_tzero + normal_component*normal(t0), rgbcolor=(1,0,1))		     tan = arrow(pos_tzero, pos_tzero + tangent(t=t0), rgbcolor=(0,1,0) )
    vel = arrow(pos_tzero, pos_tzero + velocity(t=t0), rgbcolor=(0,0.5,0))
    nor = arrow(pos_tzero, pos_tzero + normal(t=t0), rgbcolor=(0.5,0,0))
    acc = arrow(pos_tzero, pos_tzero + acceleration(t=t0), rgbcolor=(1,0,1))
    tancomp = arrow(pos_tzero, pos_tzero + tangent_component*tangent(t=t0), rgbcolor=(1,0,1) )
    norcomp = arrow(pos_tzero, pos_tzero + normal_component*normal(t=t0), rgbcolor=(1,0,1))
Line 825: Line 825:
    print "Position vector defined as r(t)=", position(t)
    print "Speed is ", N(speed(t0))
    print "Curvature is ", N(curvature)		     print("Position vector defined as r(t)={}".format(position))
    print("Speed is {}".format(N(speed(t=t0))))
    print("Curvature is {}".format(N(curvature)))
Line 836: Line 836:
== Vector Calculus, 3-D Motion (FIXME) == == Vector Calculus, 3-D Motion ==
Line 857: Line 857:
assume(t, 'real')
Line 874: Line 875:
path = parametric_plot3d( position(t).list(), (t, start, stop), color = "black" ) path = parametric_plot3d( position.list(), (t, start, stop), color = "black" )
Line 878: Line 879:
velocity = derivative( position(t), t)
acceleration = derivative(velocity(t), t)		 velocity = derivative( position, t)
acceleration = derivative(velocity, t)
Line 883: Line 884:
dT = derivative(tangent(t), t) dT = derivative(tangent, t)
Line 886: Line 887:
## dB = derivative(binormal(t), t) ## dB = derivative(binormal, t)
Line 907: Line 908:
    pos_tzero = position(t0)     pos_tzero = position(t=t0)
Line 911: Line 912:
    speed_component = speed(t0)
    tangent_component = speed_deriv(t0)
    normal_component = sqrt( acceleration(t0).norm()^2 - tangent_component^2 )		     speed_component = speed(t=t0)
    tangent_component = speed_deriv(t=t0)
    normal_component = sqrt( acceleration(t=t0).norm()^2 - tangent_component^2 )
Line 920: Line 921:
    tan = arrow3d(pos_tzero, pos_tzero + tangent(t0), rgbcolor=(0,1,0) )
    vel = arrow3d(pos_tzero, pos_tzero + velocity(t0), rgbcolor=(0,0.5,0))
    nor = arrow3d(pos_tzero, pos_tzero + normal(t0), rgbcolor=(0.5,0,0))
    bin = arrow3d(pos_tzero, pos_tzero + binormal(t0), rgbcolor=(0,0,0.5))
    acc = arrow3d(pos_tzero, pos_tzero + acceleration(t0), rgbcolor=(1,0,1))
    tancomp = arrow3d(pos_tzero, pos_tzero + tangent_component*tangent(t0), rgbcolor=(1,0,1) )
    norcomp = arrow3d(pos_tzero, pos_tzero + normal_component*normal(t0), rgbcolor=(1,0,1))		     tan = arrow3d(pos_tzero, pos_tzero + tangent(t=t0), rgbcolor=(0,1,0) )
    vel = arrow3d(pos_tzero, pos_tzero + velocity(t=t0), rgbcolor=(0,0.5,0))
    nor = arrow3d(pos_tzero, pos_tzero + normal(t=t0), rgbcolor=(0.5,0,0))
    bin = arrow3d(pos_tzero, pos_tzero + binormal(t=t0), rgbcolor=(0,0,0.5))
    acc = arrow3d(pos_tzero, pos_tzero + acceleration(t=t0), rgbcolor=(1,0,1))
    tancomp = arrow3d(pos_tzero, pos_tzero + tangent_component*tangent(t=t0), rgbcolor=(1,0,1) )
    norcomp = arrow3d(pos_tzero, pos_tzero + normal_component*normal(t=t0), rgbcolor=(1,0,1))
Line 950: Line 951:
    print "Position vector: r(t)=", position(t)
    print "Speed is ", N(speed(t0))
    print "Curvature is ", N(curvature)
    ## print "Torsion is ", N(torsion)
    print
    print "Right-click on graphic to zoom to 400%"
    print "Drag graphic to rotate"		     print("Position vector: r(t)=", position)
    print("Speed is ", N(speed(t=t0)))
    print("Curvature is ", N(curvature))
    ## print("Torsion is ", N(torsion))
    print()
    print("Right-click on graphic to zoom to 400%")
    print("Drag graphic to rotate")
Line 1032: Line 1033:
        pretty_print(html('\n<center><font color="red">$\lim_{(x,?)\\rightarrow(x_0,y_0)} f(x,y) =%s$</font>'%str(limit_x)+' and <font color="red">$\lim_{(?,y)\\rightarrow(x_0,y_0)} f(x,y) =%s$</font></center>'%str(limit_y)))         pretty_print(html(r'<center><font color="red">$\lim_{(x,?)\rightarrow(x_0,y_0)} f(x,y) =%s$</font>'%str(limit_x)+r' and <font color="red">$\lim_{(?,y)\rightarrow(x_0,y_0)} f(x,y) =%s$</font></center>'%str(limit_y)))
Line 1043: Line 1044:
Line 1069: Line 1069:
    pretty_print(html('Enter $(x_0 ,y_0 )$ above and see what happens as the number of contour levels $\\rightarrow \infty $.'))     pretty_print(html(r'Enter $(x_0 ,y_0 )$ above and see what happens as the number of contour levels $\rightarrow \infty $.'))
Line 1082: Line 1082:
    pretty_print(table([[surface],['hi']]))     show(surface)
Line 1251: Line 1251:
      order=(1..10)):       order=[1..10]):
Line 1383: Line 1383:
== Lateral Surface Area (FIXME in Jupyter) == == Lateral Surface Area ==
Line 1388: Line 1388:

Note that this works in Sage cell, but causes a zip file error in Jupyter
Line 1455: Line 1457:
== Parametric surface example (FIXME in Jupyter) == == Parametric surface example ==
Line 1457: Line 1459:

Note that this works in Sage cell, but causes a zip file error in Jupyter.
Line 1505: Line 1509:
    u(t) = u
    v(t) = v
    w(t) = w

Sage Interactions - Calculus

goto interact main page

Contents

  1. Sage Interactions - Calculus
    1. Root Finding Using Bisection
    2. Newton's Method
    3. A contour map and 3d plot of two inverse distance functions
    4. A simple tangent line grapher
    5. Numerical integrals with the midpoint rule
    6. Numerical integrals with various rules
    7. Some polar parametric curves
    8. Function tool
    9. Newton-Raphson Root Finding
    10. Coordinate Transformations
    11. Taylor Series
    12. Illustration of the precise definition of a limit
    13. A graphical illustration of sin(x)/x -> 1 as x-> 0
    14. Quadric Surface Plotter
    15. The midpoint rule for numerically integrating a function of two variables
    16. Gaussian (Legendre) quadrature
    17. Vector Calculus, 2-D Motion
    18. Vector Calculus, 3-D Motion
    19. Multivariate Limits by Definition
    20. Directional Derivatives
    21. 3D graph with points and curves
    22. Approximating function in two variables by differential
    23. Taylor approximations in two variables
    24. Volumes over non-rectangular domains
    25. Lateral Surface Area
    26. Parametric surface example
    27. Line Integrals in 3D Vector Field

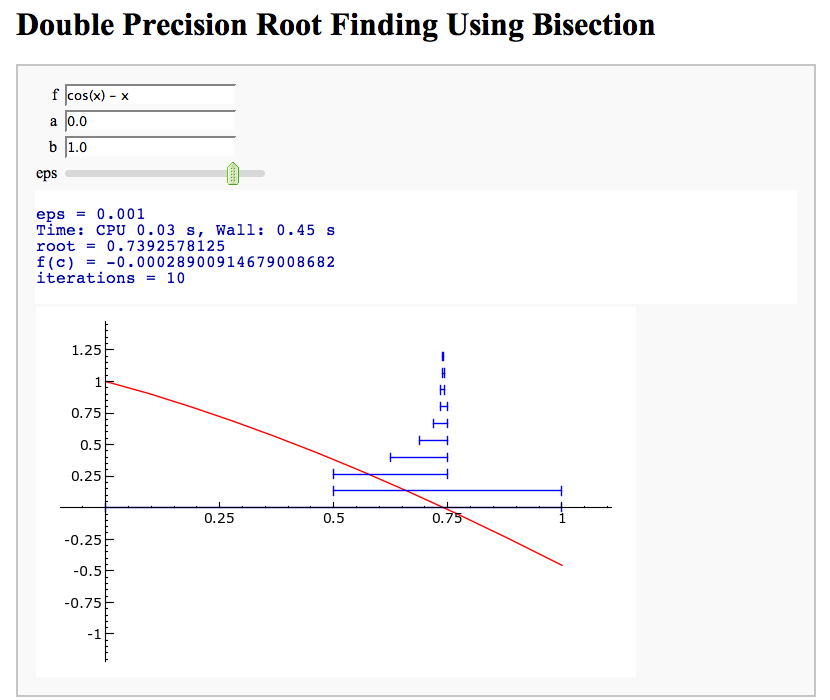
Root Finding Using Bisection

by William Stein

bisect.png

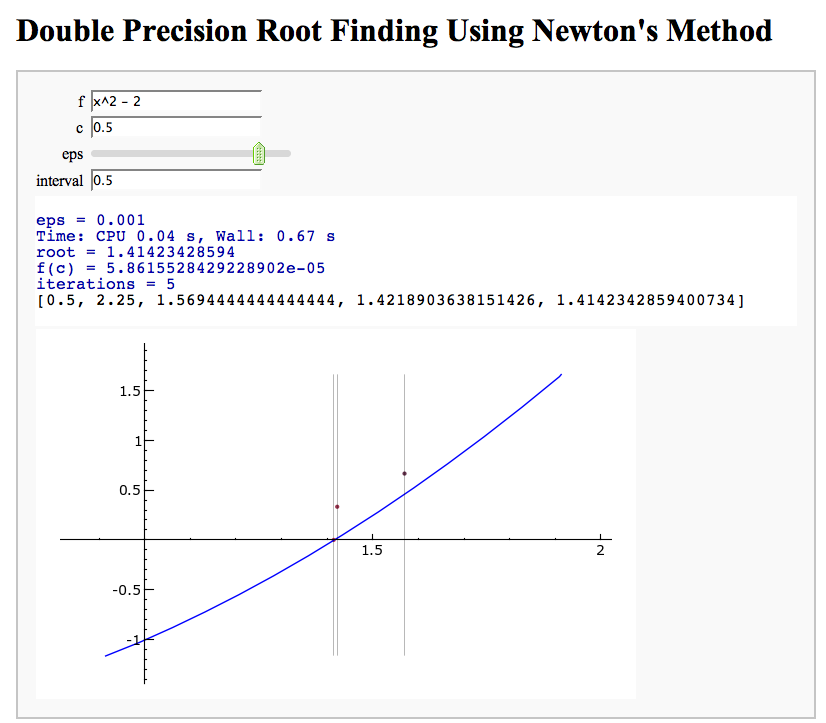
Newton's Method

Note that there is a more complicated Newton's method below.

by William Stein

https://cloud.sagemath.com/projects/19575ea0-317e-402b-be57-368d04c113db/files/pub/2801-2901/2824-Double%20Precision%20Root%20Finding%20Using%20Newton's%20Method.sagews

newton.png

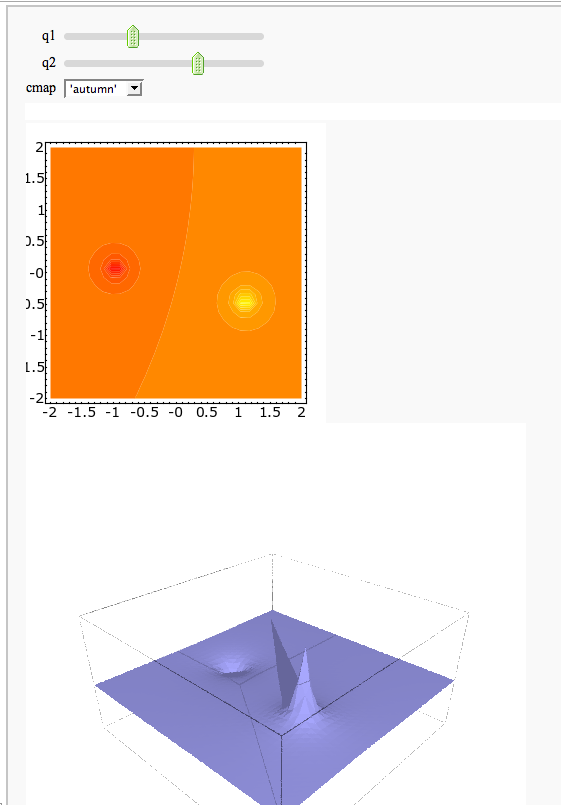
A contour map and 3d plot of two inverse distance functions

by William Stein

https://cloud.sagemath.com/projects/19575ea0-317e-402b-be57-368d04c113db/files/pub/2801-2901/2823.sagews

mountains.png

A simple tangent line grapher

by Marshall Hampton

tangents.png

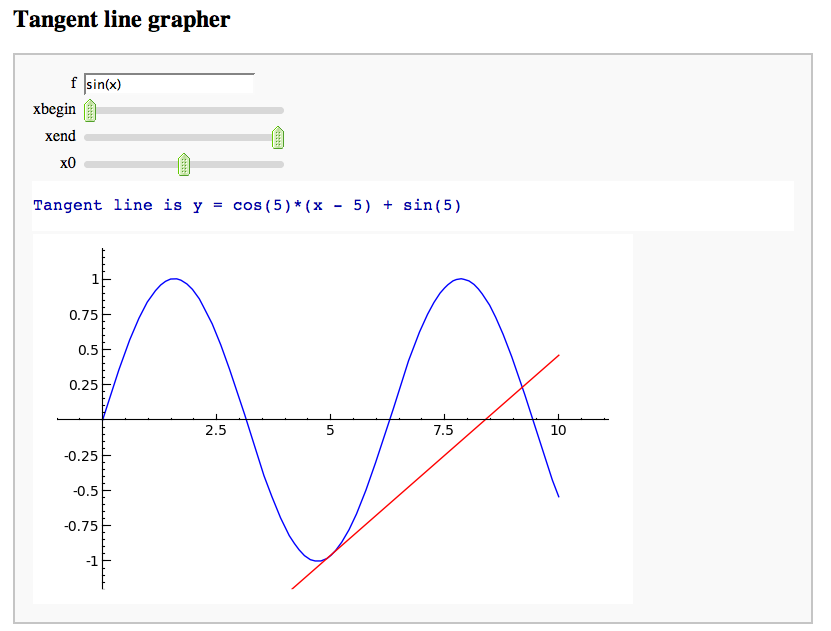
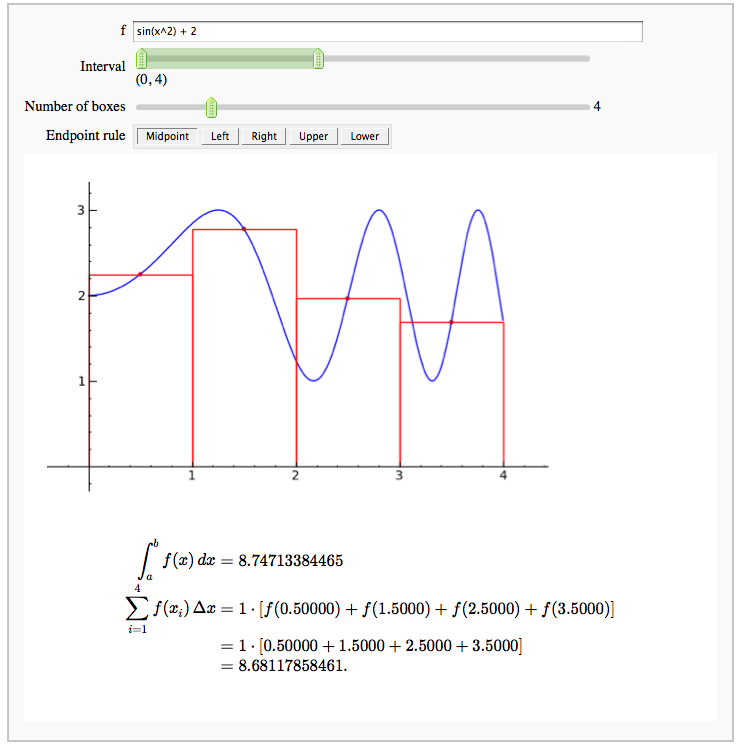
Numerical integrals with the midpoint rule

by Marshall Hampton

num_int.png

Numerical integrals with various rules

by Nick Alexander (based on the work of Marshall Hampton)

num_int2.png

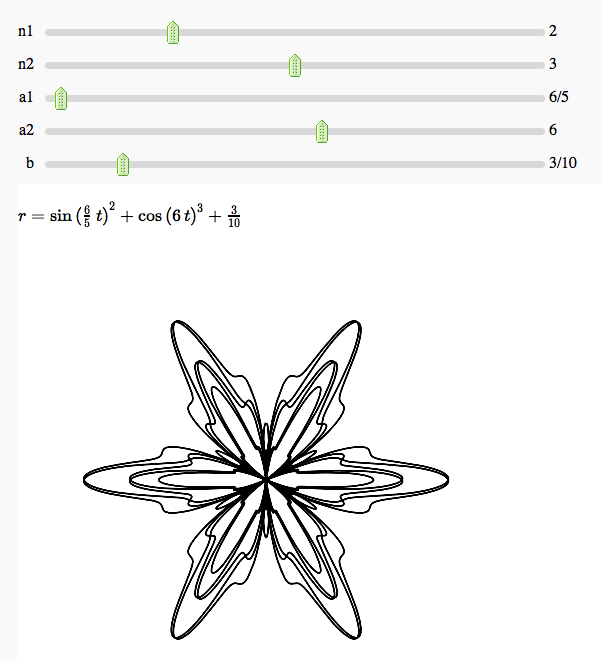
Some polar parametric curves

by Marshall Hampton. This is not very general, but could be modified to show other families of polar curves.

polarcurves1.png

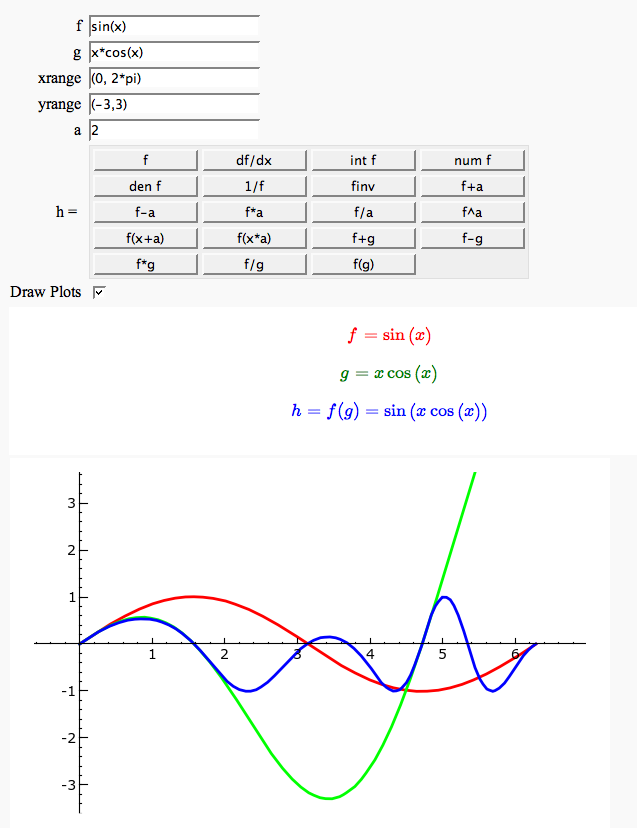
Function tool

Enter symbolic functions f, g, and a, a range, then click the appropriate button to compute and plot some combination of f, g, and a along with f and g. This is inspired by the Matlab funtool GUI.

funtool.png

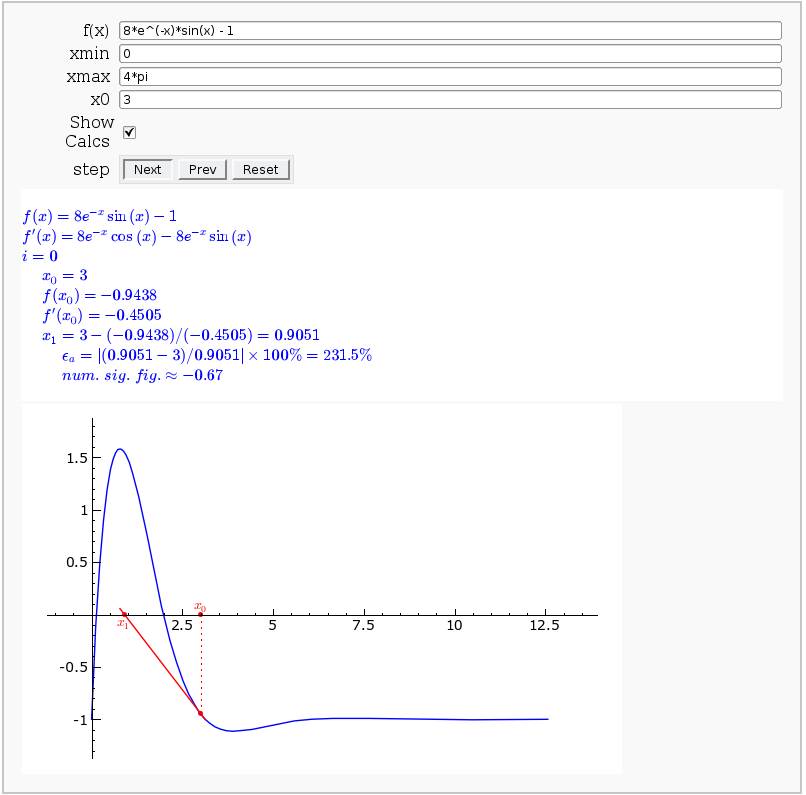
Newton-Raphson Root Finding

by Neal Holtz

This allows user to display the Newton-Raphson procedure one step at a time. It uses the heuristic that, if any of the values of the controls change, then the procedure should be re-started, else it should be continued.

newtraph.png

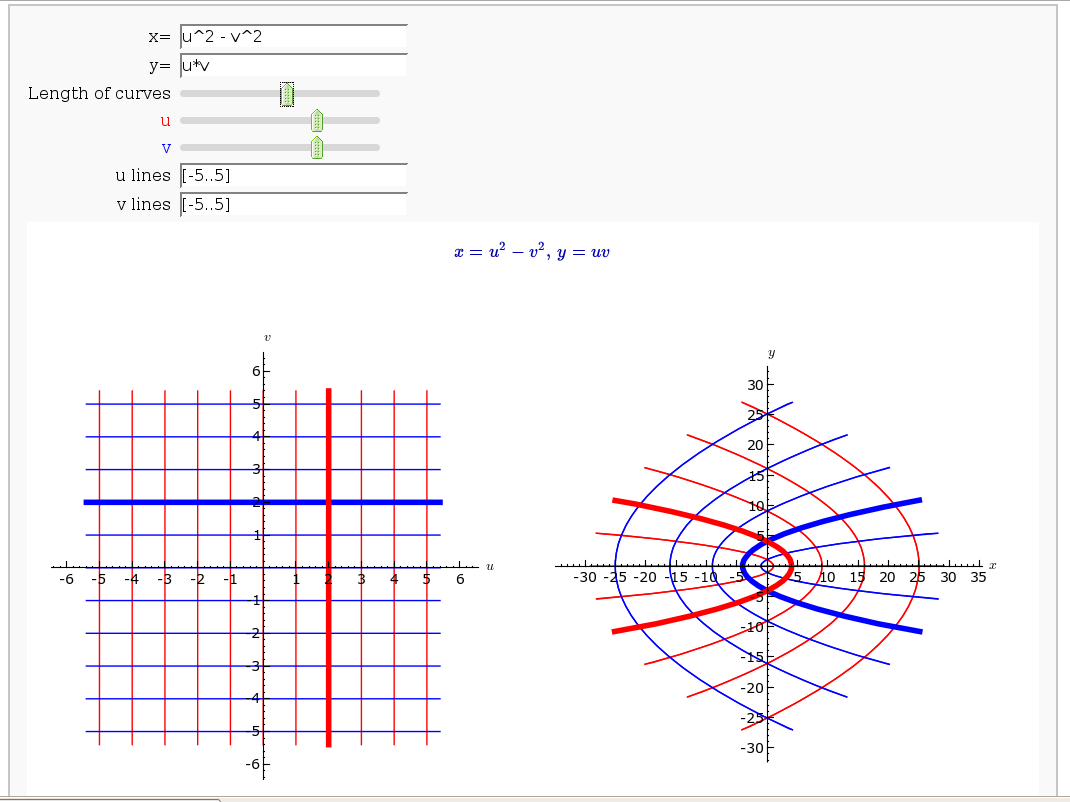
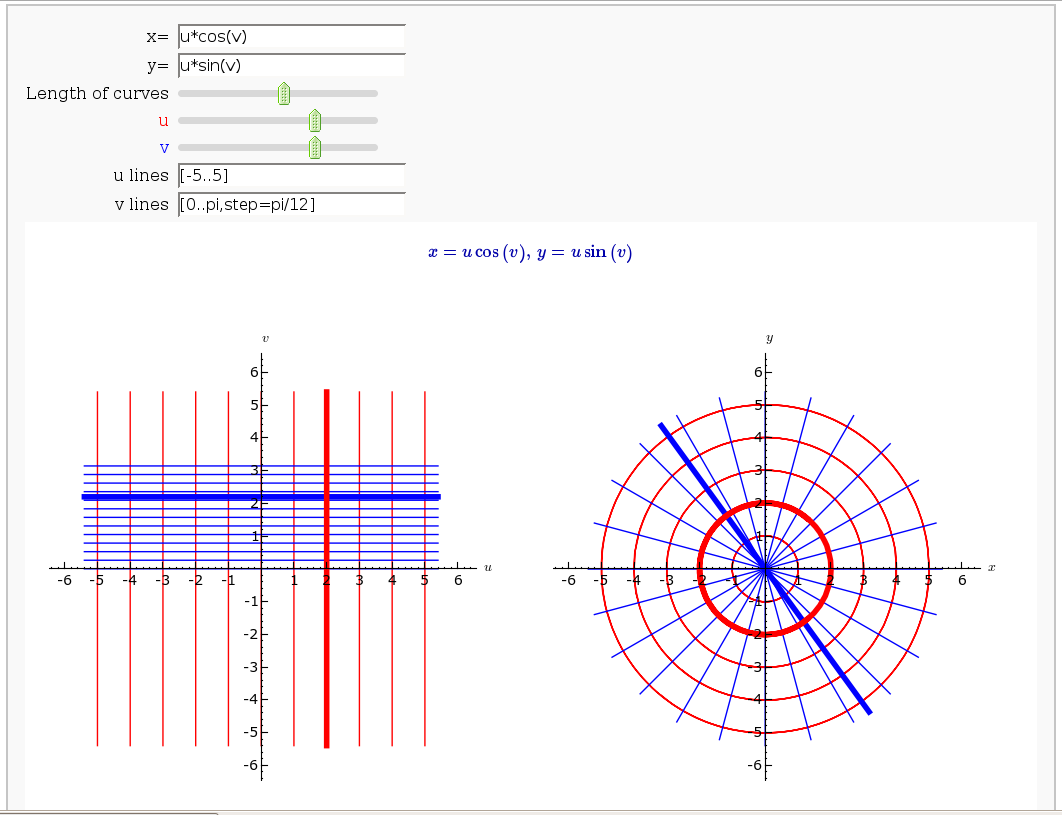
Coordinate Transformations

by Jason Grout

coordinate-transform-1.png coordinate-transform-2.png

Taylor Series

by Harald Schilly

taylor_series_animated.gif

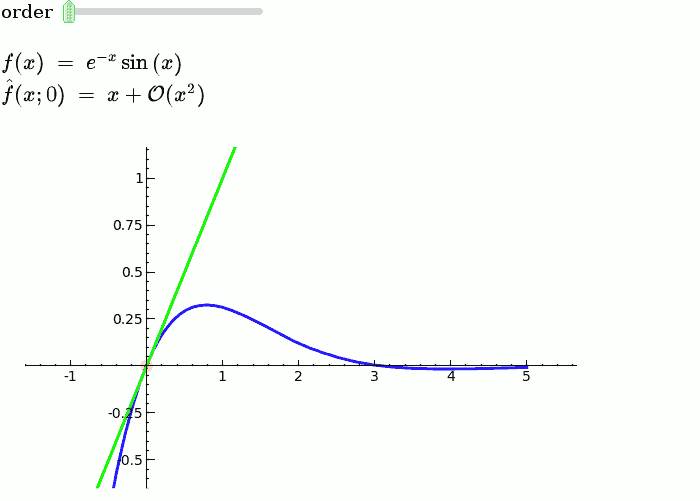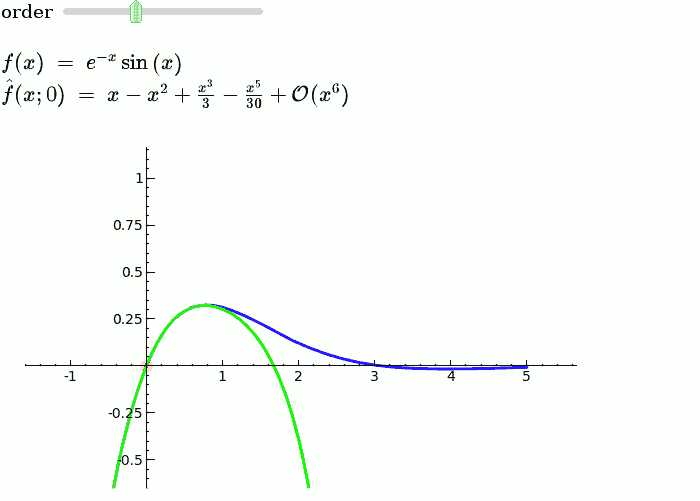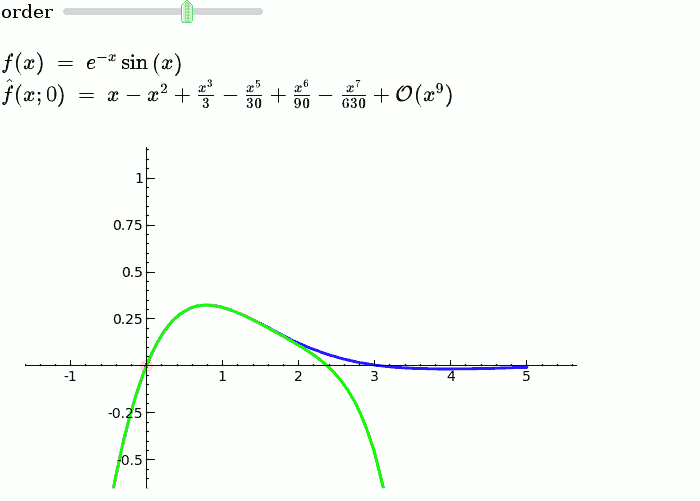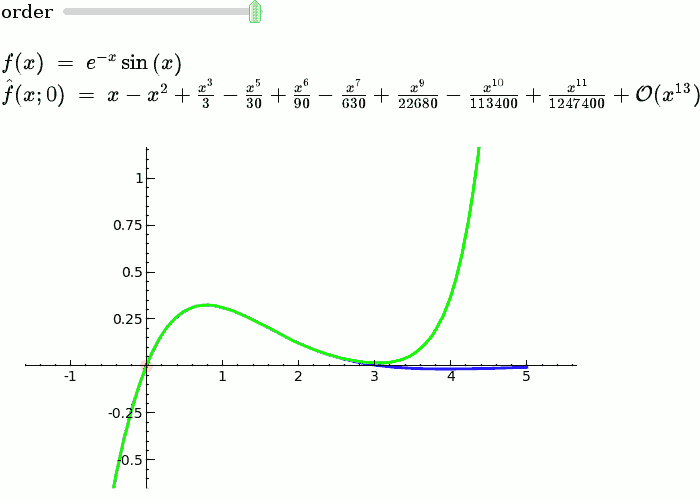
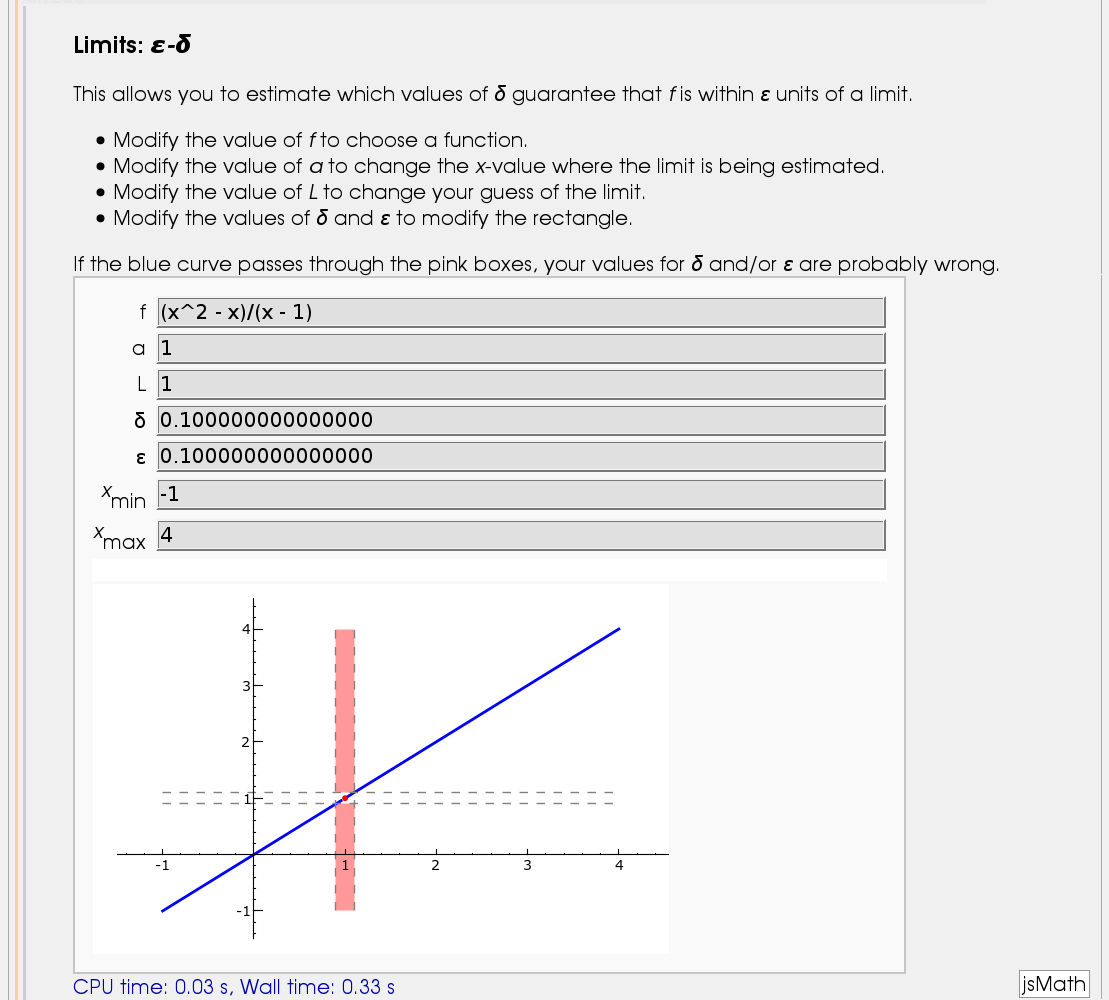
Illustration of the precise definition of a limit

by John Perry

I'll break tradition and put the image first. Apologies if this is Not A Good Thing.

snapshot_epsilon_delta.png

A graphical illustration of sin(x)/x -> 1 as x-> 0

by Wai Yan Pong

sinelimit.png

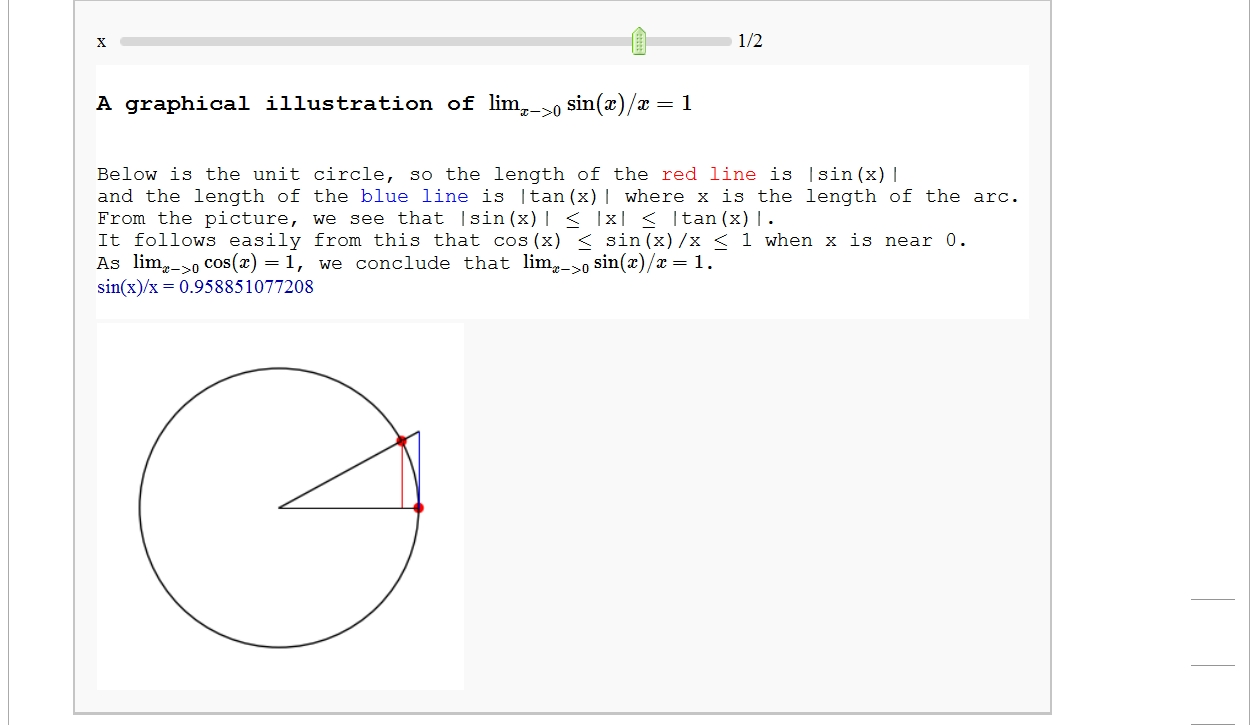
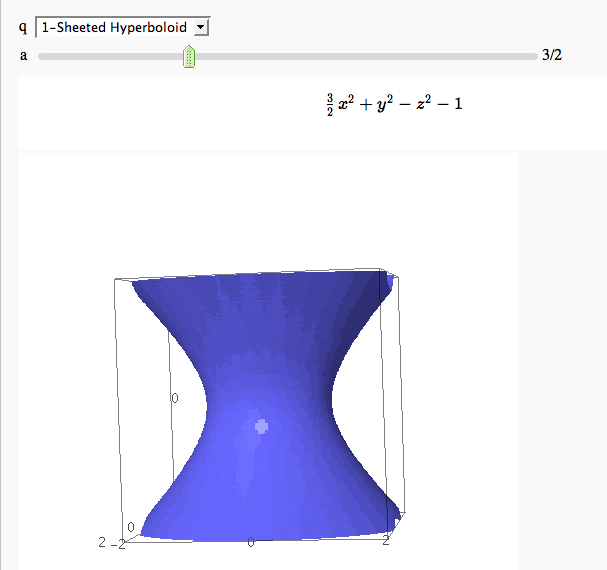
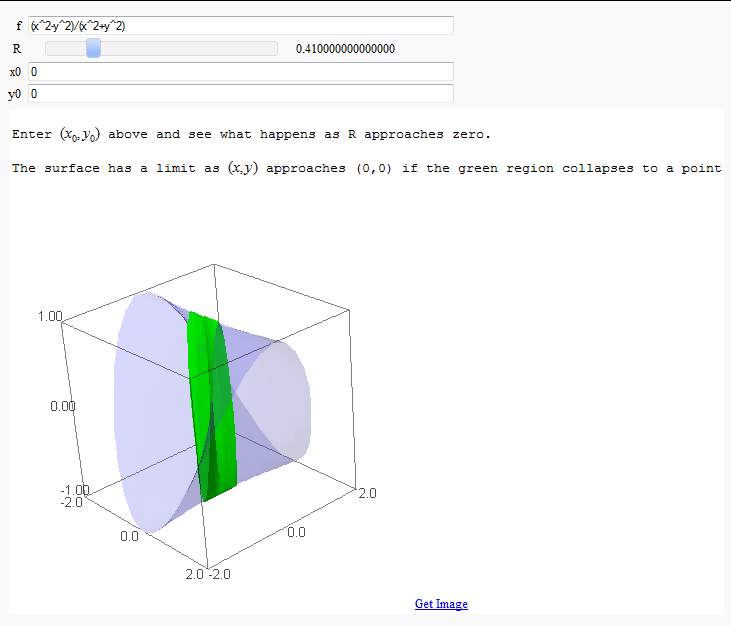
Quadric Surface Plotter

by Marshall Hampton. This is pretty simple, so I encourage people to spruce it up. In particular, it isn't set up to show all possible types of quadrics.

quadrics.png

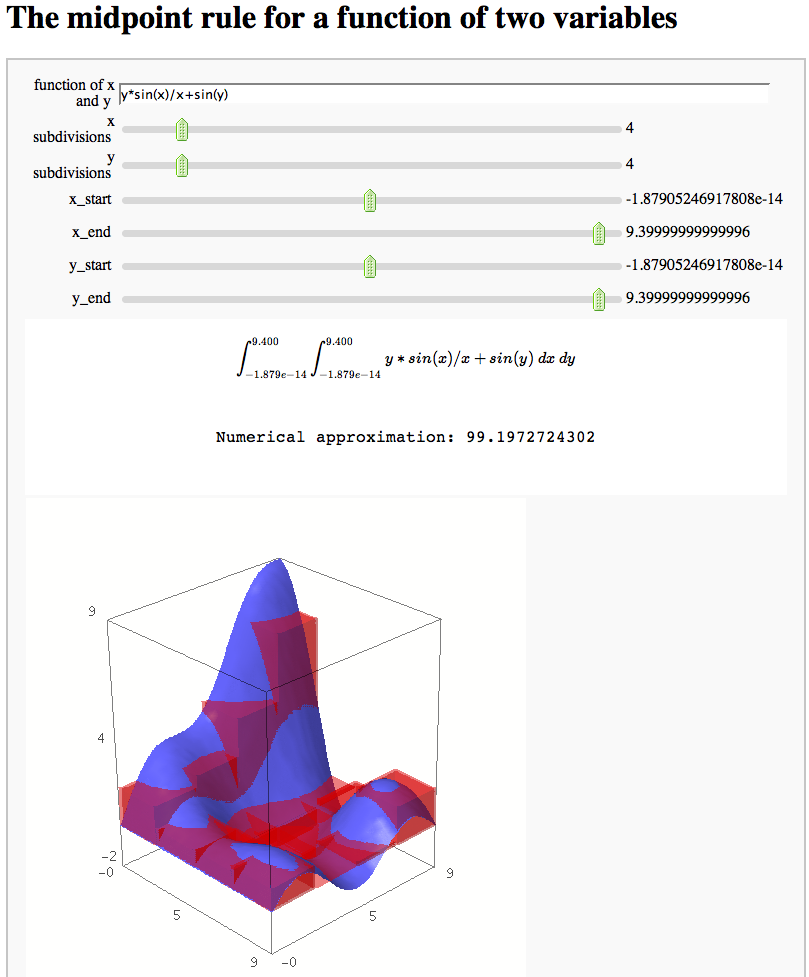
The midpoint rule for numerically integrating a function of two variables

by Marshall Hampton

numint2d.png

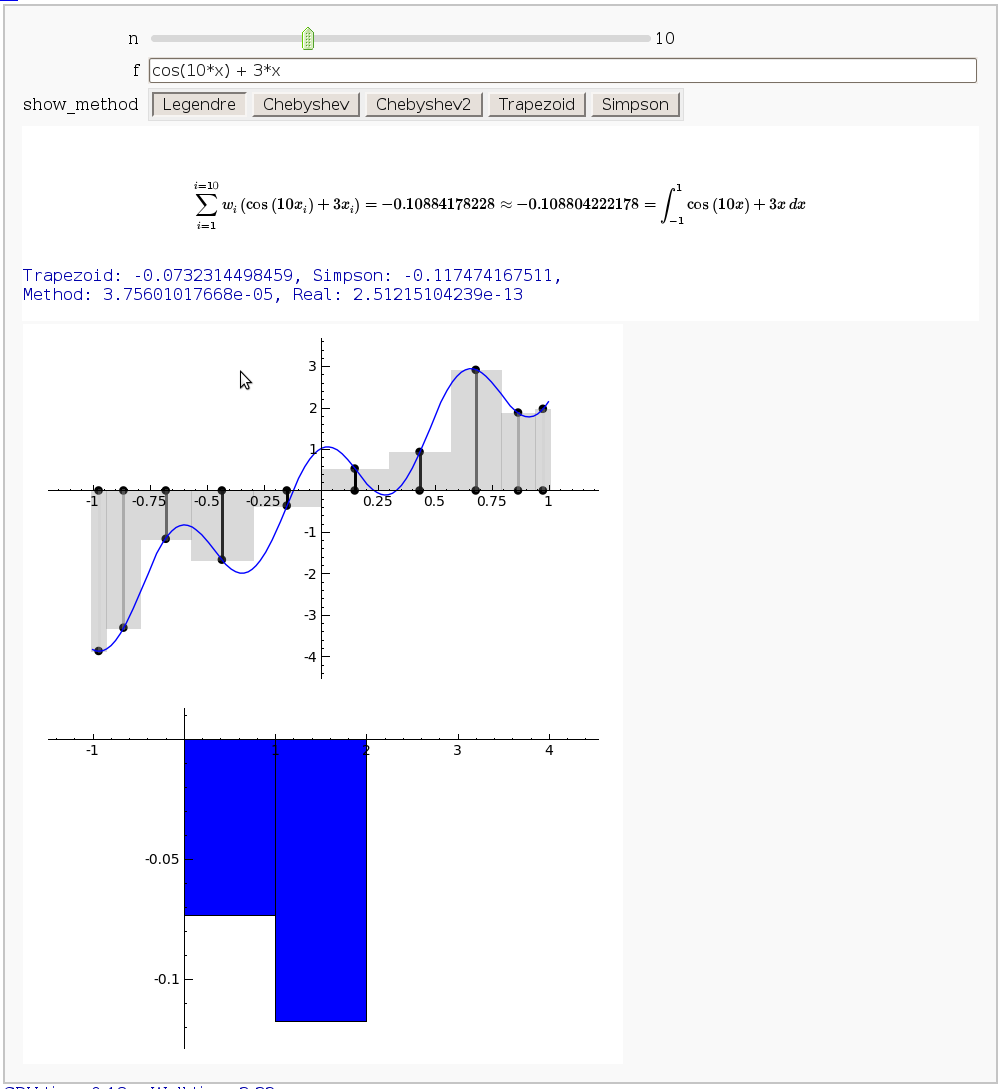
Gaussian (Legendre) quadrature

by Jason Grout

The output shows the points evaluated using Gaussian quadrature (using a weight of 1, so using Legendre polynomials). The vertical bars are shaded to represent the relative weights of the points (darker = more weight). The error in the trapezoid, Simpson, and quadrature methods is both printed out and compared through a bar graph. The "Real" error is the error returned from scipy on the definite integral.

quadrature1.png quadrature2.png

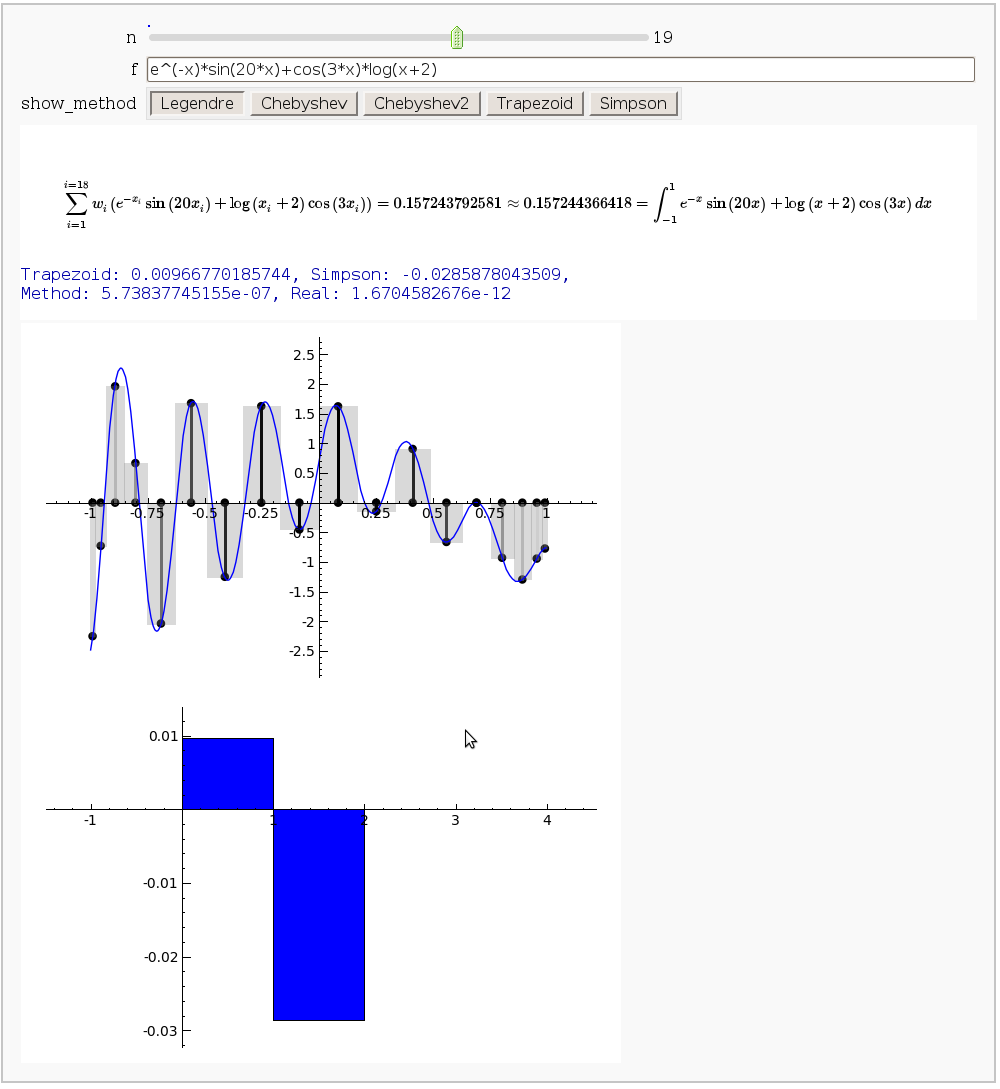
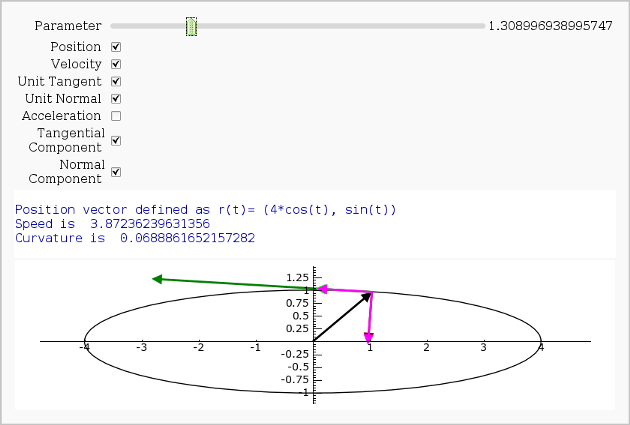
Vector Calculus, 2-D Motion

By Rob Beezer

A fast_float() version is available in a worksheet

motion2d.png

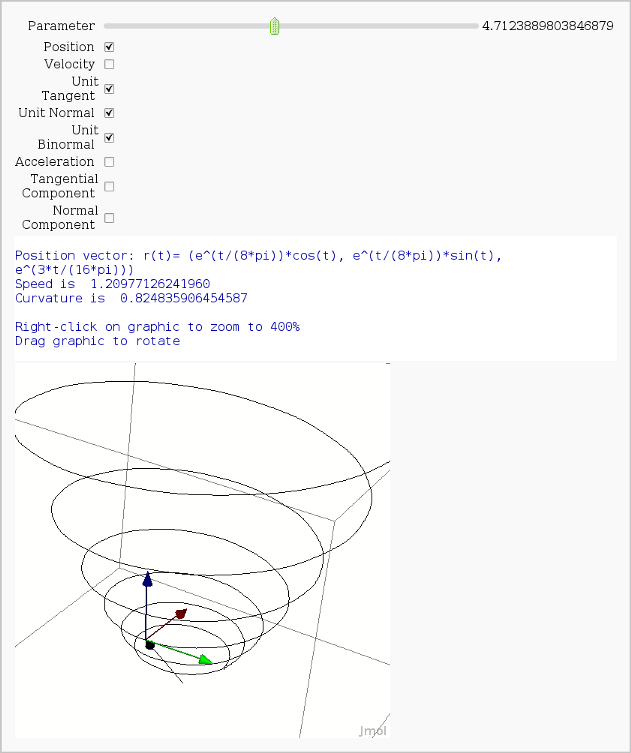
Vector Calculus, 3-D Motion

by Rob Beezer

Available as a worksheet

motion3d.png

Multivariate Limits by Definition

by John Travis

http://sagenb.mc.edu/home/pub/97/

3D_Limit_Defn.png

3D_Limit_Defn_Contours.png

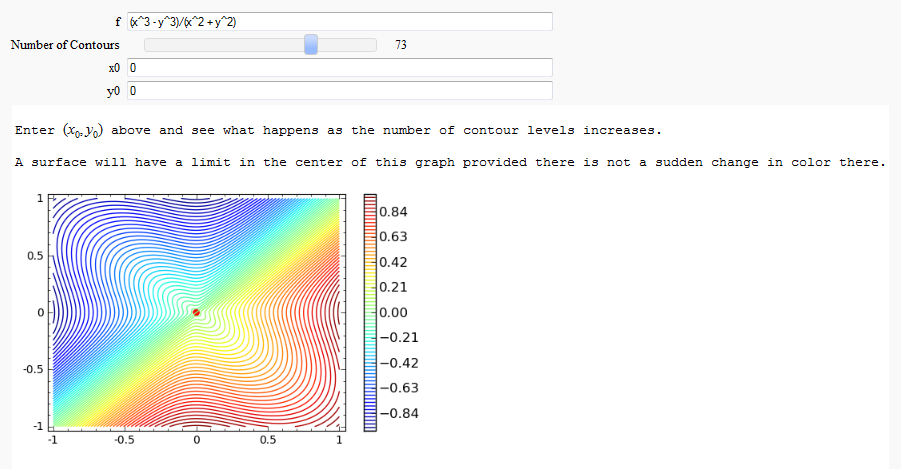
Directional Derivatives

This interact displays graphically a tangent line to a function, illustrating a directional derivative (the slope of the tangent line).

directional derivative.png

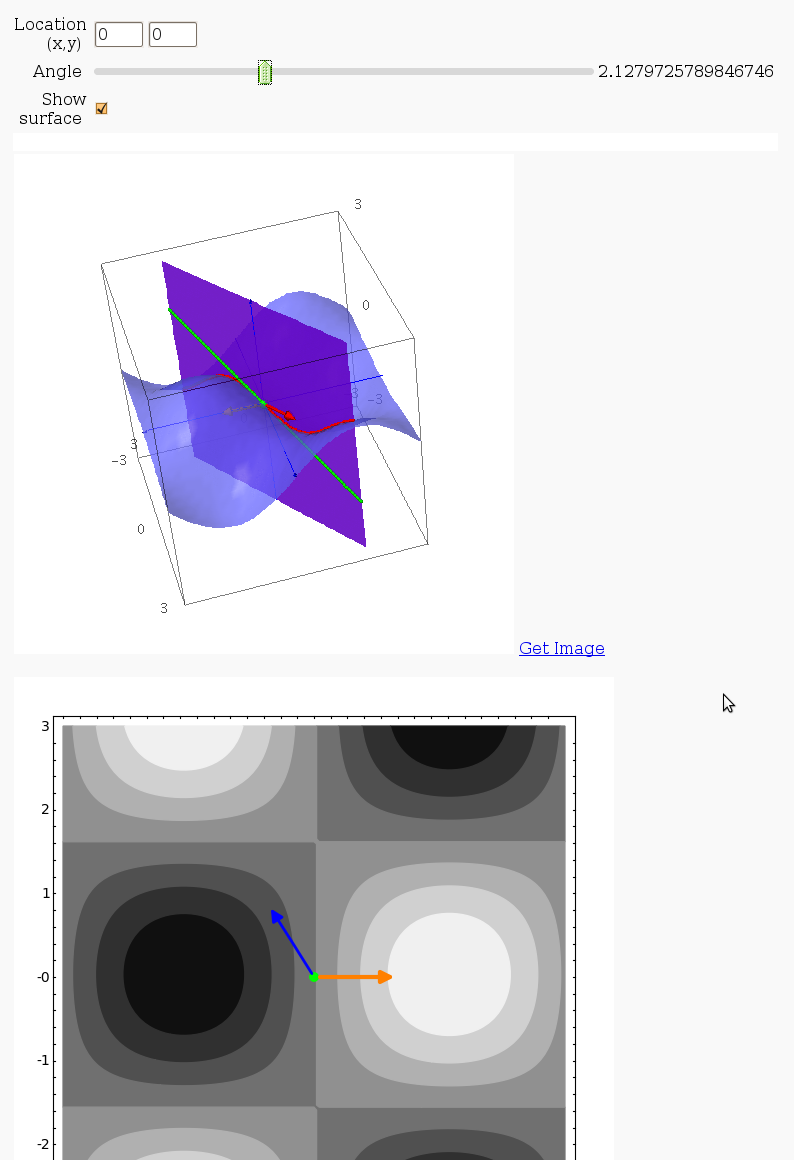
3D graph with points and curves

By Robert Marik

This sagelet is handy when showing local, constrained and absolute maxima and minima in two variables. Available as a worksheet

3Dgraph_with_points.png

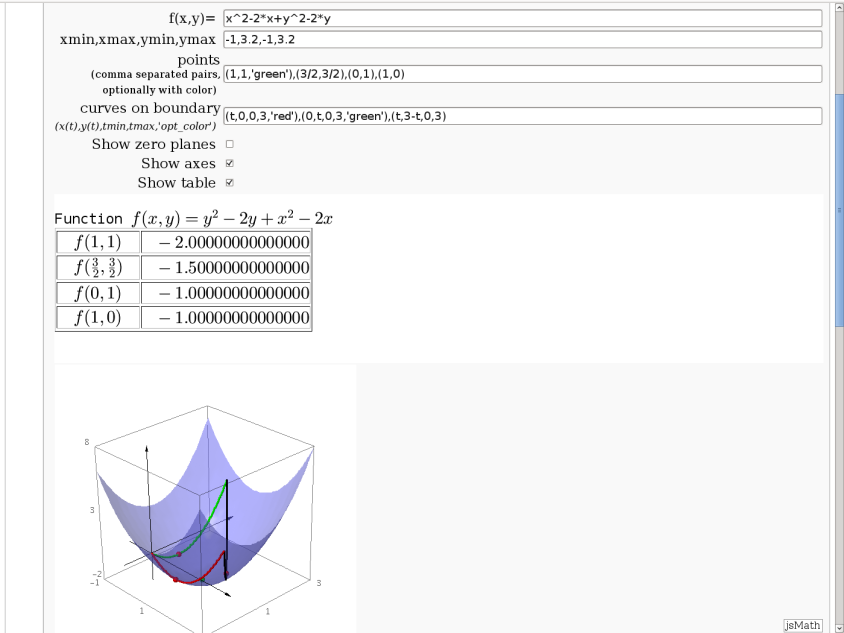
Approximating function in two variables by differential

by Robert Marik

3D_differential.png

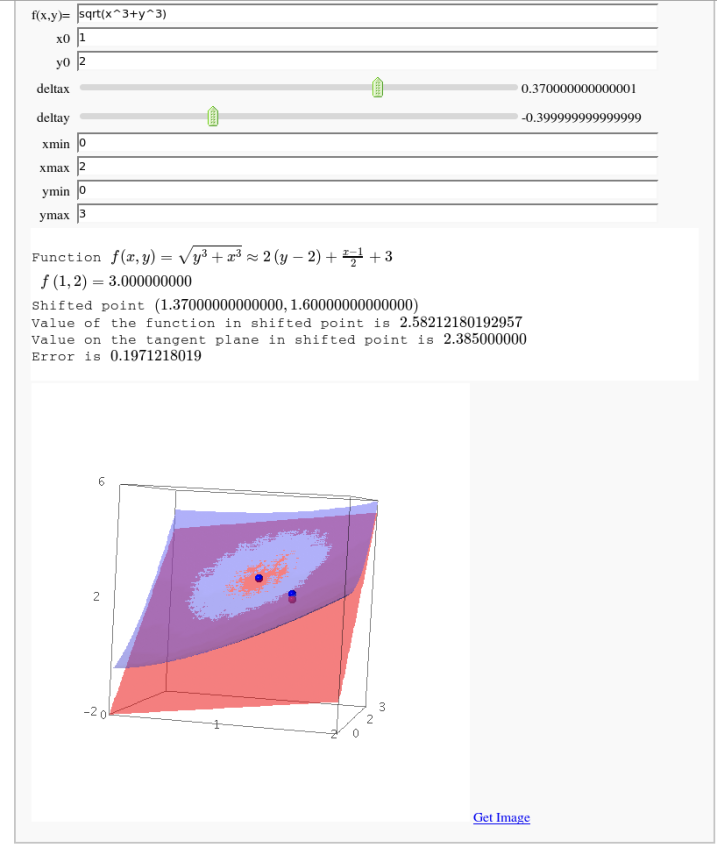
Taylor approximations in two variables

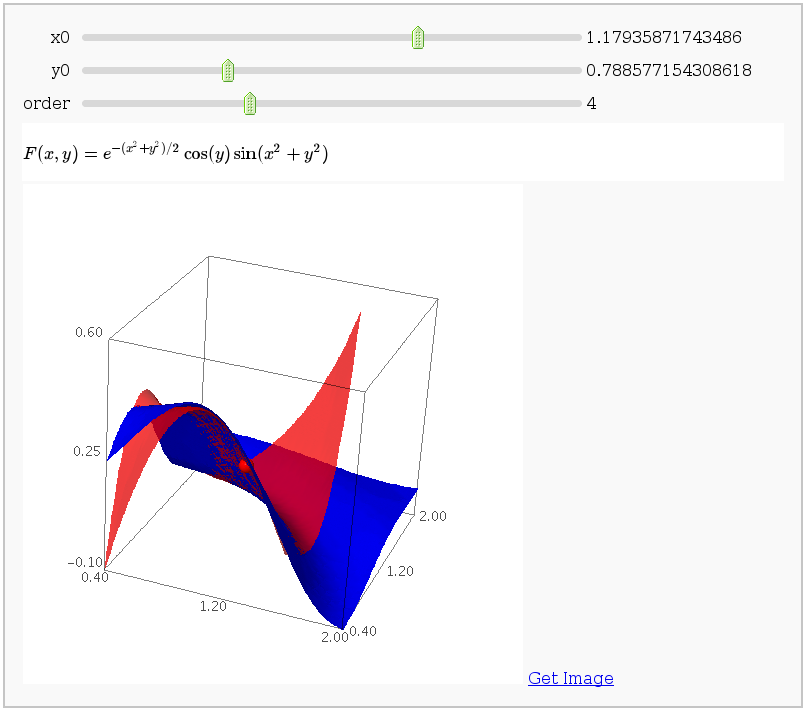
by John Palmieri

This displays the nth order Taylor approximation, for n from 1 to 10, of the function sin(x2 + y2) cos(y) exp(-(x2+y2)/2).

taylor-3d.png

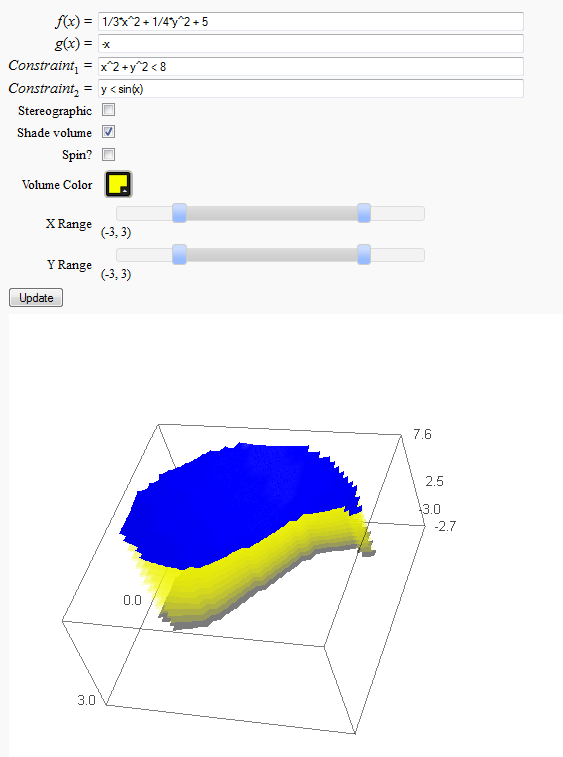
Volumes over non-rectangular domains

by John Travis

https://cloud.sagemath.com/projects/19575ea0-317e-402b-be57-368d04c113db/files/pub/2801-2901/2829.sagews

3D_Irregular_Volume.png

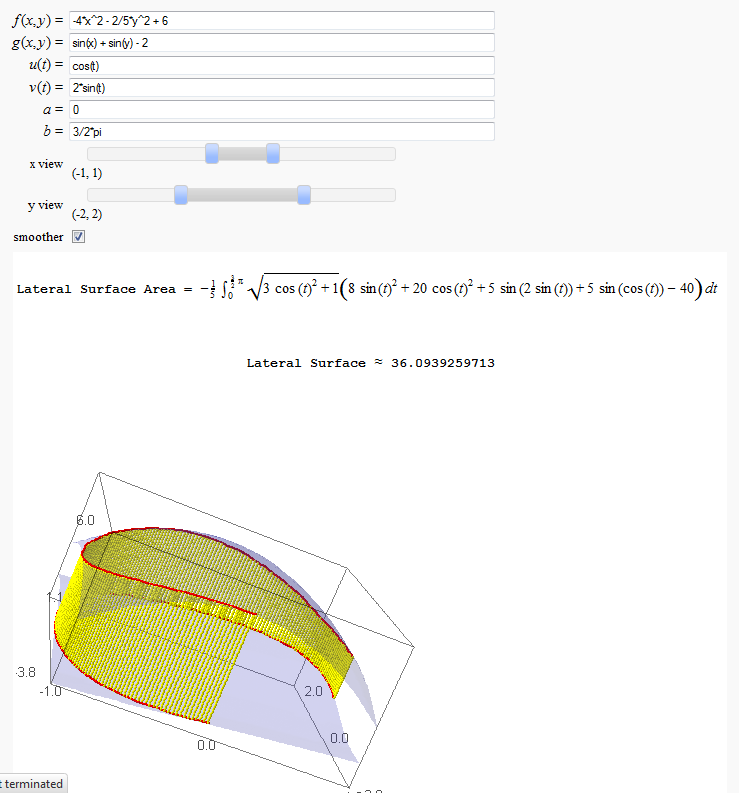
Lateral Surface Area

by John Travis

http://sagenb.mc.edu/home/pub/89/

Note that this works in Sage cell, but causes a zip file error in Jupyter

Lateral_Surface.png

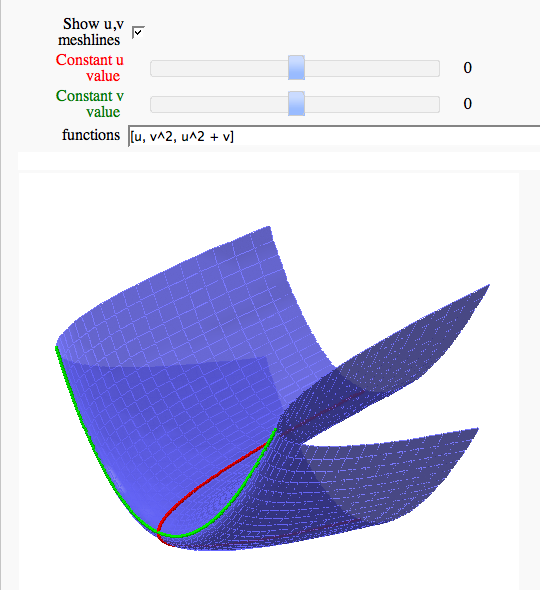
Parametric surface example

by Marshall Hampton

Note that this works in Sage cell, but causes a zip file error in Jupyter.

parametric_surface.png

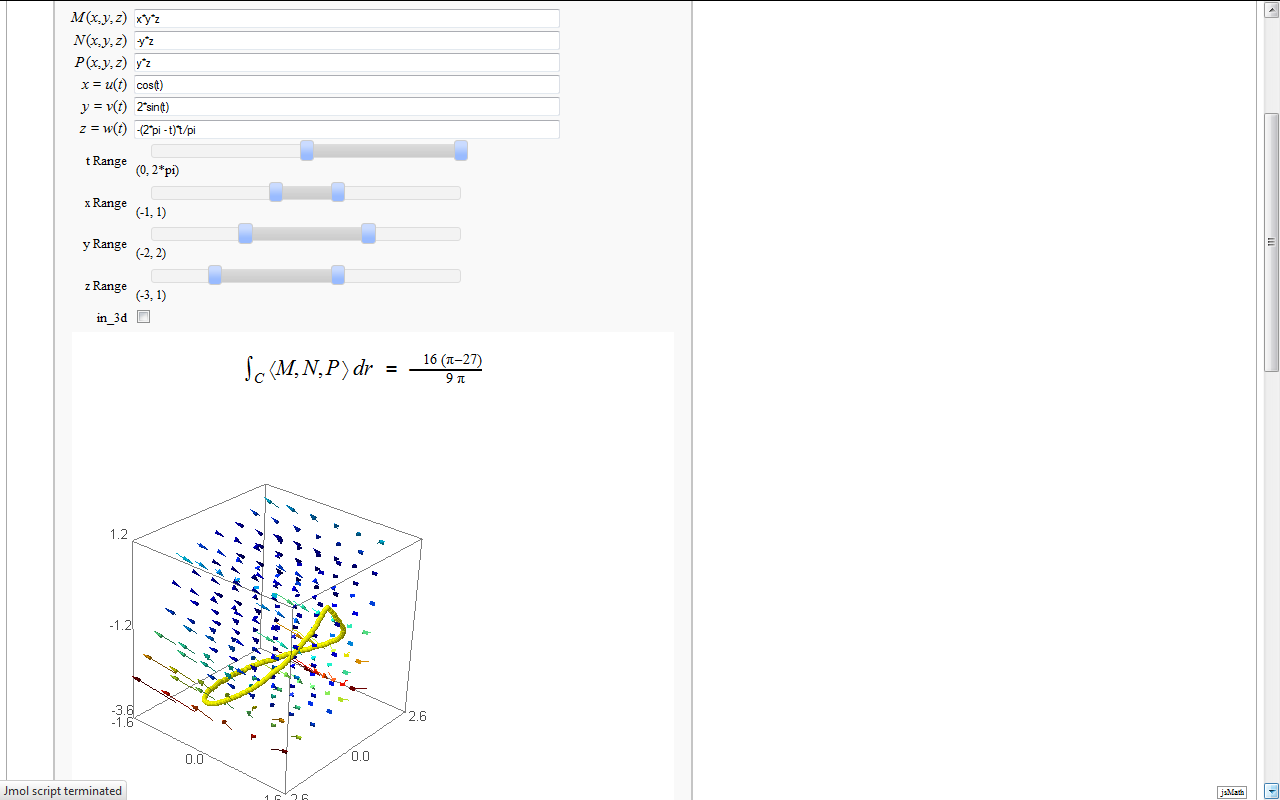
Line Integrals in 3D Vector Field

by John Travis

https://cloud.sagemath.com/projects/19575ea0-317e-402b-be57-368d04c113db/files/pub/2801-2901/2827-$%20%5Cint_%7BC%7D%20%5Cleft%20%5Clangle%20M,N,P%20%5Cright%20%5Crangle%20dr%20$%20=%20$%20%25s%20$.sagews

3D_Line_Integral.png

interact/calculus (last edited 2020-08-11 14:10:09 by kcrisman)