Differences between revisions 11 and 27 (spanning 16 versions)
⇤ ← Revision 11 as of 2009-02-06 04:19:02 →
Size: 30130
Editor: TimothyClemans
Comment:
← Revision 27 as of 2012-05-09 12:58:01 → ⇥
Size: 30437
Editor: chapoton
Comment: removed j in Computing modular forms (fixed)
Deletions are marked like this. Additions are marked like this.
Line 4: Line 4:

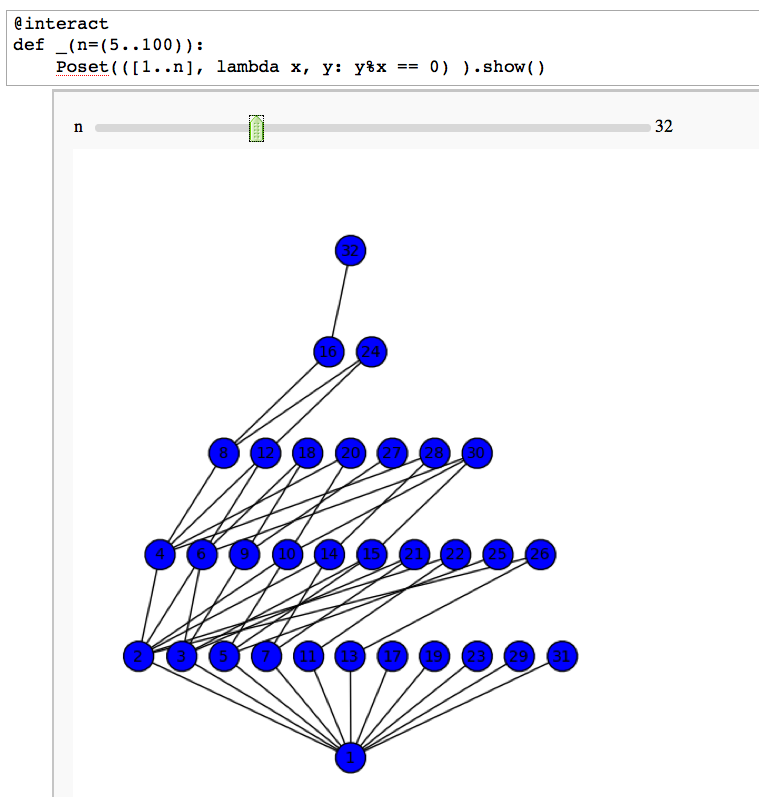
== Divisibility Poset ==
by William Stein
{{{#!sagecell
@interact
def _(n=(5..100)):
    Poset(([1..n], lambda x, y: y%x == 0) ).show()
}}}

{{attachment:divposet.png}}
Line 7: Line 18:
{{{ {{{#!sagecell
Line 61: Line 72:
{{{ {{{#!sagecell
Line 75: Line 86:
{{{ {{{#!sagecell
Line 83: Line 94:
== Prime Spiral - Square == == Prime Spiral - Square FIXME ==
Line 85: Line 96:
{{{ {{{#!sagecell
Line 134: Line 145:
        N = M.copy()         N = copy(M)
Line 222: Line 233:
{{{ {{{#!sagecell
Line 296: Line 307:
{{{
j = 0		 {{{#!sagecell
Line 302: Line 312:
    print j; global j; j += 1
Line 319: Line 328:
{{{ {{{#!sagecell
Line 329: Line 338:
== A Charpoly and Hecke Operator Graph == == A Charpoly and Hecke Operator Graph FIXME ==
Line 332: Line 341:
{{{ {{{#!sagecell
Line 353: Line 362:
== Quadratic Residue Table == == Quadratic Residue Table FIXME ==
Line 355: Line 364:
{{{ {{{#!sagecell
Line 406: Line 415:
== Cubic Residue Table == == Cubic Residue Table FIXME ==
Line 408: Line 417:
{{{ {{{#!sagecell
Line 426: Line 435:
    if Mod(a,3)!=0 and Mod(b,3)==0:
        return True
    else:
        return False		     return Mod(a,3)!=0 and Mod(b,3)==0
Line 492: Line 498:
{{{ {{{#!sagecell
Line 541: Line 547:
    S = circle((0,0),1,rgbcolor='yellow')  \
    + line([e_pt,e_gs_pt], rgbcolor='red', thickness=4) \
    + line([f_pt,f_gs_pt], rgbcolor='blue', thickness=3) \
    + line([ef_pt,ef_gs_pt], rgbcolor='purple',thickness=2) \
    + point(e_pt,pointsize=50, rgbcolor='red')  \
    + point(f_pt,pointsize=50, rgbcolor='blue') \
    + point(ef_pt,pointsize=50,rgbcolor='purple') \
    + point(f_gs_pt,pointsize=75, rgbcolor='black') \
    + point(e_gs_pt,pointsize=75, rgbcolor='black') \
    + point(ef_gs_pt,pointsize=75, rgbcolor='black') \
    + point(js_pt,pointsize=100,rgbcolor='green')		     S = circle((0,0),1,rgbcolor='yellow')
    S += line([e_pt,e_gs_pt], rgbcolor='red', thickness=4)
    S += line([f_pt,f_gs_pt], rgbcolor='blue', thickness=3)
    S += line([ef_pt,ef_gs_pt], rgbcolor='purple',thickness=2)
    S += point(e_pt,pointsize=50, rgbcolor='red')
    S += point(f_pt,pointsize=50, rgbcolor='blue')
    S += point(ef_pt,pointsize=50,rgbcolor='purple')
    S += point(f_gs_pt,pointsize=75, rgbcolor='black')             S += point(e_gs_pt,pointsize=75, rgbcolor='black')
    S += point(ef_gs_pt,pointsize=75, rgbcolor='black')
    S += point(js_pt,pointsize=100,rgbcolor='green')
Line 553: Line 559:
        S += text('$J(%s,%s) = %s$'%(latex2(e),latex2(f),latex(js)), \         S += text('$J(%s,%s) = %s$'%(latex2(e),latex2(f),latex(js)),
Line 572: Line 578:
{{{ {{{#!sagecell
Line 621: Line 627:
    S = circle((0,0),1,rgbcolor='yellow')  \
    + line([e_pt,e_gs_pt], rgbcolor='red', thickness=4) \
    + line([f_pt,f_gs_pt], rgbcolor='blue', thickness=3) \
    + line([ef_pt,ef_gs_pt], rgbcolor='purple',thickness=2) \
    + point(e_pt,pointsize=50, rgbcolor='red')  \
    + point(f_pt,pointsize=50, rgbcolor='blue') \
    + point(ef_pt,pointsize=50,rgbcolor='purple') \
    + point(f_gs_pt,pointsize=75, rgbcolor='black') \
    + point(e_gs_pt,pointsize=75, rgbcolor='black') \
    + point(ef_gs_pt,pointsize=75, rgbcolor='black') \
    + point(js_pt,pointsize=100,rgbcolor='green')		     S = circle((0,0),1,rgbcolor='yellow')
    S += line([e_pt,e_gs_pt], rgbcolor='red', thickness=4)
    S += line([f_pt,f_gs_pt], rgbcolor='blue', thickness=3)
    S += line([ef_pt,ef_gs_pt], rgbcolor='purple',thickness=2)
    S += point(e_pt,pointsize=50, rgbcolor='red')
    S += point(f_pt,pointsize=50, rgbcolor='blue')
    S += point(ef_pt,pointsize=50,rgbcolor='purple')
    S += point(f_gs_pt,pointsize=75, rgbcolor='black')
    S += point(e_gs_pt,pointsize=75, rgbcolor='black')
    S += point(ef_gs_pt,pointsize=75, rgbcolor='black')
    S += point(js_pt,pointsize=100,rgbcolor='green')
Line 633: Line 639:
        S += text('$J(%s,%s) = %s$'%(latex2(e),latex2(f),latex(js)), \         S += text('$J(%s,%s) = %s$'%(latex2(e),latex2(f),latex(js)),
Line 645: Line 651:
        ga[i].save('j%d.PNG'%i,figsize=4,aspect_ratio=1, \         ga[i].save('j%d.png'%i,figsize=4,aspect_ratio=1,
Line 651: Line 657:
    html('<table bgcolor=lightgrey cellpadding=2>')     s='<table bgcolor=lightgrey cellpadding=2>'
Line 653: Line 659:
        html('<tr><td align="center"><img src="cell://j%d.PNG"></td>'%(2*i))
        html('<td align="center"><img src="cell://j%d.PNG"></td></tr>'%(2*i+1))
    html('</table>')
}}}		         s+='<tr><td align="center"><img src="cell://j%d.png"></td>'%(2*i)
        s+='<td align="center"><img src="cell://j%d.png"></td></tr>'%(2*i+1)
    s+='</table>'
    html(s)}}}
Line 662: Line 668:
== Adding points on an elliptic curve == == Adding points on an elliptic curve FIXME ==
Line 664: Line 670:
{{{ {{{#!sagecell
Line 740: Line 746:
{{{ {{{#!sagecell
Line 755: Line 761:
{{{ {{{#!sagecell
Line 769: Line 775:
    print """
<html>		     html("""
Line 794: Line 799:
</ol></html> </ol>
Line 796: Line 801:
       (g^ b)^a, g^a, b, p, (g^a)^b)        (g^ b)^a, g^a, b, p, (g^a)^b))
Line 804: Line 809:
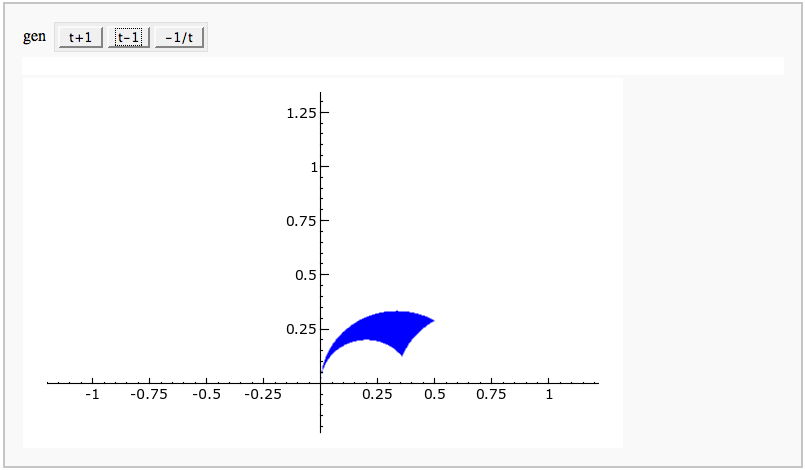
== Continued Fraction Plotter == == Continued Fraction Plotter FIXME ==
Line 806: Line 811:
{{{ {{{#!sagecell
Line 816: Line 821:
{{{ {{{#!sagecell
Line 837: Line 842:
{{{ {{{#!sagecell
Line 845: Line 850:
def _(gen = selector(['t+1', 't-1', '-1/t'], nrows=1)): def _(gen = selector(['t+1', 't-1', '-1/t'], buttons=True,nrows=1)):

Contents

  1. Integer Factorization
    1. Divisibility Poset
    2. Factor Trees
    3. Factoring an Integer
  2. Prime Numbers
    1. Illustrating the prime number theorem
    2. Prime Spiral - Square FIXME
    3. Prime Spiral - Polar
  3. Modular Forms
    1. Computing modular forms
    2. Computing the cuspidal subgroup
    3. A Charpoly and Hecke Operator Graph FIXME
  4. Modular Arithmetic
    1. Quadratic Residue Table FIXME
    2. Cubic Residue Table FIXME
  5. Cyclotomic Fields
    1. Gauss and Jacobi Sums in Complex Plane
    2. Exhaustive Jacobi Plotter
  6. Elliptic Curves
    1. Adding points on an elliptic curve FIXME
    2. Plotting an elliptic curve over a finite field
  7. Cryptography
    1. The Diffie-Hellman Key Exchange Protocol
  8. Other
    1. Continued Fraction Plotter FIXME
    2. Computing Generalized Bernoulli Numbers
    3. Fundamental Domains of SL_2(ZZ)

Integer Factorization

Divisibility Poset

by William Stein

divposet.png

Factor Trees

by William Stein

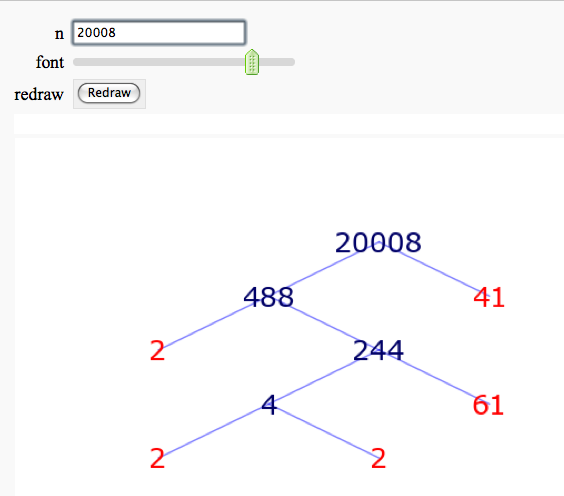
factortree.png

More complicated demonstration using Mathematica: http://demonstrations.wolfram.com/FactorTrees/

Factoring an Integer

by Timothy Clemans

Sage implementation of the Mathematica demonstration of the same name. http://demonstrations.wolfram.com/FactoringAnInteger/

Prime Numbers

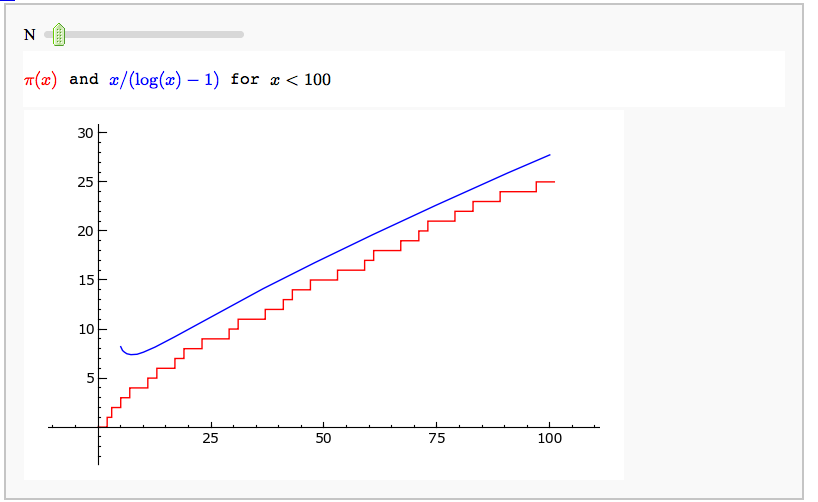
Illustrating the prime number theorem

by William Stein

primes.png

Prime Spiral - Square FIXME

by David Runde

SquareSpiral.PNG

Prime Spiral - Polar

by David Runde

PolarSpiral.PNG

Modular Forms

Computing modular forms

by William Stein

modformbasis.png

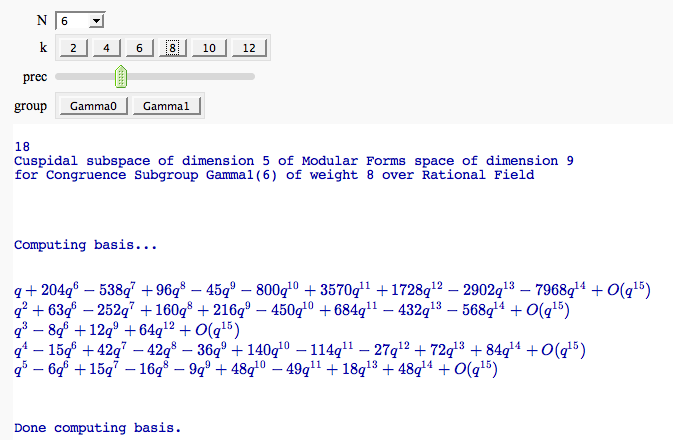
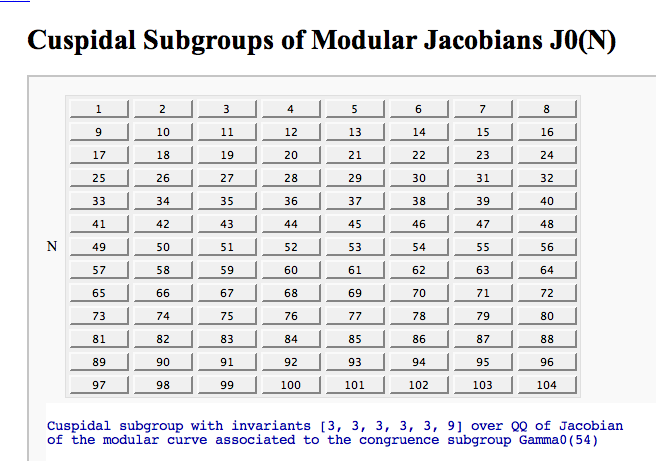
Computing the cuspidal subgroup

by William Stein

cuspgroup.png

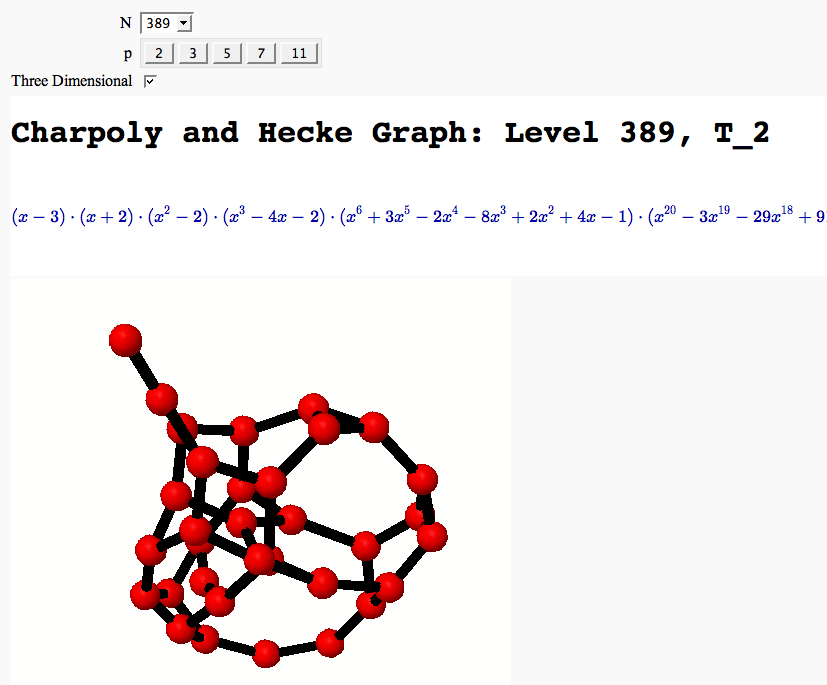
A Charpoly and Hecke Operator Graph FIXME

by William Stein

heckegraph.png

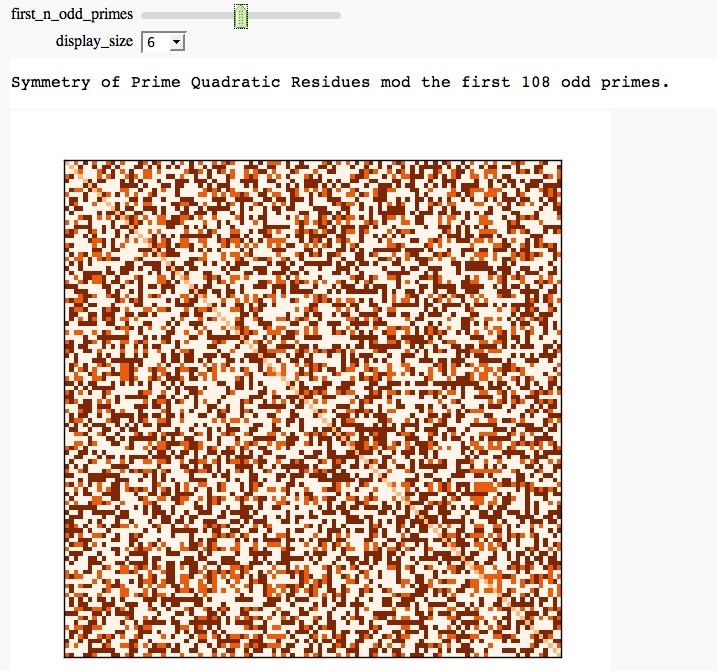
Modular Arithmetic

Quadratic Residue Table FIXME

by Emily Kirkman

quadres.png

quadresbig.png

Cubic Residue Table FIXME

by Emily Kirkman

cubres.png

Cyclotomic Fields

Gauss and Jacobi Sums in Complex Plane

by Emily Kirkman

jacobising.png

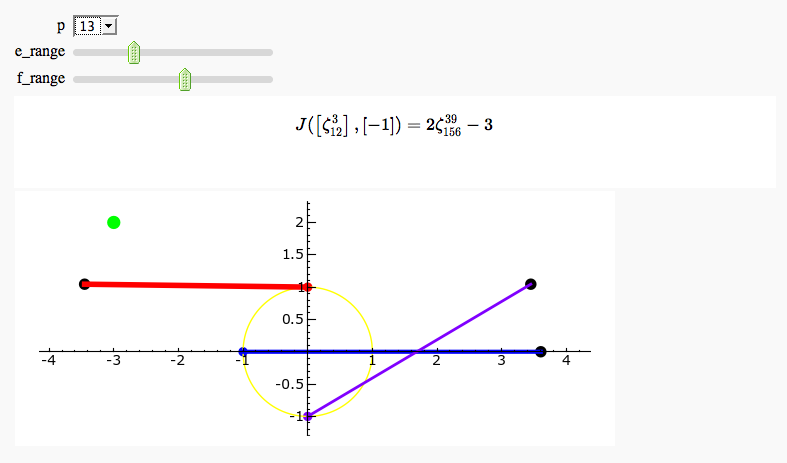
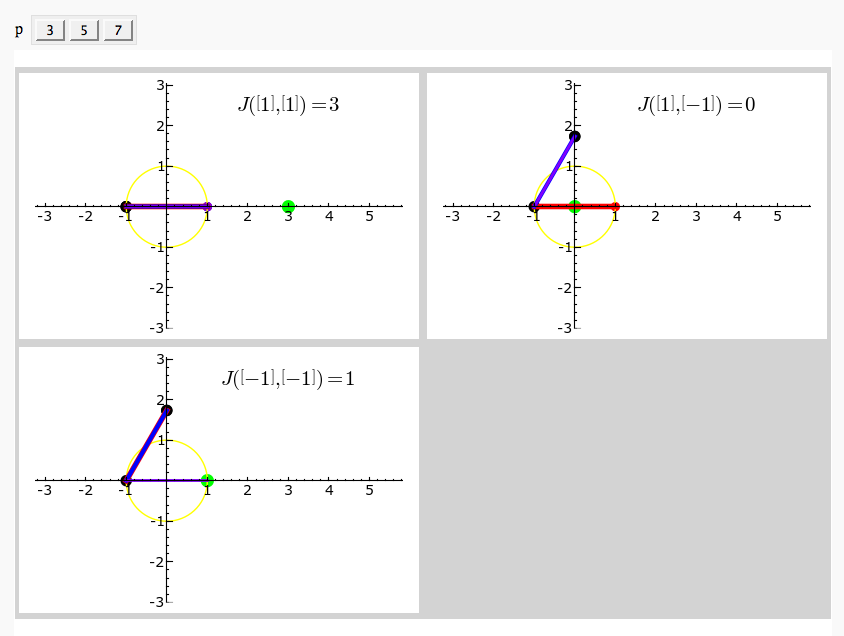
Exhaustive Jacobi Plotter

by Emily Kirkman

jacobiexh.png

Elliptic Curves

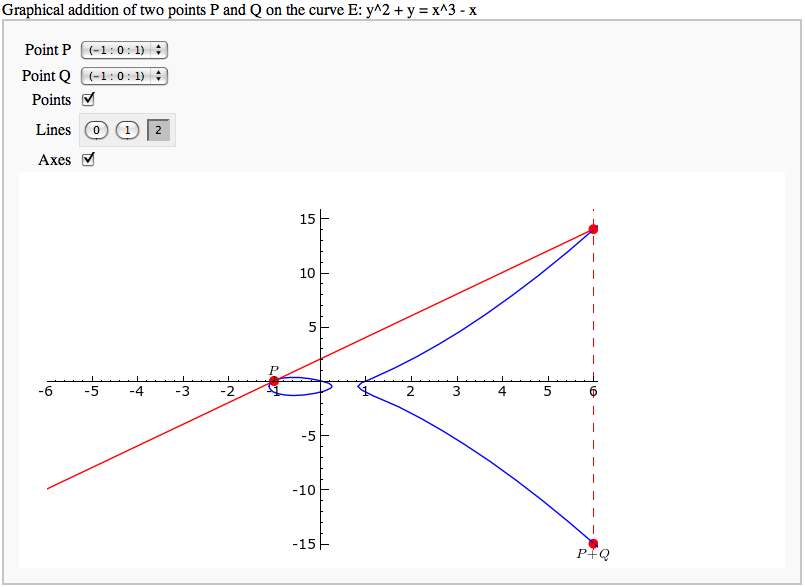
Adding points on an elliptic curve FIXME

by David Møller Hansen

PointAddEllipticCurve.png

Plotting an elliptic curve over a finite field

ellffplot.png

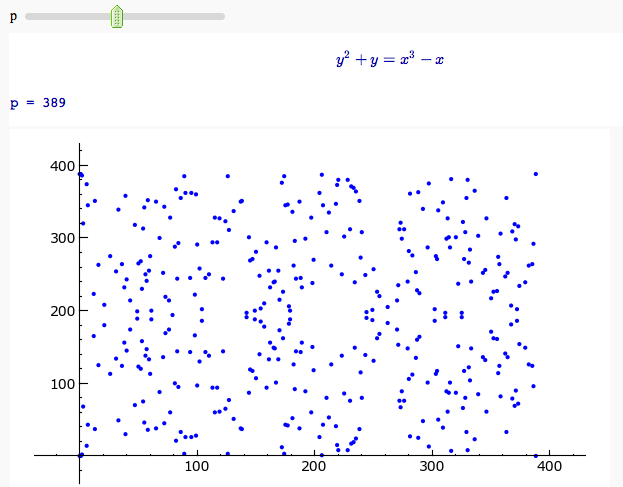
Cryptography

The Diffie-Hellman Key Exchange Protocol

by Timothy Clemans and William Stein

dh.png

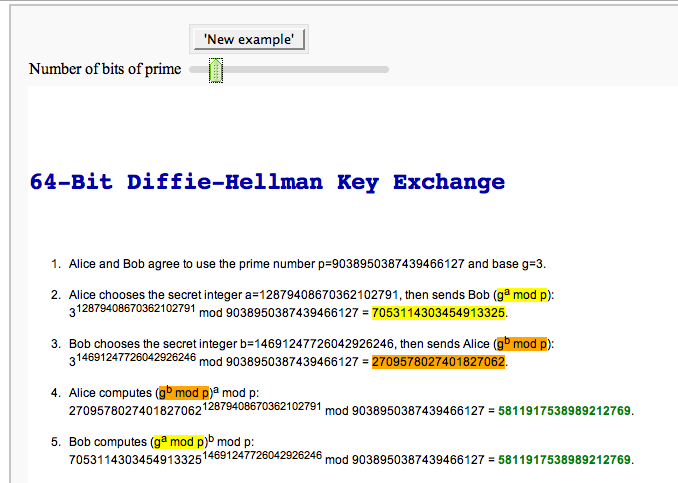
Other

Continued Fraction Plotter FIXME

by William Stein

contfracplot.png

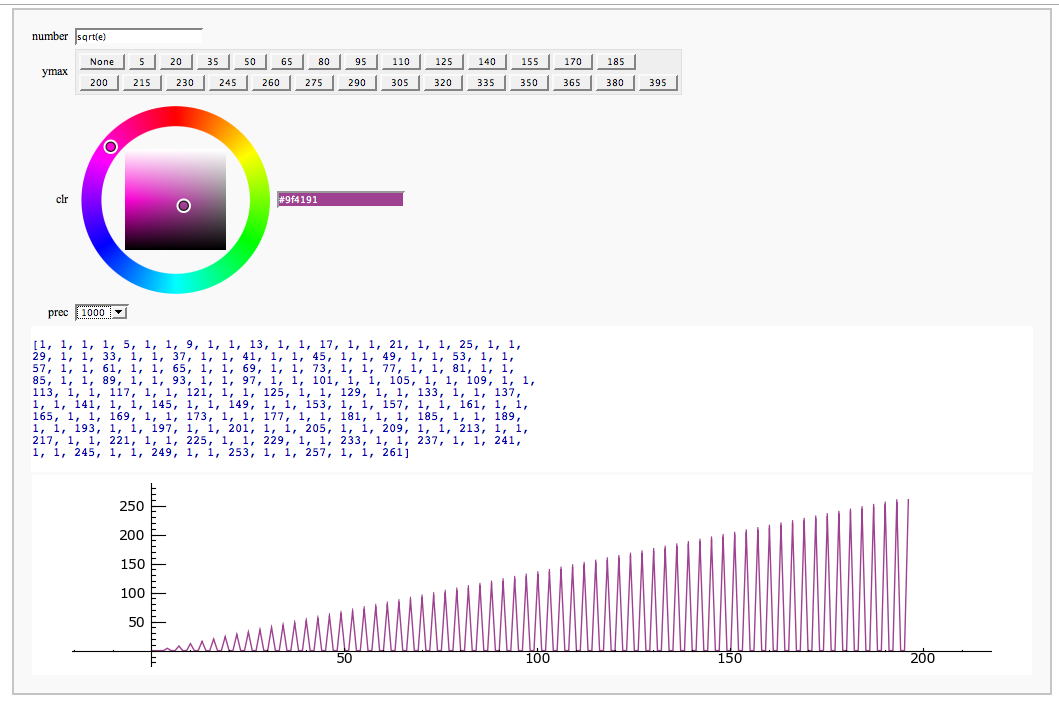
Computing Generalized Bernoulli Numbers

by William Stein (Sage-2.10.3)

bernoulli.png

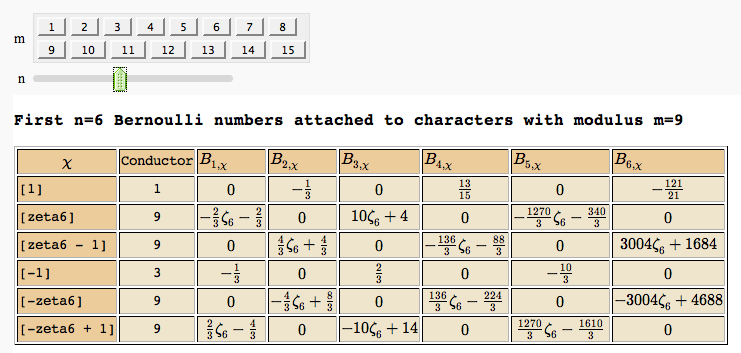
Fundamental Domains of SL_2(ZZ)

by Robert Miller

fund_domain.png

interact/number_theory (last edited 2020-06-14 09:10:48 by chapoton)