|
Size: 30302
Comment:
|
Size: 33100
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 7: | Line 7: |
| {{{ | {{{#!sagecell |
| Line 18: | Line 18: |
| {{{ | {{{#!sagecell |
| Line 51: | Line 51: |
| g += line([(j*2-len(cur),-i), ((k*2)-len(rows[i-1]),-i+1)], | g += line([(j*2-len(cur),-i), ((k*2)-len(rows[i-1]),-i+1)], |
| Line 72: | Line 72: |
| {{{ | {{{#!sagecell |
| Line 86: | Line 86: |
| {{{ | {{{#!sagecell |
| Line 94: | Line 94: |
| == Prime Spiral - Square == | == Prime Spiral - Square FIXME == |
| Line 96: | Line 96: |
| {{{ | {{{#!sagecell |
| Line 101: | Line 101: |
| REFERENCES: | REFERENCES: |
| Line 106: | Line 106: |
| Weisstein, Eric W. "Prime-Generating Polynomial." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Prime-GeneratingPolynomial.html | Weisstein, Eric W. "Prime-Generating Polynomial." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Prime-GeneratingPolynomial.html |
| Line 114: | Line 114: |
| elif y<0 and -x >= y and y<x: return 4*(y+1)^2 -11*(y+1) + (start+7) +x | elif y<0 and -x >= y and y<x: return 4*(y+1)^2 -11*(y+1) + (start+7) +x |
| Line 117: | Line 117: |
| #Takes in an n and the start value of the spiral and gives its (x,y) coordinate | #Takes in an n and the start value of the spiral and gives its (x,y) coordinate |
| Line 119: | Line 119: |
| num = num - start +1 | num = num - start +1 |
| Line 121: | Line 121: |
| top = ceil(sqrt(num)) | top = ceil(sqrt(num)) |
| Line 126: | Line 126: |
| else: | else: |
| Line 133: | Line 133: |
| else: | else: |
| Line 145: | Line 145: |
| N = M.copy() | N = copy(M) |
| Line 149: | Line 149: |
| #These functions return an int based on where the t is located in the spiral |
#These functions return an int based on where the t is located in the spiral |
| Line 162: | Line 162: |
| if n !=0: x_cord, y_cord = find_xy(n, start) #Overrides the user given x and y coordinates | if n !=0: x_cord, y_cord = find_xy(n, start) #Overrides the user given x and y coordinates |
| Line 170: | Line 170: |
| Line 173: | Line 173: |
| if show_lines: for t in [(-size-1)..size+1]: |
if show_lines: for t in [(-size-1)..size+1]: |
| Line 176: | Line 176: |
| if m.is_pseudoprime(): main_list.add(m) | if m.is_pseudoprime(): main_list.add(m) |
| Line 181: | Line 181: |
| #This for loop changes the matrix by spiraling out from the center and changing each entry as it goes. It is faster than the find_xy function above. | #This for loop changes the matrix by spiraling out from the center and changing each entry as it goes. It is faster than the find_xy function above. |
| Line 186: | Line 186: |
| else: x-=1 | else: x-=1 |
| Line 188: | Line 188: |
| elif county < overcount: |
elif county < overcount: |
| Line 191: | Line 191: |
| else: y-=1 | else: y-=1 |
| Line 193: | Line 193: |
| else: | else: |
| Line 199: | Line 199: |
| if not invert and num in main_list: |
if not invert and num in main_list: |
| Line 207: | Line 207: |
| if n != 0: |
if n != 0: |
| Line 224: | Line 224: |
| else: | else: |
| Line 233: | Line 233: |
| {{{ @interact def polar_prime_spiral(start=1, end=2000, show_factors = false, highlight_primes = false, show_curves=true, n = 0): #For more information about the factors in the spiral, visit http://www.dcs.gla.ac.uk/~jhw/spirals/index.html by John Williamson. |
{{{#!sagecell @interact def polar_prime_spiral(start=1, end=2000, show_factors = false, highlight_primes = false, show_curves=true, n = 0): #For more information about the factors in the spiral, visit http://www.dcs.gla.ac.uk/~jhw/spirals/index.html by John Williamson. |
| Line 243: | Line 243: |
| Line 251: | Line 251: |
| R = points(list2, alpha = .1) #Faded Composites else: |
R = points(list2, alpha = .1) #Faded Composites else: |
| Line 259: | Line 259: |
| R=points(list2, hue = .1, pointsize = p_size) |
R=points(list2, hue = .1, pointsize = p_size) |
| Line 263: | Line 263: |
| Line 270: | Line 270: |
| Q = plot(W1+W2+W3+W4, alpha = .1) | Q = plot(W1+W2+W3+W4, alpha = .1) |
| Line 273: | Line 273: |
| if show_curves: | if show_curves: |
| Line 278: | Line 278: |
| if n > (floor(sqrt(n)))^2 and n <= (floor(sqrt(n)))^2 + floor(sqrt(n)): | if n > (floor(sqrt(n)))^2 and n <= (floor(sqrt(n)))^2 + floor(sqrt(n)): |
| Line 281: | Line 281: |
| else: | else: |
| Line 286: | Line 286: |
| def g(m): return (a*m^2+b*m+c); | def g(m): return (a*m^2+b*m+c); |
| Line 292: | Line 292: |
| c= c2; | c= c2; |
| Line 307: | Line 307: |
| {{{ j = 0 @interact def _(N=[1..100], k=selector([2,4,..,12],nrows=1), prec=(3..40), |
{{{#!sagecell @interact def _(N=[1..100], k=selector([2,4,..,12],nrows=1), prec=(3..40), |
| Line 313: | Line 312: |
| print j; global j; j += 1 | |
| Line 330: | Line 328: |
| {{{ | {{{#!sagecell |
| Line 343: | Line 341: |
| {{{ | {{{#!sagecell |
| Line 351: | Line 349: |
| G = Graph(T, multiedges=True, loops=not three_d) | G = DiGraph(T, multiedges=not three_d) if three_d: G.remove_loops() |
| Line 364: | Line 364: |
| == Quadratic Residue Table == | == Quadratic Residue Table FIXME == |
| Line 366: | Line 366: |
| {{{ | {{{#!sagecell |
| Line 417: | Line 417: |
| == Cubic Residue Table == | == Cubic Residue Table FIXME == |
| Line 419: | Line 419: |
| {{{ | {{{#!sagecell |
| Line 437: | Line 437: |
| if Mod(a,3)!=0 and Mod(b,3)==0: return True else: return False |
return Mod(a,3)!=0 and Mod(b,3)==0 |
| Line 475: | Line 472: |
| MP += line([(i,0),(i,r)], rgbcolor='black') | MP += line([(i,0),(i,r)], rgbcolor='black') |
| Line 503: | Line 500: |
| {{{ | {{{#!sagecell |
| Line 552: | Line 549: |
| S = circle((0,0),1,rgbcolor='yellow') \ + line([e_pt,e_gs_pt], rgbcolor='red', thickness=4) \ + line([f_pt,f_gs_pt], rgbcolor='blue', thickness=3) \ + line([ef_pt,ef_gs_pt], rgbcolor='purple',thickness=2) \ + point(e_pt,pointsize=50, rgbcolor='red') \ + point(f_pt,pointsize=50, rgbcolor='blue') \ + point(ef_pt,pointsize=50,rgbcolor='purple') \ + point(f_gs_pt,pointsize=75, rgbcolor='black') \ + point(e_gs_pt,pointsize=75, rgbcolor='black') \ + point(ef_gs_pt,pointsize=75, rgbcolor='black') \ + point(js_pt,pointsize=100,rgbcolor='green') |
S = circle((0,0),1,rgbcolor='yellow') S += line([e_pt,e_gs_pt], rgbcolor='red', thickness=4) S += line([f_pt,f_gs_pt], rgbcolor='blue', thickness=3) S += line([ef_pt,ef_gs_pt], rgbcolor='purple',thickness=2) S += point(e_pt,pointsize=50, rgbcolor='red') S += point(f_pt,pointsize=50, rgbcolor='blue') S += point(ef_pt,pointsize=50,rgbcolor='purple') S += point(f_gs_pt,pointsize=75, rgbcolor='black') S += point(e_gs_pt,pointsize=75, rgbcolor='black') S += point(ef_gs_pt,pointsize=75, rgbcolor='black') S += point(js_pt,pointsize=100,rgbcolor='green') |
| Line 564: | Line 561: |
| S += text('$J(%s,%s) = %s$'%(latex2(e),latex2(f),latex(js)), \ | S += text('$J(%s,%s) = %s$'%(latex2(e),latex2(f),latex(js)), |
| Line 583: | Line 580: |
| {{{ | {{{#!sagecell |
| Line 632: | Line 629: |
| S = circle((0,0),1,rgbcolor='yellow') \ + line([e_pt,e_gs_pt], rgbcolor='red', thickness=4) \ + line([f_pt,f_gs_pt], rgbcolor='blue', thickness=3) \ + line([ef_pt,ef_gs_pt], rgbcolor='purple',thickness=2) \ + point(e_pt,pointsize=50, rgbcolor='red') \ + point(f_pt,pointsize=50, rgbcolor='blue') \ + point(ef_pt,pointsize=50,rgbcolor='purple') \ + point(f_gs_pt,pointsize=75, rgbcolor='black') \ + point(e_gs_pt,pointsize=75, rgbcolor='black') \ + point(ef_gs_pt,pointsize=75, rgbcolor='black') \ + point(js_pt,pointsize=100,rgbcolor='green') |
S = circle((0,0),1,rgbcolor='yellow') S += line([e_pt,e_gs_pt], rgbcolor='red', thickness=4) S += line([f_pt,f_gs_pt], rgbcolor='blue', thickness=3) S += line([ef_pt,ef_gs_pt], rgbcolor='purple',thickness=2) S += point(e_pt,pointsize=50, rgbcolor='red') S += point(f_pt,pointsize=50, rgbcolor='blue') S += point(ef_pt,pointsize=50,rgbcolor='purple') S += point(f_gs_pt,pointsize=75, rgbcolor='black') S += point(e_gs_pt,pointsize=75, rgbcolor='black') S += point(ef_gs_pt,pointsize=75, rgbcolor='black') S += point(js_pt,pointsize=100,rgbcolor='green') |
| Line 644: | Line 641: |
| S += text('$J(%s,%s) = %s$'%(latex2(e),latex2(f),latex(js)), \ | S += text('$J(%s,%s) = %s$'%(latex2(e),latex2(f),latex(js)), |
| Line 656: | Line 653: |
| ga[i].save('j%d.PNG'%i,figsize=4,aspect_ratio=1, \ | ga[i].save('j%d.png'%i,figsize=4,aspect_ratio=1, |
| Line 662: | Line 659: |
| html('<table bgcolor=lightgrey cellpadding=2>') | s='<table bgcolor=lightgrey cellpadding=2>' |
| Line 664: | Line 661: |
| html('<tr><td align="center"><img src="cell://j%d.PNG"></td>'%(2*i)) html('<td align="center"><img src="cell://j%d.PNG"></td></tr>'%(2*i+1)) html('</table>') }}} |
s+='<tr><td align="center"><img src="cell://j%d.png"></td>'%(2*i) s+='<td align="center"><img src="cell://j%d.png"></td></tr>'%(2*i+1) s+='</table>' html(s)}}} |
| Line 675: | Line 672: |
| {{{ | {{{#!sagecell |
| Line 681: | Line 678: |
| else: | else: |
| Line 688: | Line 685: |
def line_from_curve_points(E,P,Q,style='-',rgb=(1,0,0),length=25): """ P,Q two points on an elliptic curve. Output is a graphic representation of the straight line intersecting with P,Q. """ # The function tangent to P=Q on E if P == Q: if P[2]==0: return line([(1,-length),(1,length)],linestyle=style,rgbcolor=rgb) else: # Compute slope of the curve E in P l=-(3*P[0]^2 + 2*E.a2()*P[0] + E.a4() - E.a1()*P[1])/((-2)*P[1] - E.a1()*P[0] - E.a3()) f(x) = l * (x - P[0]) + P[1] return plot(f(x),-length,length,linestyle=style,rgbcolor=rgb) # Trivial case of P != R where P=O or R=O then we get the vertical line from the other point elif P[2] == 0: return line([(Q[0],-length),(Q[0],length)],linestyle=style,rgbcolor=rgb) elif Q[2] == 0: return line([(P[0],-length),(P[0],length)],linestyle=style,rgbcolor=rgb) # Non trivial case where P != R else: # Case where x_1 = x_2 return vertical line evaluated in Q if P[0] == Q[0]: return line([(P[0],-length),(P[0],length)],linestyle=style,rgbcolor=rgb) #Case where x_1 != x_2 return line trough P,R evaluated in Q" l=(Q[1]-P[1])/(Q[0]-P[0]) f(x) = l * (x - P[0]) + P[1] return plot(f(x),-length,length,linestyle=style,rgbcolor=rgb) |
|
| Line 690: | Line 718: |
| curve = E.plot(rgbcolor = (0,0,1),xmin=25,xmax=25,plot_points=300) | curve = E.plot(rgbcolor = (0,0,1),xmin=-5,xmax=5,plot_points=300) |
| Line 716: | Line 744: |
def line_from_curve_points(E,P,Q,style='-',rgb=(1,0,0),length=25): """ P,Q two points on an elliptic curve. Output is a graphic representation of the straight line intersecting with P,Q. """ # The function tangent to P=Q on E if P == Q: if P[2]==0: return line([(1,-length),(1,length)],linestyle=style,rgbcolor=rgb) else: # Compute slope of the curve E in P l=-(3*P[0]^2 + 2*E.a2()*P[0] + E.a4() - E.a1()*P[1])/((-2)*P[1] - E.a1()*P[0] - E.a3()) f(x) = l * (x - P[0]) + P[1] return plot(f(x),-length,length,linestyle=style,rgbcolor=rgb) # Trivial case of P != R where P=O or R=O then we get the vertical line from the other point elif P[2] == 0: return line([(Q[0],-length),(Q[0],length)],linestyle=style,rgbcolor=rgb) elif Q[2] == 0: return line([(P[0],-length),(P[0],length)],linestyle=style,rgbcolor=rgb) # Non trivial case where P != R else: # Case where x_1 = x_2 return vertical line evaluated in Q if P[0] == Q[0]: return line([(P[0],-length),(P[0],length)],linestyle=style,rgbcolor=rgb) #Case where x_1 != x_2 return line trough P,R evaluated in Q" l=(Q[1]-P[1])/(Q[0]-P[0]) f(x) = l * (x - P[0]) + P[1] return plot(f(x),-length,length,linestyle=style,rgbcolor=rgb) |
|
| Line 751: | Line 749: |
| {{{ | {{{#!sagecell |
| Line 766: | Line 764: |
| {{{ | {{{#!sagecell |
| Line 780: | Line 778: |
| print """ <html> |
html(""" |
| Line 805: | Line 802: |
| </ol></html> """ % (bits, p, g, a, g, a, p, (g^a), b, g, b, p, (g^b), (g^b), a, p, (g^ b)^a, g^a, b, p, (g^a)^b) |
</ol> """ % (bits, p, g, a, g, a, p, (g^a), b, g, b, p, (g^b), (g^b), a, p, (g^ b)^a, g^a, b, p, (g^a)^b)) |
| Line 817: | Line 814: |
| {{{ @interact def _(number=e, ymax=selector([None,5,20,..,400],nrows=2), clr=Color('purple'), prec=[500,1000,..,5000]): |
{{{#!sagecell @interact def _(number=e, ymax=selector([5,20,..,400],nrows=2), clr=Color('purple'), prec=[500,1000,..,5000]): |
| Line 827: | Line 824: |
| {{{ | {{{#!sagecell |
| Line 848: | Line 845: |
| {{{ | {{{#!sagecell |
| Line 856: | Line 853: |
| def _(gen = selector(['t+1', 't-1', '-1/t'], nrows=1)): | def _(gen = selector(['t+1', 't-1', '-1/t'], buttons=True,nrows=1)): |
| Line 874: | Line 871: |
= Multiple Zeta Values = by Akhilesh P. == Word to composition == {{{#!sagecell @interact def _( weight=(7,(2..30))): n=weight a=[0 for i in range(n-1)] a.append(1) @interact def _(v=('word', input_grid(1, n, default=[a], to_value=lambda x: vector(flatten(x))))): a=[v[i] for i in range(len(v))] def bintocomp(a): b=[] count=1 for j in range(len(a)): if(a[j]==0): count=count+1 else: b.append(count) count=1 return(b) print "Composition is ",bintocomp(a) }}} {{attachment:akhi2.png}} == Composition to Word == {{{#!sagecell @interact def _( Depth=(7,(1..30))): n=Depth a=[] a.append(2) a=[1 for i in range(1,n)] @interact def _(v=('composition', input_grid(1, n, default=[a], to_value=lambda x: vector(flatten(x))))): a=[v[i] for i in range(len(v))] def comptobin(a): word=[] for i in range(len(a)): word=word+[0]*(a[i]-1)+[1] return(word) print "Word is is ",comptobin(a) }}} {{attachment:akhi2.png}} == Computing Multiple Zeta values == {{{#!sagecell R=RealField(10) @interact def _( weight=(5,(2..20))): n=weight a=[0 for i in range(n-1)] a.append(1) @interact def _(v=('word', input_grid(1, n, default=[a], to_value=lambda x: vector(flatten(x)))), accuracy=(100..100000)): D=accuracy a=[v[i] for i in range(len(v))] DD=int(3.321928*D)+int(R(log(3.321928*D))/R(log(10)))+4 RIF=RealIntervalField(DD) def Li(word): n=int(DD*log(10)/log(2))+1 B=[] L=[] S=[] count=-1 k=len(word) for i in range(k): B.append(RIF('0')) L.append(RIF('0')) if(word[i]==1 and i<k-1): S.append(RIF('0')) count=count+1 T=RIF('1') for m in range(n): T=T/2 B[k-1]=RIF('1')/(m+1) j=count for i in range(k-2,-1,-1): if(word[i]==0): B[i]=B[i+1]/(m+1) elif(word[i]==1): B[i]=S[j]/(m+1) S[j]=S[j]+B[i+1] j=j-1 L[i]=T*B[i]+L[i] L[k-1]=T*B[k-1]+L[k-1] return(L) def dual(a): b=list() b=a b=b[::-1] for i in range(len(b)): b[i]=1-b[i] return(b) def zeta(a): b=dual(a) l1=Li(a)+[1] l2=Li(b)+[1] Z=RIF('0') for i in range(len(l1)): Z=Z+l1[i]*l2[len(a)-i] return(Z) print zeta(a) }}} {{attachment:akhi1.png}} |
Contents
Integer Factorization
Divisibility Poset
by William Stein
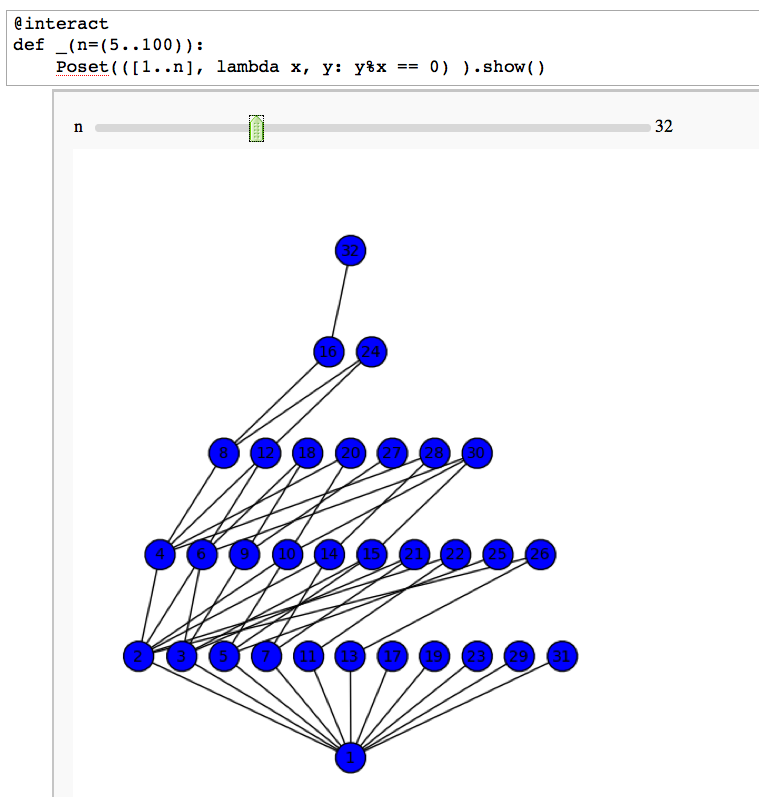
Factor Trees
by William Stein
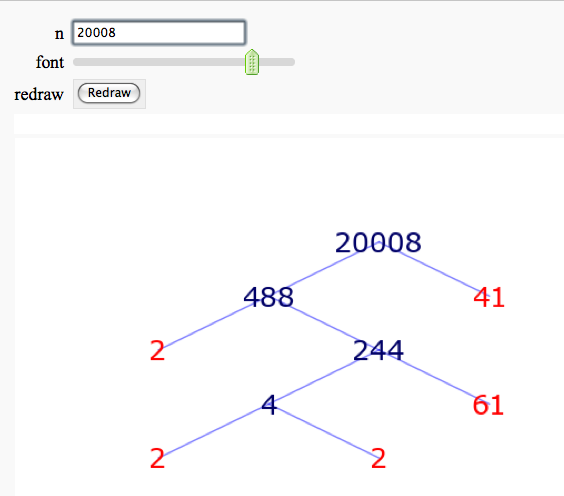
More complicated demonstration using Mathematica: http://demonstrations.wolfram.com/FactorTrees/
Factoring an Integer
by Timothy Clemans
Sage implementation of the Mathematica demonstration of the same name. http://demonstrations.wolfram.com/FactoringAnInteger/
Prime Numbers
Illustrating the prime number theorem
by William Stein
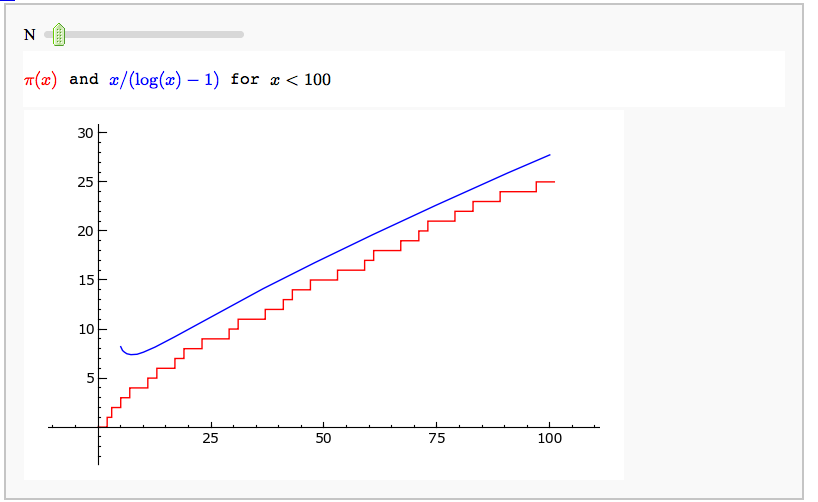
Prime Spiral - Square FIXME
by David Runde
Prime Spiral - Polar
by David Runde
Modular Forms
Computing modular forms
by William Stein
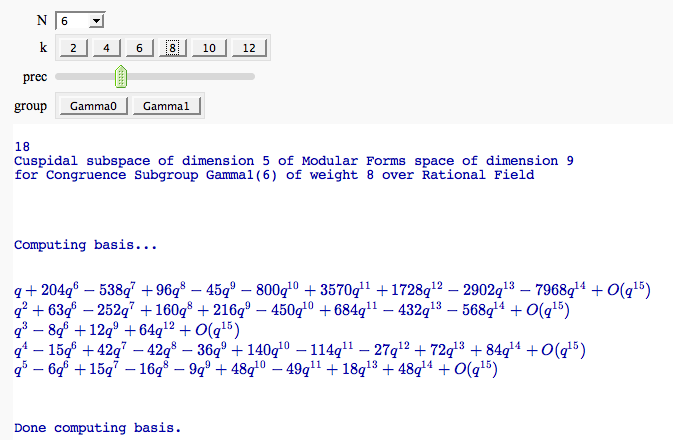
Computing the cuspidal subgroup
by William Stein
A Charpoly and Hecke Operator Graph
by William Stein
Modular Arithmetic
Quadratic Residue Table FIXME
by Emily Kirkman

Cubic Residue Table FIXME
by Emily Kirkman

Cyclotomic Fields
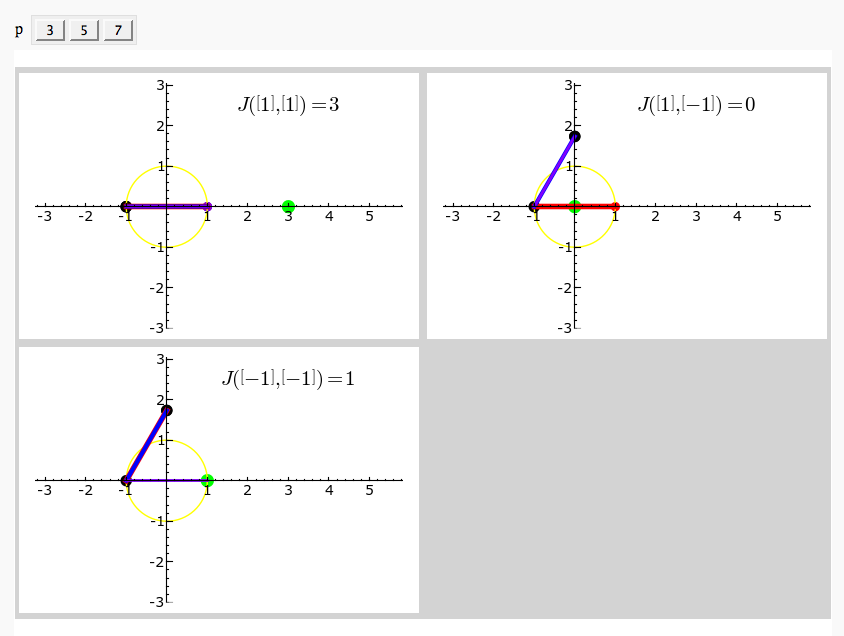
Gauss and Jacobi Sums in Complex Plane
by Emily Kirkman
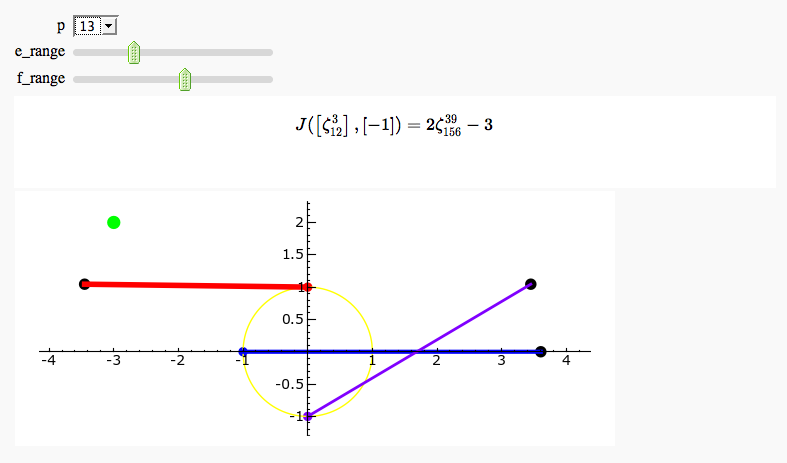
Exhaustive Jacobi Plotter
by Emily Kirkman
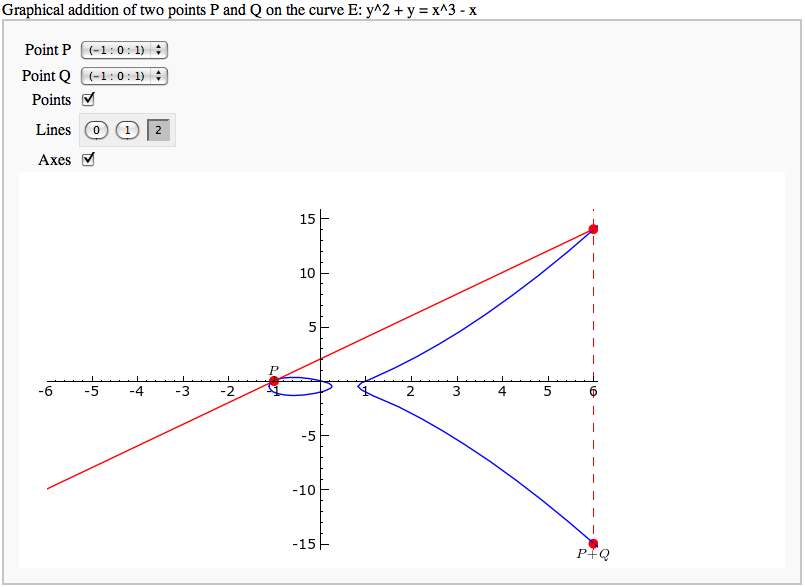
Elliptic Curves
Adding points on an elliptic curve
by David Møller Hansen
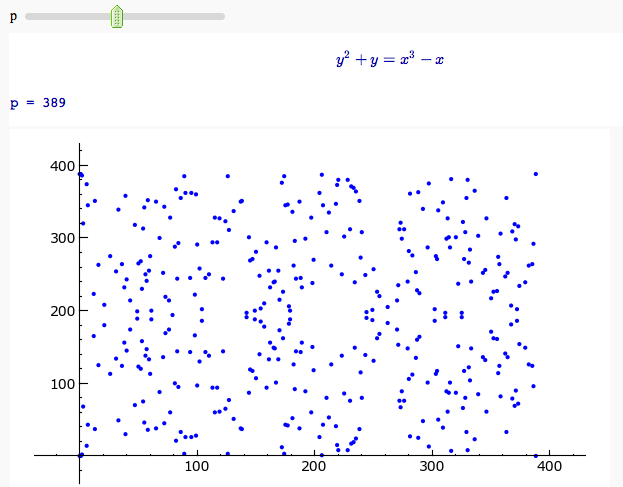
Plotting an elliptic curve over a finite field
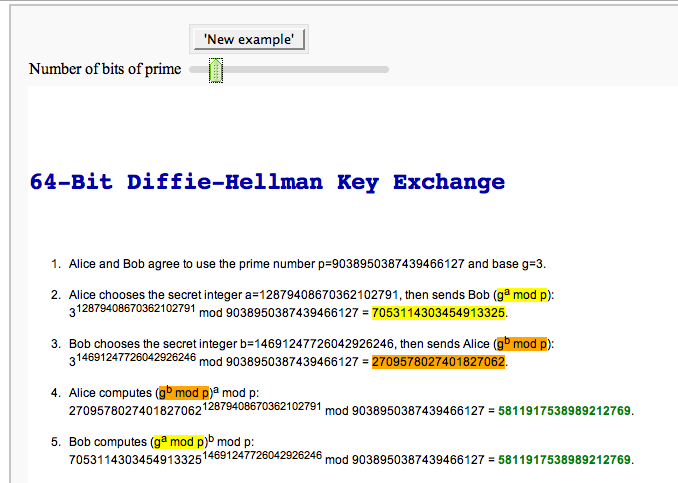
Cryptography
The Diffie-Hellman Key Exchange Protocol
by Timothy Clemans and William Stein
Other
Continued Fraction Plotter
by William Stein
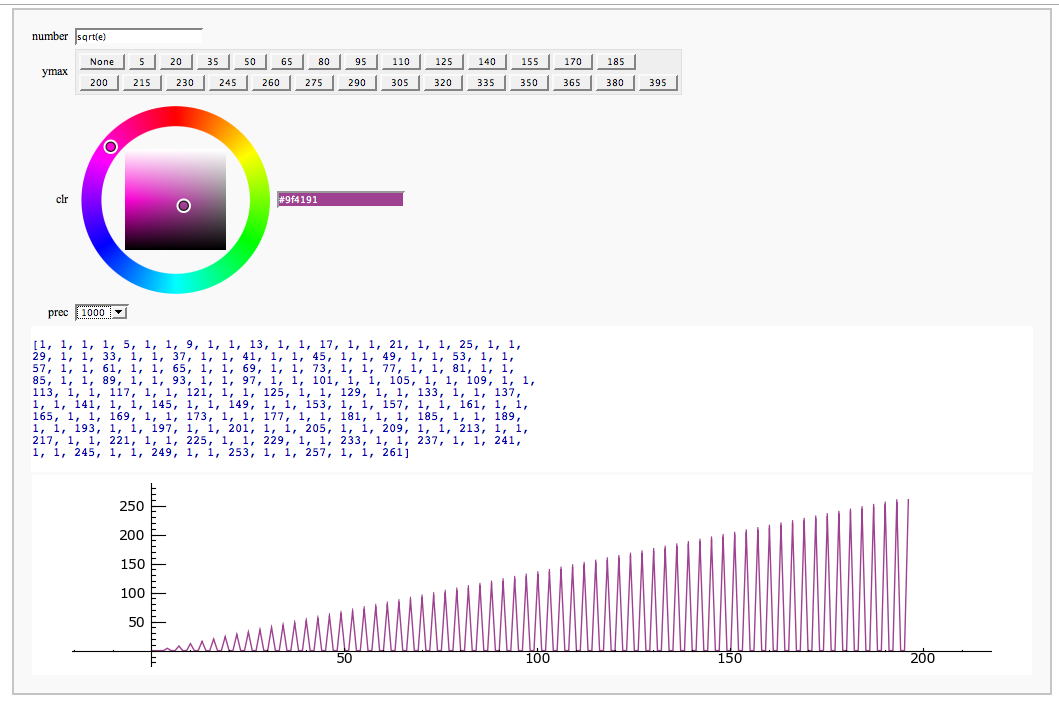
Computing Generalized Bernoulli Numbers
by William Stein (Sage-2.10.3)
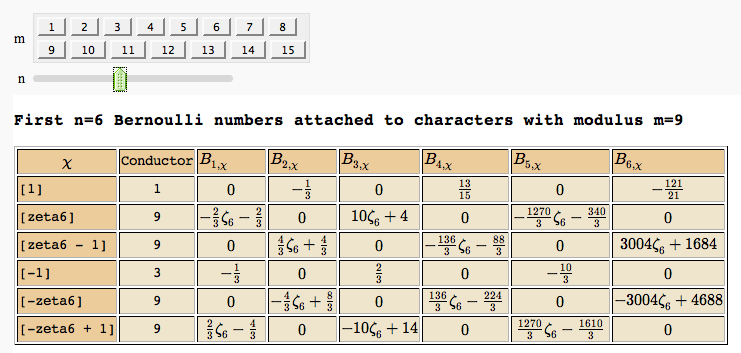
Fundamental Domains of SL_2(ZZ)
by Robert Miller
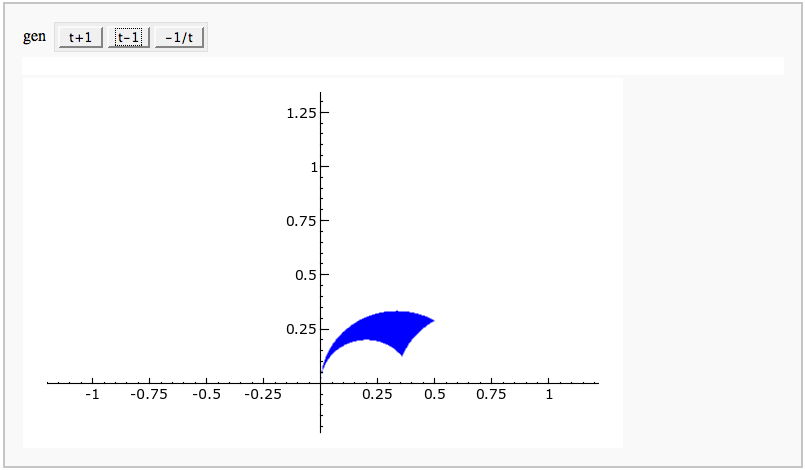
Multiple Zeta Values
by Akhilesh P.
Word to composition

Composition to Word

Computing Multiple Zeta values

