|
Size: 33102
Comment:
|
Size: 45946
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 915: | Line 915: |
| print "Word is is ",comptobin(a) }}} {{attachment:akhi2.png}} |
print "Word is ",comptobin(a) }}} {{attachment:akhi3.png}} == Dual of a Word == {{{#!sagecell @interact def _( weight=(7,(2..30))): n=weight a=[0 for i in range(n-1)] a.append(1) @interact def _(v=('word', input_grid(1, n, default=[a], to_value=lambda x: vector(flatten(x))))): a=[v[i] for i in range(len(v))] def dual(a): b=list() b=a b=b[::-1] for i in range(len(b)): b[i]=1-b[i] return(b) print "Dual word is ",dual(a) }}} {{attachment:akhi4.png}} |
| Line 922: | Line 944: |
| === Word Input === | |
| Line 981: | Line 1004: |
| === Composition Input === {{{#!sagecell R=RealField(10) @interact def _( Depth=(5,(2..20))): n=Depth a=[2] a=a+[1 for i in range(n-1)] @interact def _(v=('Composition', input_grid(1, n, default=[a], to_value=lambda x: vector(flatten(x)))), accuracy=(100..100000)): D=accuracy a=[v[i] for i in range(len(v))] def comptobin(a): word=[] for i in range(len(a)): word=word+[0]*(a[i]-1)+[1] return(word) a=comptobin(a) DD=int(3.321928*D)+int(R(log(3.321928*D))/R(log(10)))+4 RIF=RealIntervalField(DD) def Li(word): n=int(DD*log(10)/log(2))+1 B=[] L=[] S=[] count=-1 k=len(word) for i in range(k): B.append(RIF('0')) L.append(RIF('0')) if(word[i]==1 and i<k-1): S.append(RIF('0')) count=count+1 T=RIF('1') for m in range(n): T=T/2 B[k-1]=RIF('1')/(m+1) j=count for i in range(k-2,-1,-1): if(word[i]==0): B[i]=B[i+1]/(m+1) elif(word[i]==1): B[i]=S[j]/(m+1) S[j]=S[j]+B[i+1] j=j-1 L[i]=T*B[i]+L[i] L[k-1]=T*B[k-1]+L[k-1] return(L) def dual(a): b=list() b=a b=b[::-1] for i in range(len(b)): b[i]=1-b[i] return(b) def zeta(a): b=dual(a) l1=Li(a)+[1] l2=Li(b)+[1] Z=RIF('0') for i in range(len(l1)): Z=Z+l1[i]*l2[len(a)-i] return(Z) print zeta(a) }}} {{attachment:akhi5.png}} == Shuffle product of two Words == {{{#!sagecell @interact def _( w1=(2,(2..20)), w2=(2,(2..20))): a=[0] b=[0 for i in range(w2-1)] a=a+[1 for i in range(1,w1)] b=b+[1] import itertools #this program gives the list of all binary words of weight n and depth k @interact def _(v1=('word1', input_grid(1, w1, default=[a], to_value=lambda x: vector(flatten(x)))), v2=('word2', input_grid(1, w2, default=[b], to_value=lambda x: vector(flatten(x))))): a=[v1[i] for i in range(len(v1))] b=[v2[i] for i in range(len(v2))] def kbits(n, k): result = [] for bits in itertools.combinations(range(n), k): s = ['0'] * n for bit in bits: s[bit] = '1' result.append(''.join(s)) return result def sort(a,l,m): b=[] n=len(a) for i in range(n): b.append(a[i]) for j in range(l-1,-1,-1): k=0 for t in range(m+1): for i in range(n): if(a[i][j]== t): b[k]=a[i] k=k+1 for i in range(n): a[i]=b[i] return(a) def count(a): n=len(a) b=[] b.append(a[0]) m=[] m.append(1) c=0 for i in range(1,n): if(a[i]==a[i-1]): m[c]=m[c]+1 else: b.append(a[i]) m.append(1) c=c+1 return(b,m) def shuffle(a,b): r=len(a) s=len(b) # Generating an array of strings containing all combinations of weight r+s and depth s M=kbits(r+s,s) n=len(M) a1= [] for i in range(n): a1.append(list(M[i])) # The zeroes are replaced by the entries of a and the ones by the entries of b a2= [] for i in range(n): a2.append([]) count0=0 count1=0 for j in range(s+r): if(a1[i][j]=='0'): a2[i].append(a[count0]) count0=count0+1 if(a1[i][j]=='1'): a2[i].append(b[count1]) count1=count1+1 # Reordering in lexicographic order the entries of a2: this is done by first reordering them according to the last digit, then the next to last digit, etc a3=sort(a2,r+s,max(a+b+[0])) # Getting the same list without repetitions and with multiplicities a4=count(a3) return(a4) c=shuffle(a,b) for i in range(len(c[0])-1): print c[1][i],"*",c[0][i] ,"+ ", print c[1][len(c[0])-1],"*",c[0][len(c[0])-1] }}} {{attachment:akhi6.png}} == Shuffle Regularization at 0 == {{{#!sagecell @interact def _( w=(2,(2..20))): a=[0] a=a+[1 for i in range(1,w)] import itertools #this program gives the list of all binary words of weight n and depth k @interact def _(v=('word', input_grid(1, w, default=[a], to_value=lambda x: vector(flatten(x))))): a=[v[i] for i in range(len(v))] def kbits(n, k): result = [] for bits in itertools.combinations(range(n), k): s = ['0'] * n for bit in bits: s[bit] = '1' result.append(''.join(s)) return result def sort(a,l,m): b=[] n=len(a) for i in range(n): b.append(a[i]) for j in range(l-1,-1,-1): k=0 for t in range(m+1): for i in range(n): if(a[i][j]== t): b[k]=a[i] k=k+1 for i in range(n): a[i]=b[i] return(a) def sort1(a,l,m): b=[] b.append([]) b.append([]) n=len(a[0]) for i in range(n): b[0].append(a[0][i]) b[1].append(a[1][i]) for j in range(l-1,-1,-1): k=0 for t in range(m+1): for i in range(n): if(a[0][i][j]== t): b[0][k]=a[0][i] b[1][k]=a[1][i] k=k+1 for i in range(n): a[0][i]=b[0][i] a[1][i]=b[1][i] return(a) def count(a): n=len(a) b=[] b.append(a[0]) m=[] m.append(1) c=0 for i in range(1,n): if(a[i]==a[i-1]): m[c]=m[c]+1 else: b.append(a[i]) m.append(1) c=c+1 return(b,m) def count1(a): n=len(a[0]) b=[] b.append([]) b.append([]) b[0].append(a[0][0]) b[1].append(a[1][0]) c=0 for i in range(1,n): if(a[0][i]==a[0][i-1]): b[1][c]=b[1][c]+a[1][i] else: b[0].append(a[0][i]) b[1].append(a[1][i]) c=c+1 return(b) def shuffle(a,b): r=len(a) s=len(b) # Generating an array of strings containing all combinations of weight r+s and depth s M=kbits(r+s,s) n=len(M) a1= [] for i in range(n): a1.append(list(M[i])) # The zeroes are replaced by the entries of a and the ones by the entries of b a2= [] for i in range(n): a2.append([]) count0=0 count1=0 for j in range(s+r): if(a1[i][j]=='0'): a2[i].append(a[count0]) count0=count0+1 if(a1[i][j]=='1'): a2[i].append(b[count1]) count1=count1+1 # Reordering in lexicographic order the entries of a2: this is done by first reordering them according to the last digit, then the next to last digit, etc a3=sort(a2,r+s,max(a+b+[0])) # Getting the same list without repetitions and with multiplicities a4=count(a3) return(a4) def Regshuf0(a): r=[] r.append([]) r.append([]) t=0 c=1 for i in range(len(a)+1): if(t==0): b=shuffle(a[:len(a)-i],a[len(a)-i:]) for j in range(len(b[0])): r[0].append(b[0][j]) r[1].append(b[1][j]*c) c=-c if(i<len(a)): if(a[len(a)-1-i]==1): t=1 r=sort1(r,len(a),max(a+[0])) r=count1(r) rg=[] rg.append([]) rg.append([]) for i in range(len(r[0])): if(r[1][i] is not 0): rg[0].append(r[0][i]) rg[1].append(r[1][i]) return(rg) c=Regshuf0(a) for i in range(len(c[0])-1): if(c[1][i] != 0): print c[1][i],"*",c[0][i] ,"+ ", if(c[1][len(c[0])-1] != 0): print c[1][len(c[0])-1],"*",c[0][len(c[0])-1] }}} {{attachment:akhi7.png}} == Shuffle Regularization at 1 == {{{#!sagecell @interact def _( w=(2,(2..20))): a=[0] a=a+[1 for i in range(1,w)] import itertools #this program gives the list of all binary words of weight n and depth k @interact def _(v=('word', input_grid(1, w, default=[a], to_value=lambda x: vector(flatten(x))))): a=[v[i] for i in range(len(v))] def kbits(n, k): result = [] for bits in itertools.combinations(range(n), k): s = ['0'] * n for bit in bits: s[bit] = '1' result.append(''.join(s)) return result def sort(a,l,m): b=[] n=len(a) for i in range(n): b.append(a[i]) for j in range(l-1,-1,-1): k=0 for t in range(m+1): for i in range(n): if(a[i][j]== t): b[k]=a[i] k=k+1 for i in range(n): a[i]=b[i] return(a) def sort1(a,l,m): b=[] b.append([]) b.append([]) n=len(a[0]) for i in range(n): b[0].append(a[0][i]) b[1].append(a[1][i]) for j in range(l-1,-1,-1): k=0 for t in range(m+1): for i in range(n): if(a[0][i][j]== t): b[0][k]=a[0][i] b[1][k]=a[1][i] k=k+1 for i in range(n): a[0][i]=b[0][i] a[1][i]=b[1][i] return(a) def count(a): n=len(a) b=[] b.append(a[0]) m=[] m.append(1) c=0 for i in range(1,n): if(a[i]==a[i-1]): m[c]=m[c]+1 else: b.append(a[i]) m.append(1) c=c+1 return(b,m) def count1(a): n=len(a[0]) b=[] b.append([]) b.append([]) b[0].append(a[0][0]) b[1].append(a[1][0]) c=0 for i in range(1,n): if(a[0][i]==a[0][i-1]): b[1][c]=b[1][c]+a[1][i] else: b[0].append(a[0][i]) b[1].append(a[1][i]) c=c+1 return(b) def shuffle(a,b): r=len(a) s=len(b) # Generating an array of strings containing all combinations of weight r+s and depth s M=kbits(r+s,s) n=len(M) a1= [] for i in range(n): a1.append(list(M[i])) # The zeroes are replaced by the entries of a and the ones by the entries of b a2= [] for i in range(n): a2.append([]) count0=0 count1=0 for j in range(s+r): if(a1[i][j]=='0'): a2[i].append(a[count0]) count0=count0+1 if(a1[i][j]=='1'): a2[i].append(b[count1]) count1=count1+1 # Reordering in lexicographic order the entries of a2: this is done by first reordering them according to the last digit, then the next to last digit, etc a3=sort(a2,r+s,max(a+b+[0])) # Getting the same list without repetitions and with multiplicities a4=count(a3) return(a4) def Regshuf1(a): r=[] r.append([]) r.append([]) t=0 c=1 for i in range(len(a)+1): if(t==0): b=shuffle(a[:i],a[i:]) for j in range(len(b[0])): r[0].append(b[0][j]) r[1].append(b[1][j]*c) c=-c if(i<len(a)): if(a[i]==0): t=1 r=sort1(r,len(a),max(a+[0])) r=count1(r) rg=[] rg.append([]) rg.append([]) for i in range(len(r[0])): if(r[1][i] is not 0): rg[0].append(r[0][i]) rg[1].append(r[1][i]) return(rg) c=Regshuf0(a) for i in range(len(c[0])-1): if(c[1][i] != 0): print c[1][i],"*",c[0][i] ,"+ ", if(c[1][len(c[0])-1] != 0): print c[1][len(c[0])-1],"*",c[0][len(c[0])-1] }}} {{attachment:akhi8.png}} |
Contents
Integer Factorization
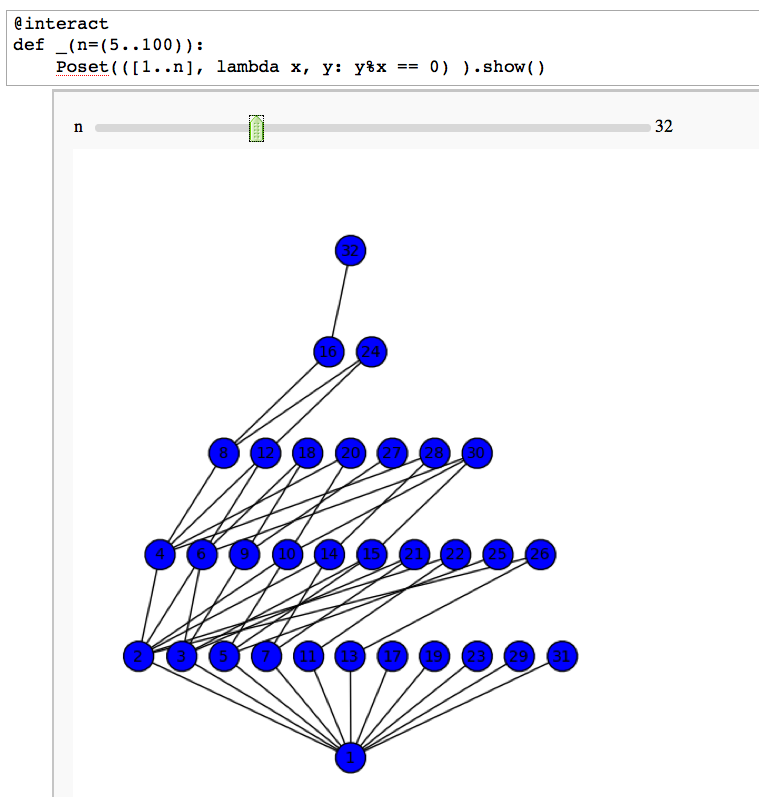
Divisibility Poset
by William Stein
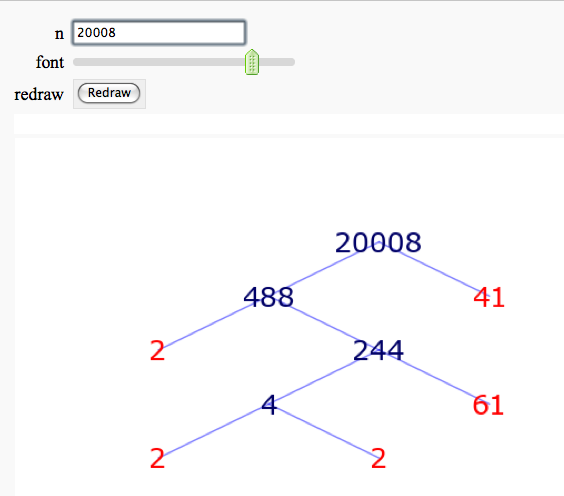
Factor Trees
by William Stein
More complicated demonstration using Mathematica: http://demonstrations.wolfram.com/FactorTrees/
Factoring an Integer
by Timothy Clemans
Sage implementation of the Mathematica demonstration of the same name. http://demonstrations.wolfram.com/FactoringAnInteger/
Prime Numbers
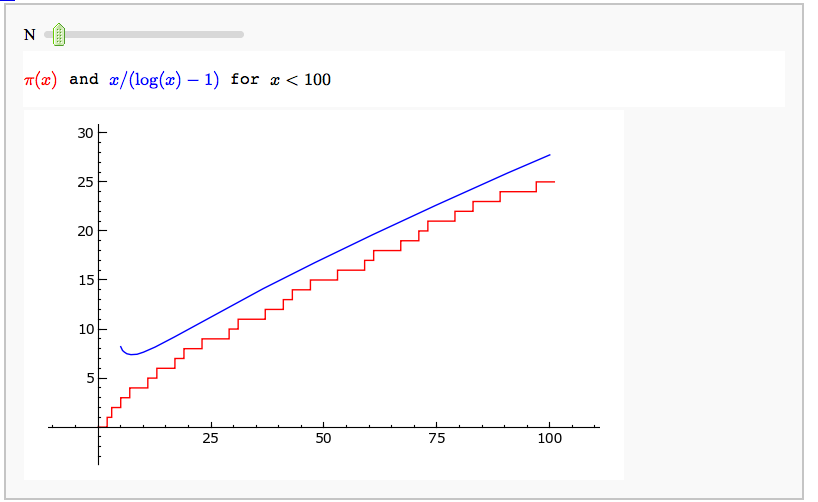
Illustrating the prime number theorem
by William Stein
Prime Spiral - Square FIXME
by David Runde
Prime Spiral - Polar
by David Runde
Modular Forms
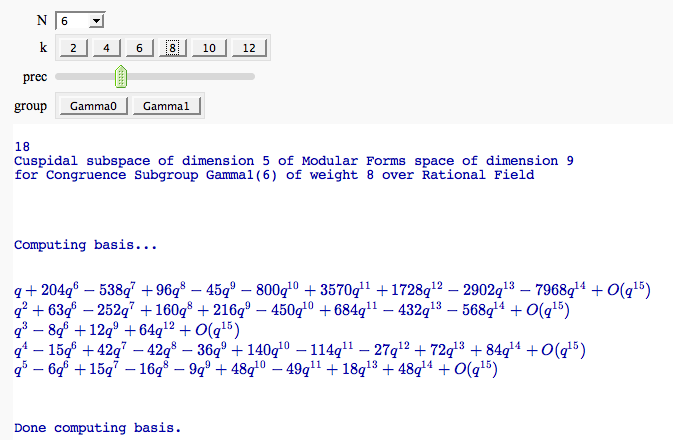
Computing modular forms
by William Stein
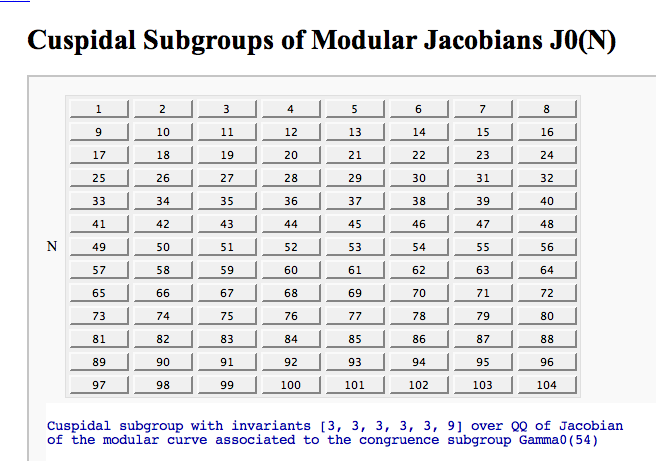
Computing the cuspidal subgroup
by William Stein
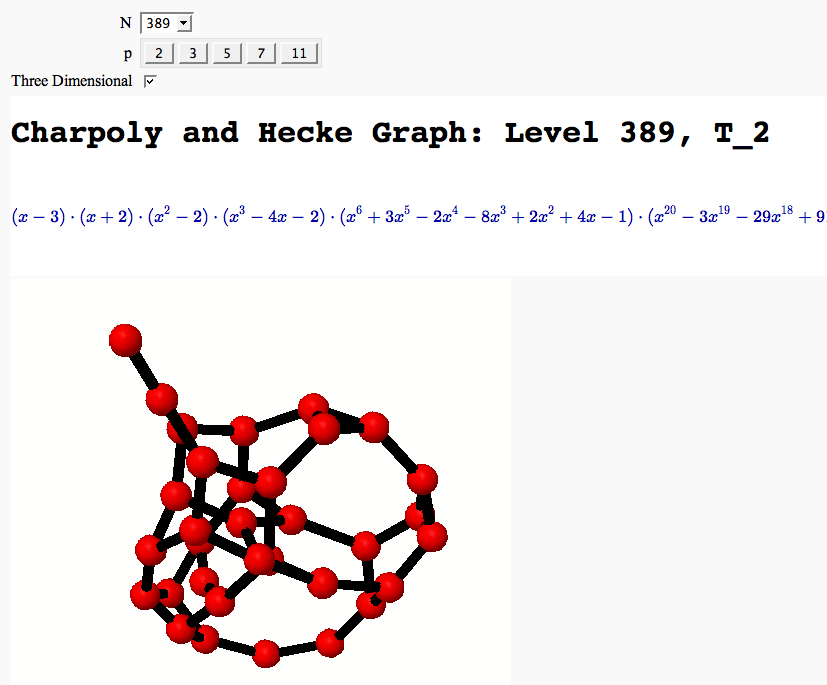
A Charpoly and Hecke Operator Graph
by William Stein
Modular Arithmetic
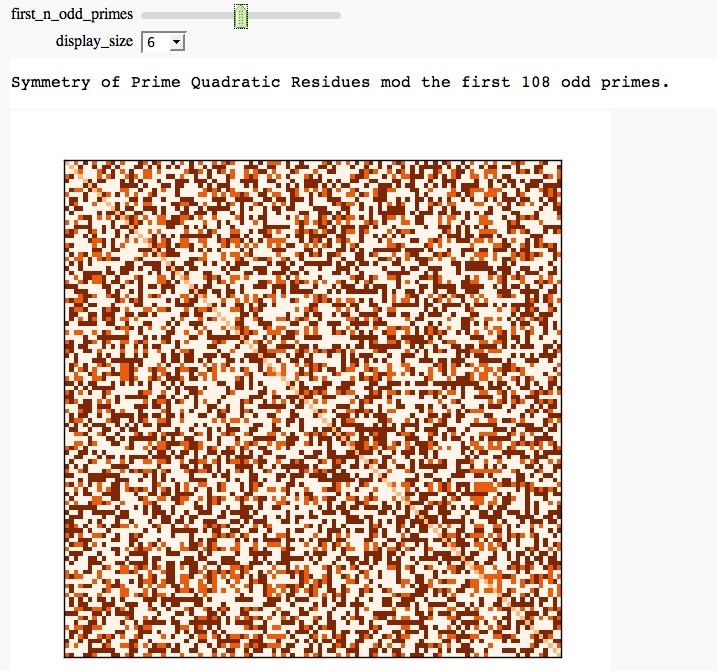
Quadratic Residue Table FIXME
by Emily Kirkman

Cubic Residue Table FIXME
by Emily Kirkman

Cyclotomic Fields
Gauss and Jacobi Sums in Complex Plane
by Emily Kirkman
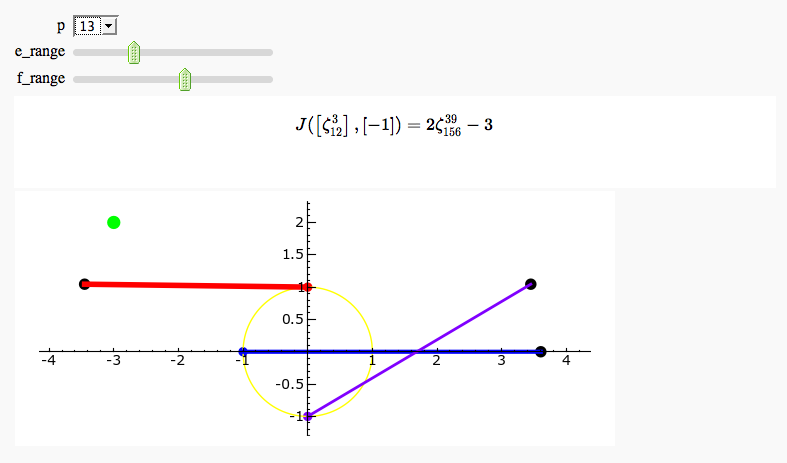
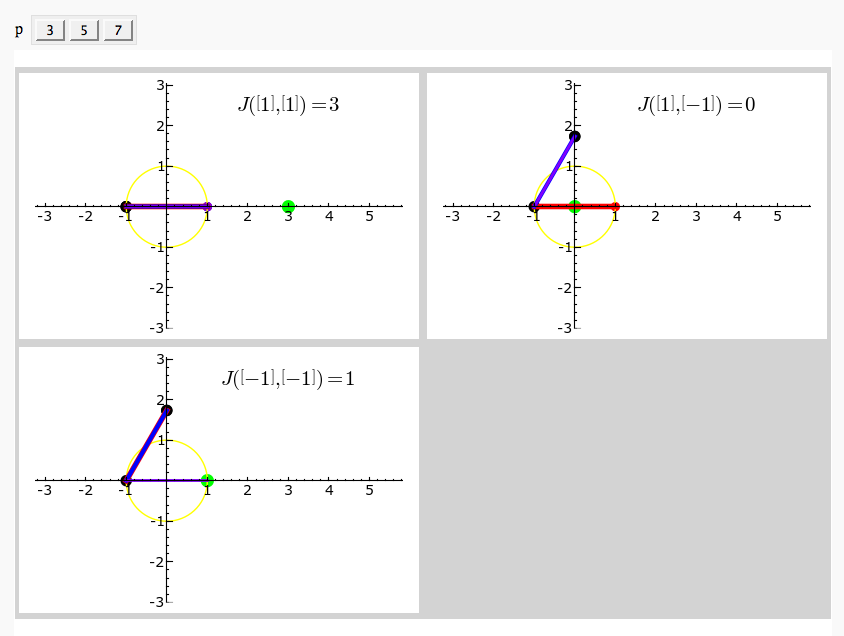
Exhaustive Jacobi Plotter
by Emily Kirkman
Elliptic Curves
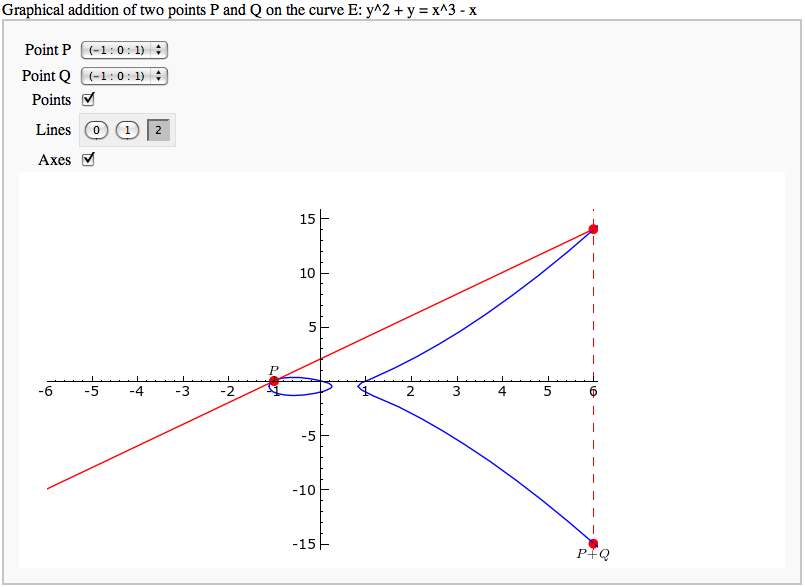
Adding points on an elliptic curve
by David Møller Hansen
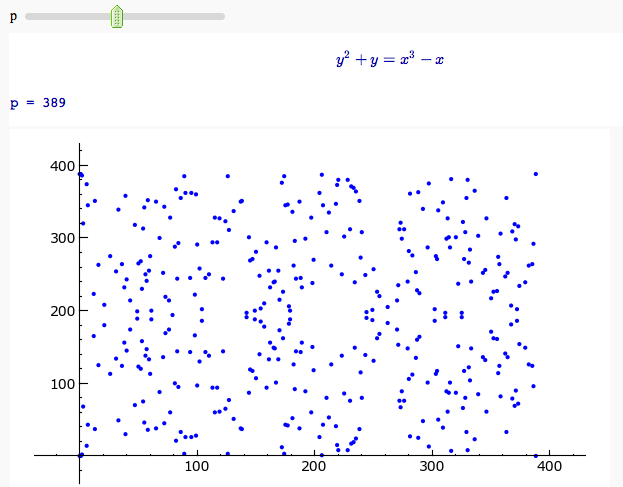
Plotting an elliptic curve over a finite field
Cryptography
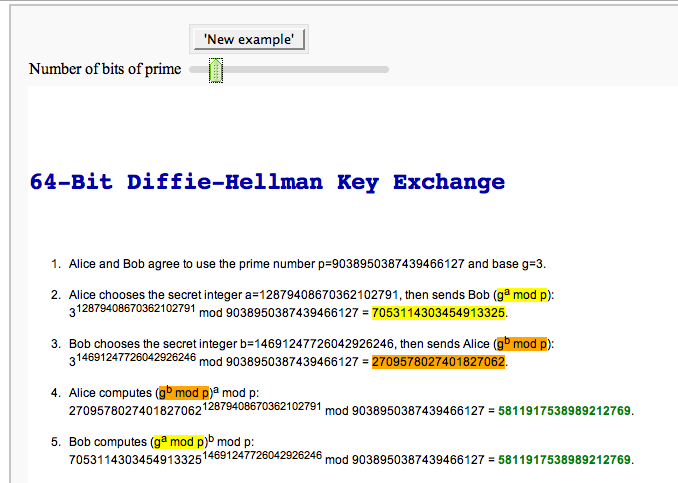
The Diffie-Hellman Key Exchange Protocol
by Timothy Clemans and William Stein
Other
Continued Fraction Plotter
by William Stein
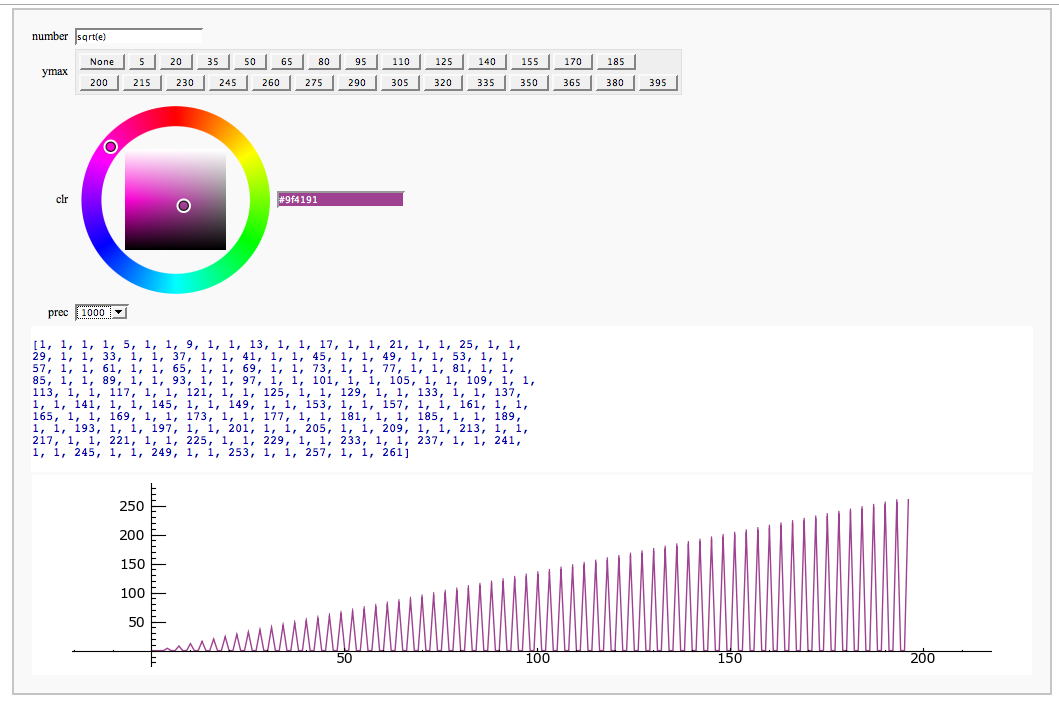
Computing Generalized Bernoulli Numbers
by William Stein (Sage-2.10.3)
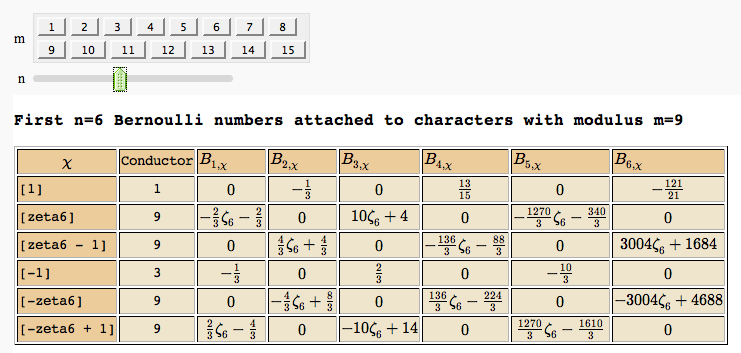
Fundamental Domains of SL_2(ZZ)
by Robert Miller
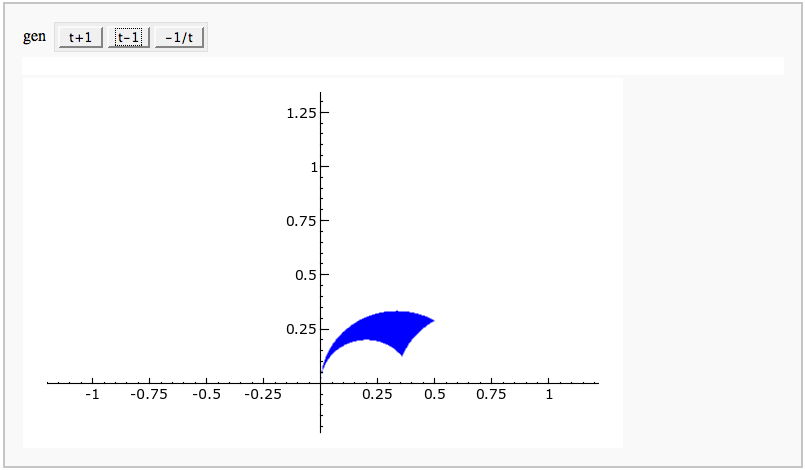
Multiple Zeta Values
by Akhilesh P.
Word to composition

Composition to Word

Dual of a Word

Computing Multiple Zeta values
Word Input

Composition Input

Shuffle product of two Words
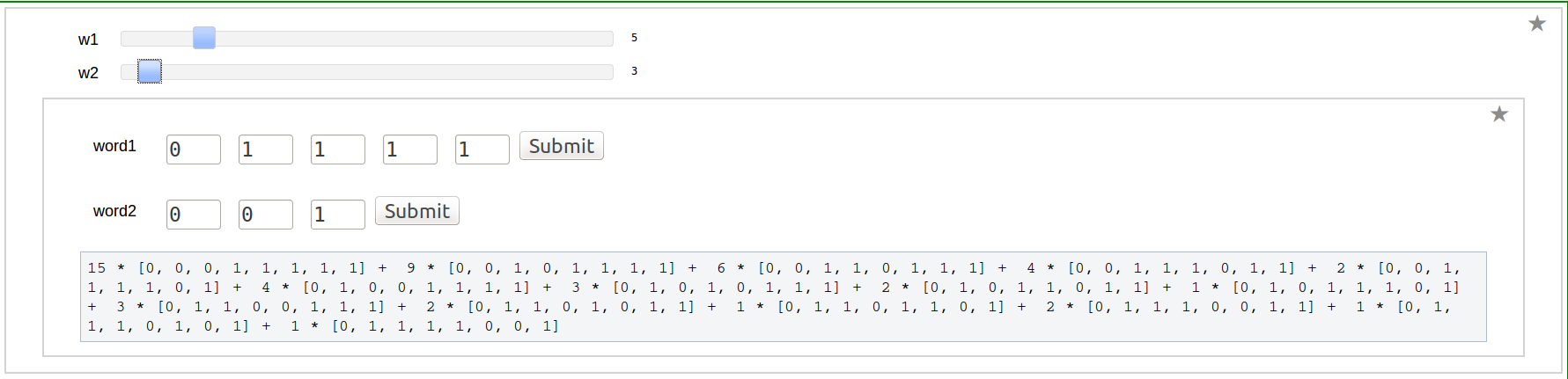
Shuffle Regularization at 0

Shuffle Regularization at 1

