|
Size: 26468
Comment:
|
Size: 29334
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 2: | Line 2: |
| goto [:interact:interact main page] [[TableOfContents]] |
goto [[interact|interact main page]] <<TableOfContents>> |
| Line 53: | Line 53: |
| attachment:factortree.png === Continued Fraction Plotter === |
{{attachment:factortree.png}} == Continued Fraction Plotter == |
| Line 63: | Line 63: |
| attachment:contfracplot.png === Illustrating the prime number thoerem === |
{{attachment:contfracplot.png}} == Illustrating the prime number theorem == |
| Line 73: | Line 73: |
| attachment:primes.png === Computing Generalized Bernoulli Numbers === |
{{attachment:primes.png}} == Computing Generalized Bernoulli Numbers == |
| Line 93: | Line 93: |
| attachment:bernoulli.png === Fundamental Domains of SL_2(ZZ) === |
{{attachment:bernoulli.png}} == Fundamental Domains of SL_2(ZZ) == |
| Line 123: | Line 123: |
| attachment:fund_domain.png === Computing modular forms === |
{{attachment:fund_domain.png}} == Computing modular forms == |
| Line 145: | Line 145: |
| attachment:modformbasis.png === Computing the cuspidal subgroup === |
{{attachment:modformbasis.png}} == Computing the cuspidal subgroup == |
| Line 158: | Line 158: |
| attachment:cuspgroup.png === A Charpoly and Hecke Operator Graph === |
{{attachment:cuspgroup.png}} == A Charpoly and Hecke Operator Graph == |
| Line 180: | Line 180: |
| attachment:heckegraph.png === Demonstrating the Diffie-Hellman Key Exchange Protocol === |
{{attachment:heckegraph.png}} == Demonstrating the Diffie-Hellman Key Exchange Protocol == |
| Line 224: | Line 224: |
| attachment:dh.png === Plotting an elliptic curve over a finite field === |
{{attachment:dh.png}} == Plotting an elliptic curve over a finite field == |
| Line 236: | Line 236: |
| attachment:ellffplot.png === Prime Spiral - Square === |
{{attachment:ellffplot.png}} == Prime Spiral - Square == |
| Line 373: | Line 373: |
| attachment:SquareSpiral.PNG === Prime Spiral - Polar === |
{{attachment:SquareSpiral.PNG}} == Prime Spiral - Polar == |
| Line 444: | Line 444: |
| attachment:PolarSpiral.PNG === Quadratic Residue Table === |
{{attachment:PolarSpiral.PNG}} == Quadratic Residue Table == |
| Line 495: | Line 495: |
| attachment:quadres.png attachment:quadresbig.png === Cubic Residue Table === |
{{attachment:quadres.png}} {{attachment:quadresbig.png}} == Cubic Residue Table == |
| Line 579: | Line 579: |
| attachment:cubres.png === Gauss and Jacobi Sums in Complex Plane === |
{{attachment:cubres.png}} == Gauss and Jacobi Sums in Complex Plane == |
| Line 659: | Line 659: |
| attachment:jacobising.png === Exhaustive Jacobi Plotter === |
{{attachment:jacobising.png}} == Exhaustive Jacobi Plotter == |
| Line 749: | Line 749: |
| attachment:jacobiexh.png | {{attachment:jacobiexh.png}} == Adding points on an elliptic curve == by David Møller Hansen {{{ def point_txt(P,name,rgbcolor): if (P.xy()[1]) < 0: r = text(name,[float(P.xy()[0]),float(P.xy()[1])-1],rgbcolor=rgbcolor) elif P.xy()[1] == 0: r = text(name,[float(P.xy()[0]),float(P.xy()[1])+1],rgbcolor=rgbcolor) else: r = text(name,[float(P.xy()[0]),float(P.xy()[1])+1],rgbcolor=rgbcolor) return r E = EllipticCurve('37a') list_of_points = E.integral_points() html("Graphical addition of two points $P$ and $Q$ on the curve $ E: %s $"%latex(E)) @interact def _(P=selector(list_of_points,label='Point P'),Q=selector(list_of_points,label='Point Q'), marked_points = checkbox(default=True,label = 'Points'), Lines = selector([0..2],nrows=1), Axes=True): curve = E.plot(rgbcolor = (0,0,1),xmin=25,xmax=25,plot_points=300) R = P + Q Rneg = -R l1 = line_from_curve_points(E,P,Q) l2 = line_from_curve_points(E,R,Rneg,style='--') p1 = plot(P,rgbcolor=(1,0,0),pointsize=40) p2 = plot(Q,rgbcolor=(1,0,0),pointsize=40) p3 = plot(R,rgbcolor=(1,0,0),pointsize=40) p4 = plot(Rneg,rgbcolor=(1,0,0),pointsize=40) textp1 = point_txt(P,"$P$",rgbcolor=(0,0,0)) textp2 = point_txt(Q,"$Q$",rgbcolor=(0,0,0)) textp3 = point_txt(R,"$P+Q$",rgbcolor=(0,0,0)) if Lines==0: g=curve elif Lines ==1: g=curve+l1 elif Lines == 2: g=curve+l1+l2 if marked_points: g=g+p1+p2+p3+p4 if P != Q: g=g+textp1+textp2+textp3 else: g=g+textp1+textp3 g.axes_range(xmin=-5,xmax=5,ymin=-13,ymax=13) show(g,axes = Axes) def line_from_curve_points(E,P,Q,style='-',rgb=(1,0,0),length=25): """ P,Q two points on an elliptic curve. Output is a graphic representation of the straight line intersecting with P,Q. """ # The function tangent to P=Q on E if P == Q: if P[2]==0: return line([(1,-length),(1,length)],linestyle=style,rgbcolor=rgb) else: # Compute slope of the curve E in P l=-(3*P[0]^2 + 2*E.a2()*P[0] + E.a4() - E.a1()*P[1])/((-2)*P[1] - E.a1()*P[0] - E.a3()) f(x) = l * (x - P[0]) + P[1] return plot(f(x),-length,length,linestyle=style,rgbcolor=rgb) # Trivial case of P != R where P=O or R=O then we get the vertical line from the other point elif P[2] == 0: return line([(Q[0],-length),(Q[0],length)],linestyle=style,rgbcolor=rgb) elif Q[2] == 0: return line([(P[0],-length),(P[0],length)],linestyle=style,rgbcolor=rgb) # Non trivial case where P != R else: # Case where x_1 = x_2 return vertical line evaluated in Q if P[0] == Q[0]: return line([(P[0],-length),(P[0],length)],linestyle=style,rgbcolor=rgb) #Case where x_1 != x_2 return line trough P,R evaluated in Q" l=(Q[1]-P[1])/(Q[0]-P[0]) f(x) = l * (x - P[0]) + P[1] return plot(f(x),-length,length,linestyle=style,rgbcolor=rgb) }}} |
Sage Interactions - Number Theory
goto interact main page
Contents
-
Sage Interactions - Number Theory
- Factor Trees
- Continued Fraction Plotter
- Illustrating the prime number theorem
- Computing Generalized Bernoulli Numbers
- Fundamental Domains of SL_2(ZZ)
- Computing modular forms
- Computing the cuspidal subgroup
- A Charpoly and Hecke Operator Graph
- Demonstrating the Diffie-Hellman Key Exchange Protocol
- Plotting an elliptic curve over a finite field
- Prime Spiral - Square
- Prime Spiral - Polar
- Quadratic Residue Table
- Cubic Residue Table
- Gauss and Jacobi Sums in Complex Plane
- Exhaustive Jacobi Plotter
- Adding points on an elliptic curve
Factor Trees
by William Stein
import random
def ftree(rows, v, i, F):
if len(v) > 0: # add a row to g at the ith level.
rows.append(v)
w = []
for i in range(len(v)):
k, _, _ = v[i]
if k is None or is_prime(k):
w.append((None,None,None))
else:
d = random.choice(divisors(k)[1:-1])
w.append((d,k,i))
e = k//d
if e == 1:
w.append((None,None))
else:
w.append((e,k,i))
if len(w) > len(v):
ftree(rows, w, i+1, F)
def draw_ftree(rows,font):
g = Graphics()
for i in range(len(rows)):
cur = rows[i]
for j in range(len(cur)):
e, f, k = cur[j]
if not e is None:
if is_prime(e):
c = (1,0,0)
else:
c = (0,0,.4)
g += text(str(e), (j*2-len(cur),-i), fontsize=font, rgbcolor=c)
if not k is None and not f is None:
g += line([(j*2-len(cur),-i), ((k*2)-len(rows[i-1]),-i+1)],
alpha=0.5)
return g
@interact
def factor_tree(n=100, font=(10, (8..20)), redraw=['Redraw']):
n = Integer(n)
rows = []
v = [(n,None,0)]
ftree(rows, v, 0, factor(n))
show(draw_ftree(rows, font), axes=False)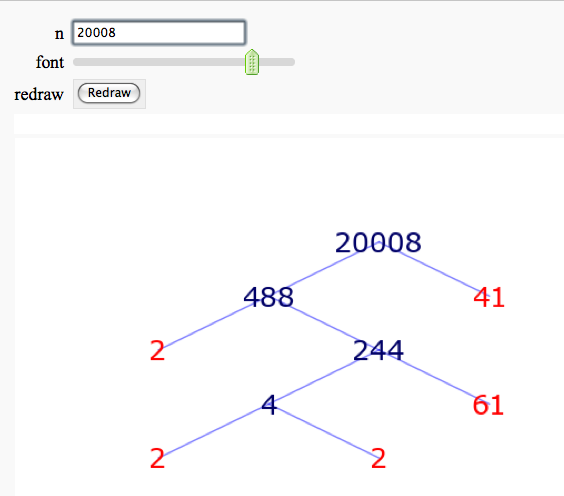
Continued Fraction Plotter
by William Stein
@interact
def _(number=e, ymax=selector([None,5,20,..,400],nrows=2), clr=Color('purple'), prec=[500,1000,..,5000]):
c = list(continued_fraction(RealField(prec)(number))); print c
show(line([(i,z) for i, z in enumerate(c)],rgbcolor=clr),ymax=ymax,figsize=[10,2])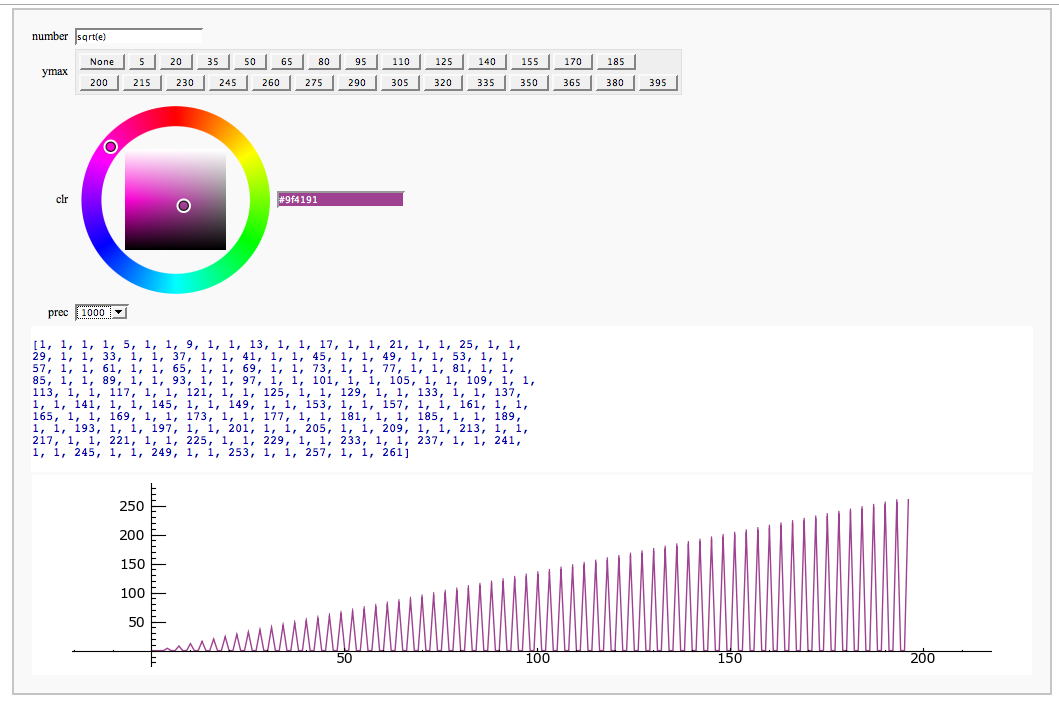
Illustrating the prime number theorem
by William Stein
@interact
def _(N=(100,(2..2000))):
html("<font color='red'>$\pi(x)$</font> and <font color='blue'>$x/(\log(x)-1)$</font> for $x < %s$"%N)
show(plot(prime_pi, 0, N, rgbcolor='red') + plot(x/(log(x)-1), 5, N, rgbcolor='blue'))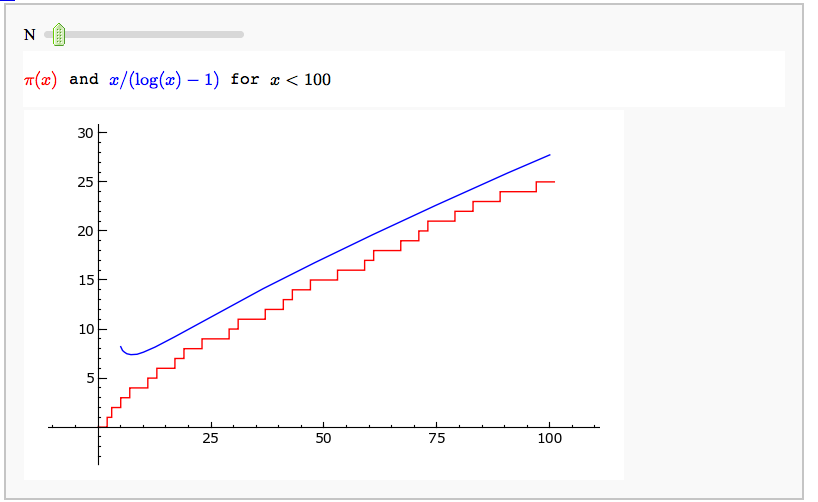
Computing Generalized Bernoulli Numbers
by William Stein (Sage-2.10.3)
@interact
def _(m=selector([1..15],nrows=2), n=(7,(3..10))):
G = DirichletGroup(m)
s = "<h3>First n=%s Bernoulli numbers attached to characters with modulus m=%s</h3>"%(n,m)
s += '<table border=1>'
s += '<tr bgcolor="#edcc9c"><td align=center>$\\chi$</td><td>Conductor</td>' + \
''.join('<td>$B_{%s,\chi}$</td>'%k for k in [1..n]) + '</tr>'
for eps in G.list():
v = ''.join(['<td align=center bgcolor="#efe5cd">$%s$</td>'%latex(eps.bernoulli(k)) for k in [1..n]])
s += '<tr><td bgcolor="#edcc9c">%s</td><td bgcolor="#efe5cd" align=center>%s</td>%s</tr>\n'%(
eps, eps.conductor(), v)
s += '</table>'
html(s)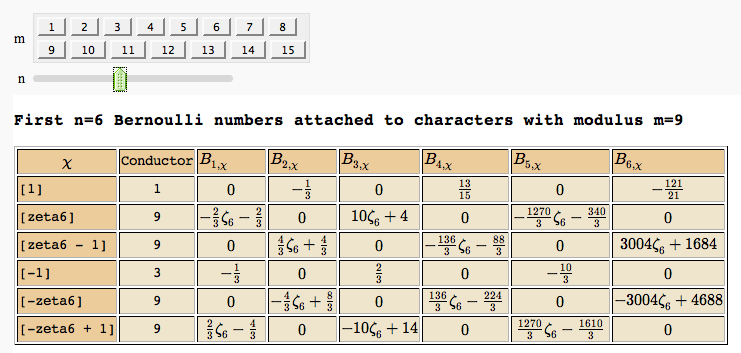
Fundamental Domains of SL_2(ZZ)
by Robert Miller
L = [[-0.5, 2.0^(x/100.0) - 1 + sqrt(3.0)/2] for x in xrange(1000, -1, -1)]
R = [[0.5, 2.0^(x/100.0) - 1 + sqrt(3.0)/2] for x in xrange(1000)]
xes = [x/1000.0 for x in xrange(-500,501,1)]
M = [[x,abs(sqrt(x^2-1))] for x in xes]
fundamental_domain = L+M+R
fundamental_domain = [[x-1,y] for x,y in fundamental_domain]
@interact
def _(gen = selector(['t+1', 't-1', '-1/t'], nrows=1)):
global fundamental_domain
if gen == 't+1':
fundamental_domain = [[x+1,y] for x,y in fundamental_domain]
elif gen == 't-1':
fundamental_domain = [[x-1,y] for x,y in fundamental_domain]
elif gen == '-1/t':
new_dom = []
for x,y in fundamental_domain:
sq_mod = x^2 + y^2
new_dom.append([(-1)*x/sq_mod, y/sq_mod])
fundamental_domain = new_dom
P = polygon(fundamental_domain)
P.ymax(1.2); P.ymin(-0.1)
P.show()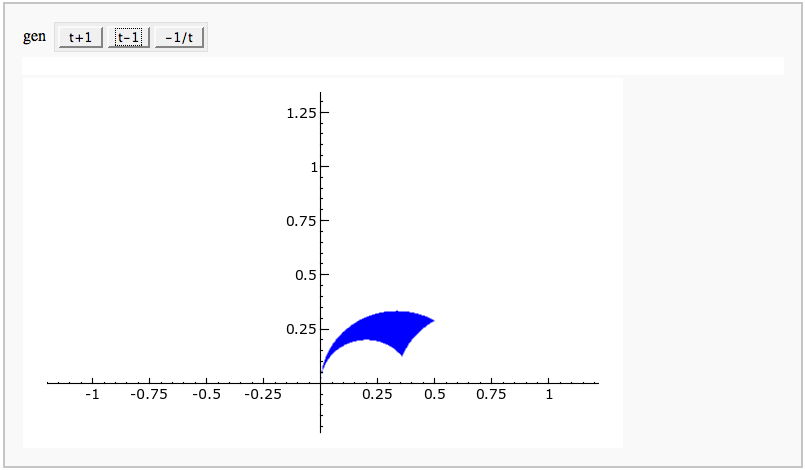
Computing modular forms
by William Stein
j = 0
@interact
def _(N=[1..100], k=selector([2,4,..,12],nrows=1), prec=(3..40),
group=[(Gamma0, 'Gamma0'), (Gamma1, 'Gamma1')]):
M = CuspForms(group(N),k)
print j; global j; j += 1
print M; print '\n'*3
print "Computing basis...\n\n"
if M.dimension() == 0:
print "Space has dimension 0"
else:
prec = max(prec, M.dimension()+1)
for f in M.basis():
view(f.q_expansion(prec))
print "\n\n\nDone computing basis."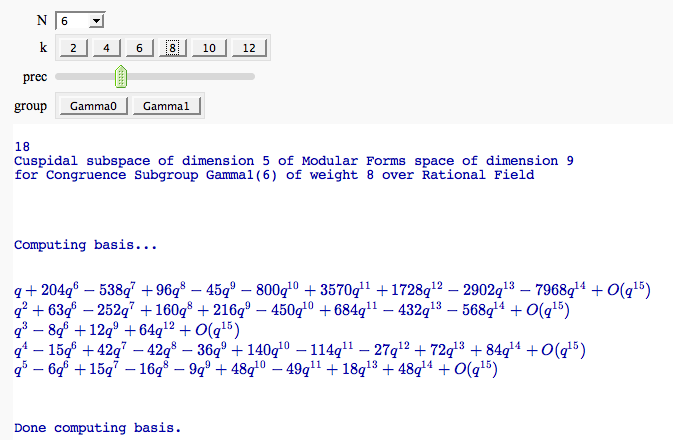
Computing the cuspidal subgroup
by William Stein
html('<h1>Cuspidal Subgroups of Modular Jacobians J0(N)</h1>')
@interact
def _(N=selector([1..8*13], ncols=8, width=10, default=10)):
A = J0(N)
print A.cuspidal_subgroup()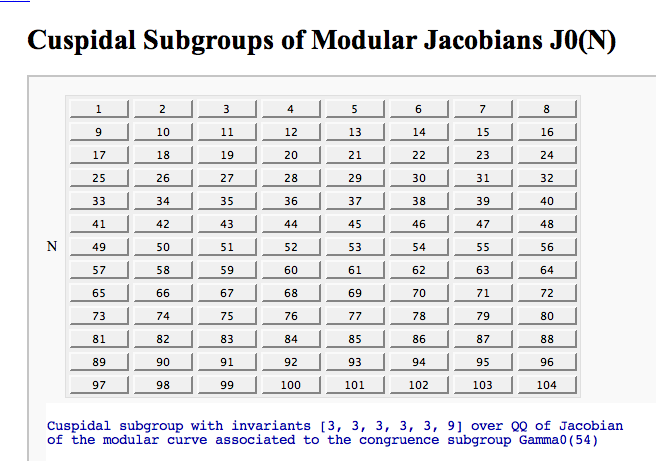
A Charpoly and Hecke Operator Graph
by William Stein
# Note -- in Sage-2.10.3; multiedges are missing in plots; loops are missing in 3d plots
@interact
def f(N = prime_range(11,400),
p = selector(prime_range(2,12),nrows=1),
three_d = ("Three Dimensional", False)):
S = SupersingularModule(N)
T = S.hecke_matrix(p)
G = Graph(T, multiedges=True, loops=not three_d)
html("<h1>Charpoly and Hecke Graph: Level %s, T_%s</h1>"%(N,p))
show(T.charpoly().factor())
if three_d:
show(G.plot3d(), aspect_ratio=[1,1,1])
else:
show(G.plot(),figsize=7)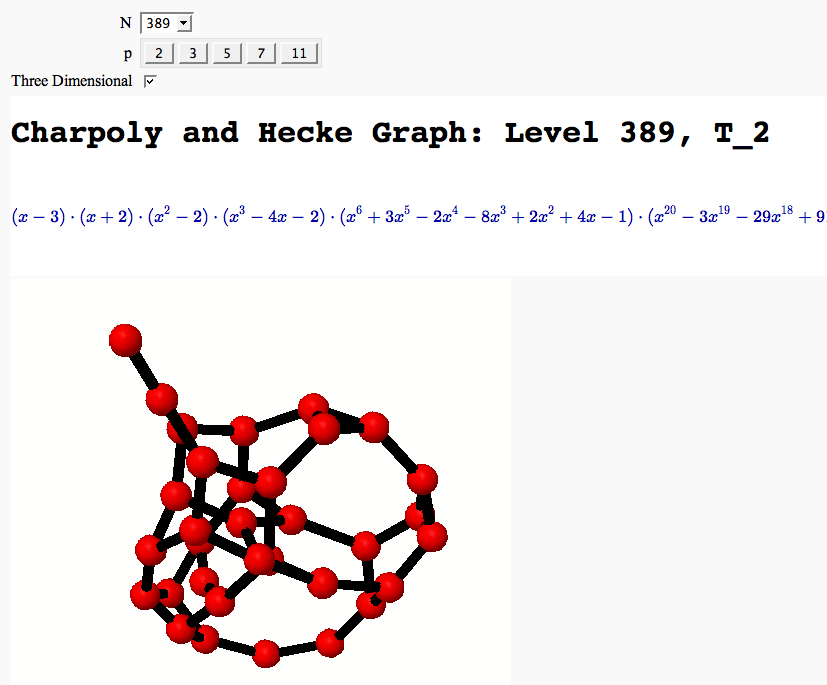
Demonstrating the Diffie-Hellman Key Exchange Protocol
by Timothy Clemans (refereed by William Stein)
@interact
def diffie_hellman(button=selector(["New example"],label='',buttons=True),
bits=("Number of bits of prime", (8,12,..512))):
maxp = 2^bits
p = random_prime(maxp)
k = GF(p)
if bits>100:
g = k(2)
else:
g = k.multiplicative_generator()
a = ZZ.random_element(10, maxp)
b = ZZ.random_element(10, maxp)
print """
<html>
<style>
.gamodp {
background:yellow
}
.gbmodp {
background:orange
}
.dhsame {
color:green;
font-weight:bold
}
</style>
<h2>%s-Bit Diffie-Hellman Key Exchange</h2>
<ol style="color:#000;font:12px Arial, Helvetica, sans-serif">
<li>Alice and Bob agree to use the prime number p=%s and base g=%s.</li>
<li>Alice chooses the secret integer a=%s, then sends Bob (<span class="gamodp">g<sup>a</sup> mod p</span>):<br/>%s<sup>%s</sup> mod %s = <span class="gamodp">%s</span>.</li>
<li>Bob chooses the secret integer b=%s, then sends Alice (<span class="gbmodp">g<sup>b</sup> mod p</span>):<br/>%s<sup>%s</sup> mod %s = <span class="gbmodp">%s</span>.</li>
<li>Alice computes (<span class="gbmodp">g<sup>b</sup> mod p</span>)<sup>a</sup> mod p:<br/>%s<sup>%s</sup> mod %s = <span class="dhsame">%s</span>.</li>
<li>Bob computes (<span class="gamodp">g<sup>a</sup> mod p</span>)<sup>b</sup> mod p:<br/>%s<sup>%s</sup> mod %s = <span class="dhsame">%s</span>.</li>
</ol></html>
""" % (bits, p, g, a, g, a, p, (g^a), b, g, b, p, (g^b), (g^b), a, p,
(g^ b)^a, g^a, b, p, (g^a)^b)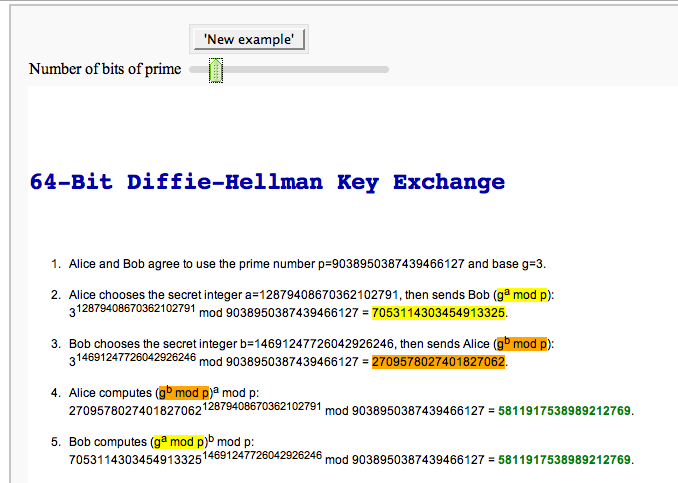
Plotting an elliptic curve over a finite field
E = EllipticCurve('37a')
@interact
def _(p=slider(prime_range(1000), default=389)):
show(E)
print "p = %s"%p
show(E.change_ring(GF(p)).plot(),xmin=0,ymin=0)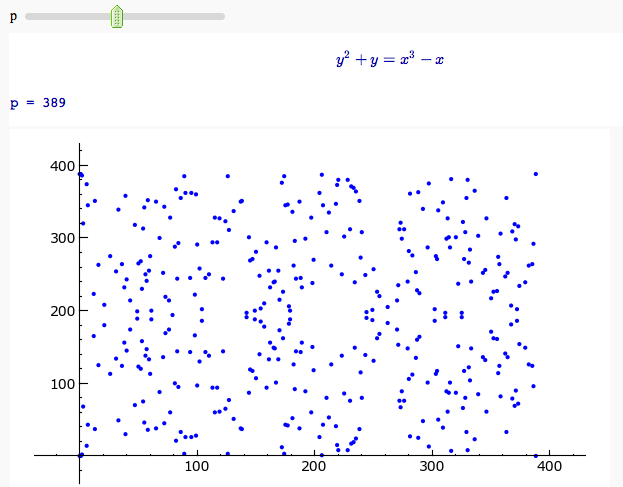
Prime Spiral - Square
by David Runde
@interact
def square_prime_spiral(start=1, end=100, size_limit = 10, show_lines=false, invert=false, x_cord=0, y_cord=0, n = 0):
"""
REFERENCES:
Alpern, Dario. "Ulam's Spiral". http://www.alpertron.com.ar/ULAM.HTM
Sacks, Robert. http://www.NumberSpiral.com
Ventrella, Jeffery. "Prime Numbers are the Holes Behind Complex Composite Patterns". http://www.divisorplot.com
Williamson, John. Number Spirals. http://www.dcs.gla.ac.uk/~jhw/spirals/index.html jhw@dcs.gla.ac.uk
Weisstein, Eric W. "Prime-Generating Polynomial." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Prime-GeneratingPolynomial.html
"""
#Takes an (x,y) coordinate (and the start of the spiral) and gives its corresponding n value
def find_n(x,y, start):
if x>0 and y>-x and y<=x: return 4*(x-1)^2 + 5*(x-1) + (start+1) + y
elif x<=0 and y>=x and y<=-x: return 4*x^2 - x + (start) -y
elif y>=0 and -y+1 <= x and y-1 >= x: return 4*y^2 -y + start -x
elif y<0 and -x >= y and y<x: return 4*(y+1)^2 -11*(y+1) + (start+7) +x
else: print 'NaN'
#Takes in an n and the start value of the spiral and gives its (x,y) coordinate
def find_xy(num, start):
num = num - start +1
bottom = floor(sqrt(num))
top = ceil(sqrt(num))
if bottom^2 < num and num<=bottom^2+bottom+1:
if bottom%2 == 0:
x=-bottom/2
y=-x-(num-bottom^2)+1
else:
x=bottom/2+1/2
y=-x + (num-bottom^2)
else:
if top%2 == 0:
y=top/2
x=-top/2+1+top^2-num
else:
y=-top/2+1/2
x=top/2 -1/2 - (top^2-num)
x = Integer(x)
y = Integer(y)
return (x,y)
if start < 1 or end <=start: print "invalid start or end value"
if n > end: print "WARNING: n is larger than the end value"
#Changes the entry of a matrix by taking the old matrix and the (x,y) coordinate (in matrix coordinates) and returns the changed matrix
def matrix_morph(M, x, y, set):
N = M.copy()
N[x-1,y] = set
M = N
return M
#These functions return an int based on where the t is located in the spiral
def SW_NE(t, x, y, start):
if -y<x: return 4*t^2 + 2*t -x+y+start
else: return 4*t^2 + 2*t +x-y+start
def NW_SE(t, x, y, start):
if x<y: return 4*t^2 -x-y+start
else: return 4*t^2 + 4*t +x+y+start
size = ceil(sqrt(end-start+1)) #Size of the matrix
num=copy(start) # Start number (might not be used)
x = ceil(size/2) #starting center x of the matrix (in matrix coordinates)
y = copy(x) #starting center y of the matrix (in matrix coordinates)
if n !=0: x_cord, y_cord = find_xy(n, start) #Overrides the user given x and y coordinates
xt = copy(x_cord)
yt = copy(y_cord)
countx=0
county=0
overcount = 1
if size <= size_limit: M = matrix(ZZ, size+1) # Allows the numbers to be seen in the smaller matricies
else: M = matrix(GF(2), size+1) # Restricts the entries to 0 or 1
main_list = set()
#print x_cord, y_cord
if show_lines:
for t in [(-size-1)..size+1]:
m= SW_NE(t, xt, yt, start)
if m.is_pseudoprime(): main_list.add(m)
m= NW_SE(t, xt, yt, start)
if m.is_pseudoprime(): main_list.add(m)
else: main_list = set(prime_range(end))
#This for loop changes the matrix by spiraling out from the center and changing each entry as it goes. It is faster than the find_xy function above.
for num in [start..end]:
#print x, "=x y=", y, " num =", num
if countx < overcount:
if overcount % 2 == 1: x+=1
else: x-=1
countx += 1
elif county < overcount:
if overcount % 2 == 1: y+=1
else: y-=1
county += 1
else:
overcount += 1
countx=2
county=0
if overcount % 2 == 1: x+=1
else: x-=1
if not invert and num in main_list:
if size <= size_limit: M = matrix_morph(M, x, y, num)
else: M = matrix_morph(M, x, y, 1)
elif invert and num not in main_list: #This does the opposite of the above if statement by changing the matrix only when a number is not in the list of allowable primes
if size <= size_limit: M = matrix_morph(M, x, y, num)
else: M = matrix_morph(M, x, y, 1)
if n != 0:
print '(to go from x,y coords to an n, reset by setting n=0)'
(x_cord, y_cord) = find_xy(n, start)
#print 'if n =', n, 'then (x,y) =', (x_cord, y_cord)
print '(x,y) =', (x_cord, y_cord), '<=> n =', find_n(x_cord, y_cord, start)
print ' '
print "SW/NE line"
if -y_cord<x_cord: print '4*t^2 + 2*t +', -x_cord+y_cord+start
else: print '4*t^2 + 2*t +', +x_cord-y_cord+start
print "NW/SE line"
if x_cord<y_cord: print '4*t^2 +', -x_cord-y_cord+start
else: print '4*t^2 + 4*t +', +x_cord+y_cord+start
if size <= size_limit: show(M) #Displays the matrix with integer entries
else:
M.visualize_structure() # Displays the final resulting matrix as a series of pixels (1 <=> pixel on)
#matrix_plot(M)
Prime Spiral - Polar
by David Runde
@interact
def polar_prime_spiral(start=1, end=2000, show_factors = false, highlight_primes = false, show_curves=true, n = 0):
#For more information about the factors in the spiral, visit http://www.dcs.gla.ac.uk/~jhw/spirals/index.html by John Williamson.
if start < 1 or end <=start: print "invalid start or end value"
if n > end: print "WARNING: n is greater than end value"
def f(n):
return (sqrt(n)*cos(2*pi*sqrt(n)), sqrt(n)*sin(2*pi*sqrt(n)))
list =[]
list2=[]
if show_factors == false:
for i in [start..end]:
if i.is_pseudoprime(): list.append(f(i-start+1)) #Primes list
else: list2.append(f(i-start+1)) #Composites list
P = points(list)
R = points(list2, alpha = .1) #Faded Composites
else:
for i in [start..end]:
list.append(disk((f(i-start+1)),0.05*pow(2,len(factor(i))-1), (0,2*pi))) #resizes each of the dots depending of the number of factors of each number
if i.is_pseudoprime() and highlight_primes: list2.append(f(i-start+1))
P = plot(list)
p_size = 5 #the orange dot size of the prime markers
if not highlight_primes: list2 = [(f(n-start+1))]
R=points(list2, hue = .1, pointsize = p_size)
if n > 0:
print 'n =', factor(n)
p = 1
#The X which marks the given n
W1 = disk((f(n-start+1)), p, (pi/6, 2*pi/6))
W2 = disk((f(n-start+1)), p, (4*pi/6, 5*pi/6))
W3 = disk((f(n-start+1)), p, (7*pi/6, 8*pi/6))
W4 = disk((f(n-start+1)), p, (10*pi/6, 11*pi/6))
Q = plot(W1+W2+W3+W4, alpha = .1)
n=n-start+1 #offsets the n for different start values to ensure accurate plotting
if show_curves:
begin_curve = 0
t = var('t')
a=1
b=0
if n > (floor(sqrt(n)))^2 and n <= (floor(sqrt(n)))^2 + floor(sqrt(n)):
c = -((floor(sqrt(n)))^2 - n)
c2= -((floor(sqrt(n)))^2 + floor(sqrt(n)) - n)
else:
c = -((ceil(sqrt(n)))^2 - n)
c2= -((floor(sqrt(n)))^2 + floor(sqrt(n)) - n)
print 'Pink Curve: n^2 +', c
print 'Green Curve: n^2 + n +', c2
def g(m): return (a*m^2+b*m+c);
def r(m) : return sqrt(g(m))
def theta(m) : return r(m)- m*sqrt(a)
S1 = parametric_plot(((r(t))*cos(2*pi*(theta(t))),(r(t))*sin(2*pi*(theta(t)))), begin_curve, ceil(sqrt(end-start)), rgbcolor=hue(0.8), thickness = .2) #Pink Line
b=1
c= c2;
S2 = parametric_plot(((r(t))*cos(2*pi*(theta(t))),(r(t))*sin(2*pi*(theta(t)))), begin_curve, ceil(sqrt(end-start)), rgbcolor=hue(0.6), thickness = .2) #Green Line
show(R+P+S1+S2+Q, aspect_ratio = 1, axes = false)
else: show(R+P+Q, aspect_ratio = 1, axes = false)
else: show(R+P, aspect_ratio = 1, axes = false)
Quadratic Residue Table
by Emily Kirkman
from numpy import array as narray
@interact
def quad_res_plot(first_n_odd_primes = (20,200),display_size=[7..15]):
# Compute numpy matrix of legendre symbols
r = int(first_n_odd_primes)
np = [nth_prime(i+2) for i in range(r)]
leg = [[legendre_symbol(np[i], np[j]) for i in range(r)] for j in range(r)]
na = narray(leg)
for i in range(r):
for j in range(r):
if na[i][j] == 1 and Mod((np[i]-1)*(np[j]-1)//4,2) == 0:
na[i][j] = 2
m = matrix(na)
# Define plot structure
MP = matrix_plot(m, cmap='Oranges')
for i in range(r):
if np[-1] < 100:
MP += text('%d'%nth_prime(i+2),(-.75,r-i-.5), rgbcolor='black')
MP += text('%d'%nth_prime(i+2), (i+.5,r+.5), rgbcolor='black')
if len(np) < 75:
MP += line([(0,i),(r,i)], rgbcolor='black')
MP += line([(i,0),(i,r)], rgbcolor='black')
if np[-1] < 100:
for i in range(r): # rows
for j in range(r): # cols
if m[j][i] == 0:
MP += text('0',(i+.5,r-j-.5),rgbcolor='black')
elif m[j][i] == -1:
MP += text('N',(i+.5,r-j-.5),rgbcolor='black')
elif m[j][i] == 1:
MP += text('A',(i+.5,r-j-.5),rgbcolor='black')
elif m[j][i] == 2:
MP += text('S',(i+.5,r-j-.5),rgbcolor='black')
MP += line([(0,r),(r,r)], rgbcolor='black')
MP += line([(r,0),(r,r)], rgbcolor='black')
MP += line([(0,0),(r,0)], rgbcolor='black')
MP += line([(0,0),(0,r)], rgbcolor='black')
if len(np) < 75:
MP += text('q',(r/2,r+2), rgbcolor='black', fontsize=15)
MP += text('p',(-2.5,r/2), rgbcolor='black', fontsize=15)
MP.show(axes=False, ymax=r, figsize=[display_size,display_size])
html('Symmetry of Prime Quadratic Residues mod the first %d odd primes.'%r)
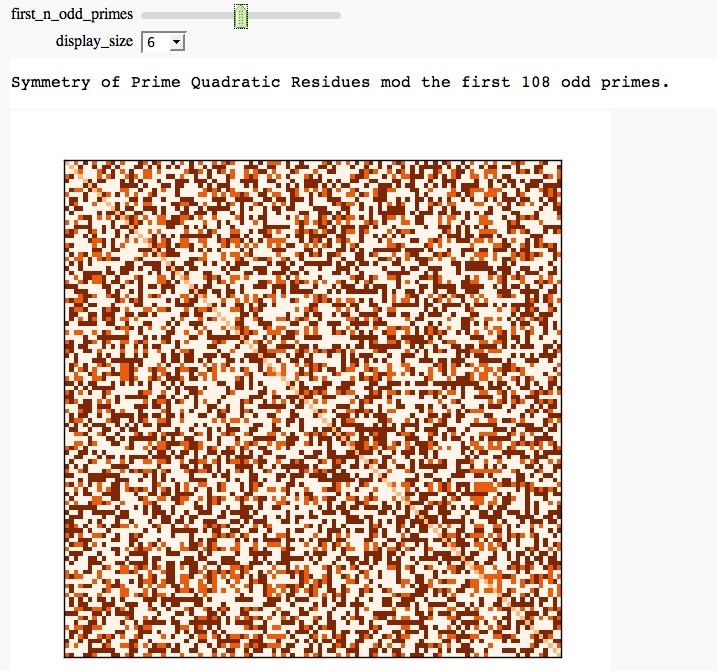
Cubic Residue Table
by Emily Kirkman
def power_residue_symbol(alpha, p, m):
if p.divides(alpha): return 0
if not p.is_prime():
return prod(power_residue_symbol(alpha,ell,m)^e
for ell, e in p.factor())
F = p.residue_field()
N = p.norm()
r = F(alpha)^((N-1)/m)
k = p.number_field()
for kr in k.roots_of_unity():
if r == F(kr):
return kr
def cubic_is_primary(n):
g = n.gens_reduced()[0]
a,b = g.polynomial().coefficients()
if Mod(a,3)!=0 and Mod(b,3)==0:
return True
else:
return False
from numpy import array as narray
@interact
def cubic_sym(n=(10..35),display_size=[7..15]):
# Compute numpy matrix of primary cubic residue symbols
r = n
m=3
D.<w> = NumberField(x^2+x+1)
it = D.primes_of_degree_one_iter()
pp = []
while len(pp) < r:
k = it.next()
if cubic_is_primary(k):
pp.append(k)
n = narray([ [ power_residue_symbol(pp[i].gens_reduced()[0], pp[j], m) \
for i in range(r) ] for j in range(r) ])
# Convert to integer matrix for gradient colors
for i in range(r):
for j in range(r):
if n[i][j] == w:
n[i][j] = int(-1)
elif n[i][j] == w^2:
n[i][j] = int(-2)
elif n[i][j] == 1:
n[i][j] = int(1)
m = matrix(n)
# Define plot structure
MP = matrix_plot(m,cmap="Blues")
for i in range(r):
MP += line([(0,i),(r,i)], rgbcolor='black')
MP += line([(i,0),(i,r)], rgbcolor='black')
for j in range(r):
if m[i][j] == -2:
MP += text('$\omega^2$',(i+.5,r-j-.5),rgbcolor='black')
if m[i][j] == -1:
MP += text('$\omega $',(i+.5,r-j-.5),rgbcolor='black')
if m[i][j] == 0:
MP += text('0',(i+.5,r-j-.5),rgbcolor='black')
if m[i][j] == 1:
MP += text('R',(i+.5,r-j-.5),rgbcolor='white')
MP += line([(0,r),(r,r)], rgbcolor='black')
MP += line([(r,0),(r,r)], rgbcolor='black')
MP += line([(0,0),(r,0)], rgbcolor='black')
MP += line([(0,0),(0,r)], rgbcolor='black')
MP += text('$ \pi_1$',(r/2,r+2), rgbcolor='black', fontsize=25)
MP += text('$ \pi_2$',(-2.5,r/2), rgbcolor='black', fontsize=25)
html('Symmetry of Primary Cubic Residues mod ' \
+ '%d primary primes in $ \mathbf Z[\omega]$.'%r)
MP.show(axes=False, figsize=[display_size,display_size])
Gauss and Jacobi Sums in Complex Plane
by Emily Kirkman
def jacobi_sum(e,f):
# If they are both trivial, return p
if e.is_trivial() and f.is_trivial():
return (e.parent()).order() + 1
# If they are inverses of each other, return -e(-1)
g = e*f
if g.is_trivial():
return -e(-1)
# If both are nontrivial, apply mult. formula:
elif not e.is_trivial() and not f.is_trivial():
return e.gauss_sum()*f.gauss_sum()/g.gauss_sum()
# If exactly one is trivial, return 0
else:
return 0
def latex2(e):
return latex(list(e.values_on_gens()))
def jacobi_plot(p, e_index, f_index, with_text=True):
# Set values
G = DirichletGroup(p)
e = G[e_index]
f = G[f_index]
ef = e*f
js = jacobi_sum(e,f)
e_gs = e.gauss_sum()
f_gs = f.gauss_sum()
ef_gs = (e*f).gauss_sum()
# Compute complex coordinates
f_pt = list(f.values_on_gens()[0].complex_embedding())
e_pt = list(e.values_on_gens()[0].complex_embedding())
ef_pt = list(ef.values_on_gens()[0].complex_embedding())
f_gs_pt = list(f_gs.complex_embedding())
e_gs_pt = list(e_gs.complex_embedding())
ef_gs_pt = list(ef_gs.complex_embedding())
try:
js = int(js)
js_pt = [CC(js)]
except:
js_pt = list(js.complex_embedding())
# Define plot structure
S = circle((0,0),1,rgbcolor='yellow') \
+ line([e_pt,e_gs_pt], rgbcolor='red', thickness=4) \
+ line([f_pt,f_gs_pt], rgbcolor='blue', thickness=3) \
+ line([ef_pt,ef_gs_pt], rgbcolor='purple',thickness=2) \
+ point(e_pt,pointsize=50, rgbcolor='red') \
+ point(f_pt,pointsize=50, rgbcolor='blue') \
+ point(ef_pt,pointsize=50,rgbcolor='purple') \
+ point(f_gs_pt,pointsize=75, rgbcolor='black') \
+ point(e_gs_pt,pointsize=75, rgbcolor='black') \
+ point(ef_gs_pt,pointsize=75, rgbcolor='black') \
+ point(js_pt,pointsize=100,rgbcolor='green')
if with_text:
S += text('$J(%s,%s) = %s$'%(latex2(e),latex2(f),latex(js)), \
(3,2.5),fontsize=15, rgbcolor='black')
else:
html('$$J(%s,%s) = %s$$'%(latex2(e),latex2(f),latex(js)))
return S
@interact
def single_jacobi_plot(p=prime_range(3,100), e_range=(0..100), f_range=(0..100)):
e_index = floor((p-2)*e_range/100)
f_index = floor((p-2)*f_range/100)
S = jacobi_plot(p,e_index,f_index,with_text=False)
S.show(aspect_ratio=1)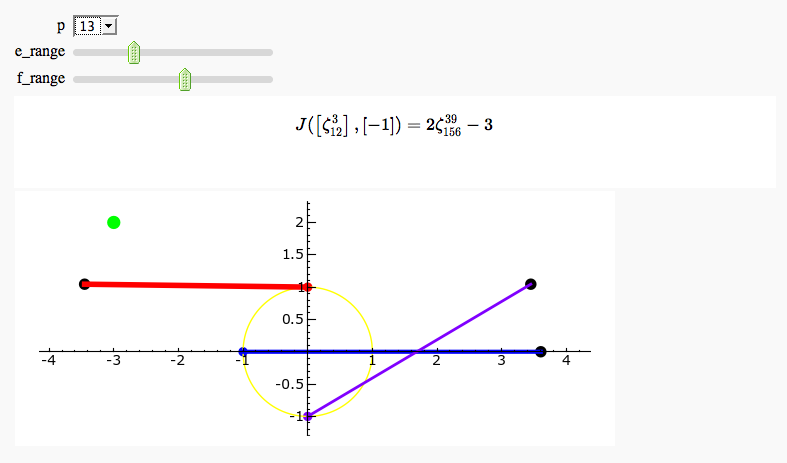
Exhaustive Jacobi Plotter
by Emily Kirkman
def jacobi_sum(e,f):
# If they are both trivial, return p
if e.is_trivial() and f.is_trivial():
return (e.parent()).order() + 1
# If they are inverses of each other, return -e(-1)
g = e*f
if g.is_trivial():
return -e(-1)
# If both are nontrivial, apply mult. formula:
elif not e.is_trivial() and not f.is_trivial():
return e.gauss_sum()*f.gauss_sum()/g.gauss_sum()
# If exactly one is trivial, return 0
else:
return 0
def latex2(e):
return latex(list(e.values_on_gens()))
def jacobi_plot(p, e_index, f_index, with_text=True):
# Set values
G = DirichletGroup(p)
e = G[e_index]
f = G[f_index]
ef = e*f
js = jacobi_sum(e,f)
e_gs = e.gauss_sum()
f_gs = f.gauss_sum()
ef_gs = (e*f).gauss_sum()
# Compute complex coordinates
f_pt = list(f.values_on_gens()[0].complex_embedding())
e_pt = list(e.values_on_gens()[0].complex_embedding())
ef_pt = list(ef.values_on_gens()[0].complex_embedding())
f_gs_pt = list(f_gs.complex_embedding())
e_gs_pt = list(e_gs.complex_embedding())
ef_gs_pt = list(ef_gs.complex_embedding())
try:
js = int(js)
js_pt = [CC(js)]
except:
js_pt = list(js.complex_embedding())
# Define plot structure
S = circle((0,0),1,rgbcolor='yellow') \
+ line([e_pt,e_gs_pt], rgbcolor='red', thickness=4) \
+ line([f_pt,f_gs_pt], rgbcolor='blue', thickness=3) \
+ line([ef_pt,ef_gs_pt], rgbcolor='purple',thickness=2) \
+ point(e_pt,pointsize=50, rgbcolor='red') \
+ point(f_pt,pointsize=50, rgbcolor='blue') \
+ point(ef_pt,pointsize=50,rgbcolor='purple') \
+ point(f_gs_pt,pointsize=75, rgbcolor='black') \
+ point(e_gs_pt,pointsize=75, rgbcolor='black') \
+ point(ef_gs_pt,pointsize=75, rgbcolor='black') \
+ point(js_pt,pointsize=100,rgbcolor='green')
if with_text:
S += text('$J(%s,%s) = %s$'%(latex2(e),latex2(f),latex(js)), \
(3,2.5),fontsize=15, rgbcolor='black')
else:
html('$$J(%s,%s) = %s$$'%(latex2(e),latex2(f),latex(js)))
return S
@interact
def exhaustive_jacobi_plot(p=prime_range(3,8)):
ga = [jacobi_plot(p,i,j) for i in range(p-1) for j in range(p-1)[i:]]
for i in range(len(ga)):
ga[i].save('j%d.PNG'%i,figsize=4,aspect_ratio=1, \
xmin=-2.5,xmax=5, ymin=-2.5, ymax=2.5)
# Since p is odd, will have n = p-1 even. So 1+2+...+n = (n/2)*(n+1).
# We divide this by rows of 2.
rows = ceil(p*(p-1)/4)
html('<table bgcolor=lightgrey cellpadding=2>')
for i in range(rows):
html('<tr><td align="center"><img src="cell://j%d.PNG"></td>'%(2*i))
html('<td align="center"><img src="cell://j%d.PNG"></td></tr>'%(2*i+1))
html('</table>')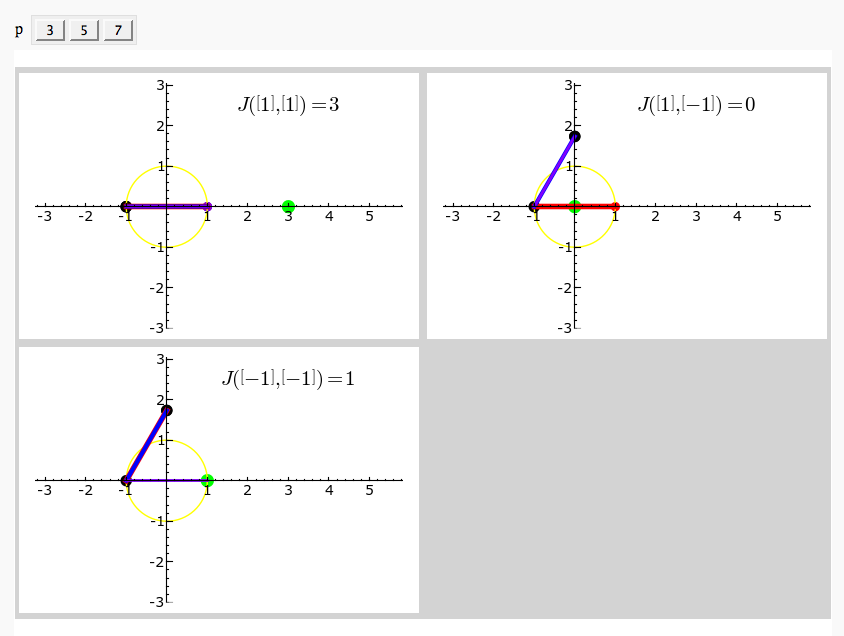
Adding points on an elliptic curve
by David Møller Hansen
def point_txt(P,name,rgbcolor):
if (P.xy()[1]) < 0:
r = text(name,[float(P.xy()[0]),float(P.xy()[1])-1],rgbcolor=rgbcolor)
elif P.xy()[1] == 0:
r = text(name,[float(P.xy()[0]),float(P.xy()[1])+1],rgbcolor=rgbcolor)
else:
r = text(name,[float(P.xy()[0]),float(P.xy()[1])+1],rgbcolor=rgbcolor)
return r
E = EllipticCurve('37a')
list_of_points = E.integral_points()
html("Graphical addition of two points $P$ and $Q$ on the curve $ E: %s $"%latex(E))
@interact
def _(P=selector(list_of_points,label='Point P'),Q=selector(list_of_points,label='Point Q'), marked_points = checkbox(default=True,label = 'Points'), Lines = selector([0..2],nrows=1), Axes=True):
curve = E.plot(rgbcolor = (0,0,1),xmin=25,xmax=25,plot_points=300)
R = P + Q
Rneg = -R
l1 = line_from_curve_points(E,P,Q)
l2 = line_from_curve_points(E,R,Rneg,style='--')
p1 = plot(P,rgbcolor=(1,0,0),pointsize=40)
p2 = plot(Q,rgbcolor=(1,0,0),pointsize=40)
p3 = plot(R,rgbcolor=(1,0,0),pointsize=40)
p4 = plot(Rneg,rgbcolor=(1,0,0),pointsize=40)
textp1 = point_txt(P,"$P$",rgbcolor=(0,0,0))
textp2 = point_txt(Q,"$Q$",rgbcolor=(0,0,0))
textp3 = point_txt(R,"$P+Q$",rgbcolor=(0,0,0))
if Lines==0:
g=curve
elif Lines ==1:
g=curve+l1
elif Lines == 2:
g=curve+l1+l2
if marked_points:
g=g+p1+p2+p3+p4
if P != Q:
g=g+textp1+textp2+textp3
else:
g=g+textp1+textp3
g.axes_range(xmin=-5,xmax=5,ymin=-13,ymax=13)
show(g,axes = Axes)
def line_from_curve_points(E,P,Q,style='-',rgb=(1,0,0),length=25):
"""
P,Q two points on an elliptic curve.
Output is a graphic representation of the straight line intersecting with P,Q.
"""
# The function tangent to P=Q on E
if P == Q:
if P[2]==0:
return line([(1,-length),(1,length)],linestyle=style,rgbcolor=rgb)
else:
# Compute slope of the curve E in P
l=-(3*P[0]^2 + 2*E.a2()*P[0] + E.a4() - E.a1()*P[1])/((-2)*P[1] - E.a1()*P[0] - E.a3())
f(x) = l * (x - P[0]) + P[1]
return plot(f(x),-length,length,linestyle=style,rgbcolor=rgb)
# Trivial case of P != R where P=O or R=O then we get the vertical line from the other point
elif P[2] == 0:
return line([(Q[0],-length),(Q[0],length)],linestyle=style,rgbcolor=rgb)
elif Q[2] == 0:
return line([(P[0],-length),(P[0],length)],linestyle=style,rgbcolor=rgb)
# Non trivial case where P != R
else:
# Case where x_1 = x_2 return vertical line evaluated in Q
if P[0] == Q[0]:
return line([(P[0],-length),(P[0],length)],linestyle=style,rgbcolor=rgb)
#Case where x_1 != x_2 return line trough P,R evaluated in Q"
l=(Q[1]-P[1])/(Q[0]-P[0])
f(x) = l * (x - P[0]) + P[1]
return plot(f(x),-length,length,linestyle=style,rgbcolor=rgb)