Differences between revisions 55 and 62 (spanning 7 versions)
⇤ ← Revision 55 as of 2014-12-23 02:05:59 →
Size: 45948
Editor: akhi
Comment:
← Revision 62 as of 2016-05-09 09:56:04 → ⇥
Size: 48431
Editor: akhi
Comment:
Deletions are marked like this. Additions are marked like this.
Line 872: Line 872:
= Multiple Zeta Values = = Multiple Zeta Values  =
Line 874: Line 874:
== Computing Multiple Zeta values == == Computing Multiple Zeta values (Euler-Zagier numbers) ==
Line 879: Line 879:
def _( weight=(5,(2..20))): def _( weight=(5,(2..100))):
Line 932: Line 932:
  print zeta(a)   u=zeta(a)
  RIF=RealIntervalField(int(3.321928*D))
  u=u/1
  print u
Line 939: Line 942:
def _( Depth=(5,(2..20))): def _( Depth=(5,(2..100))):
Line 998: Line 1001:

  print zeta(a)		   u=zeta(a)
  RIF=RealIntervalField(int(3.321928*D))
  u=u/1
  print u
Line 1002: Line 1007:
== Program to Compute Integer Relation between Multiple Zeta Values (Euler-Zagier numbers) ==
{{{#!sagecell
from mpmath import *
print "Enter the number of composition"
@interact
def _( n=(5,(2..100))):
 a=[]
 for i in range(n):
        a.append([i+2,1])
 print "In each box Enter composition as an array"
 @interact
 def _(v=('Compositions', input_box( default=a, to_value=lambda x: vector(flatten(x)))), accuracy=(100..100000)):
  D=accuracy
  R=RealField(10)
  a=v
  def comptobin(a):
        word=[]
        for i in range(len(a)):
                word=word+[0]*(a[i]-1)+[1]
        return(word)
  DD=int(D)+int(R(log(3.321928*D))/R(log(10)))+4
  RIF=RealIntervalField(DD)
  mp.dps=DD
  def Li(word):
        n=int(DD*log(10)/log(2))+1
        B=[]
        L=[]
        S=[]
        count=-1
        k=len(word)
        for i in range(k):
                B.append(mpf('0'))
                L.append(mpf('0'))
                if(word[i]==1 and i<k-1):
                        S.append(mpf('0'))
                        count=count+1
        T=mpf('1')
        for m in range(n):
                T=T/2
                B[k-1]=mpf('1')/(m+1)
                j=count
                for i in range(k-2,-1,-1):
                        if(word[i]==0):
                                B[i]=B[i+1]/(m+1)
                        elif(word[i]==1):
                                B[i]=S[j]/(m+1)
                                S[j]=S[j]+B[i+1]
                                j=j-1
                        L[i]=T*B[i]+L[i]
                L[k-1]=T*B[k-1]+L[k-1]
        return(L)
  def dual(a):
        b=list()
        b=a
        b=b[::-1]
        for i in range(len(b)):
                b[i]=1-b[i]
        return(b)
  def zeta(a):
        b=dual(a)
        l1=Li(a)+[1]
        l2=Li(b)+[1]
        Z=mpf('0')
        for i in range(len(l1)):
                Z=Z+l1[i]*l2[len(a)-i]
        return(Z)
  zet=[]
  for i in range(n):
        zet.append((zeta(comptobin(a[i]))))
  mp.dps=D
  for i in range(n):
        zet[i]=zet[i]/1
        print "zeta(",a[i],")=",zet[i]
  u=pslq(zet,tol=10**-D,maxcoeff=100,maxsteps=10000)
  print "the Intger Relation between the above zeta values given by the vector"
  print u
}}}
{{attachment:akhi10.png}}
Line 1006: Line 1088:
def _( weight=(7,(2..30))): def _( weight=(7,(2..100))):
Line 1030: Line 1112:
def _( Depth=(7,(1..30))): def _( Depth=(7,(1..100))):
Line 1051: Line 1133:
def _( weight=(7,(2..30))): def _( weight=(7,(2..100))):
Line 1075: Line 1157:
def _( w1=(2,(2..20)), w2=(2,(2..20))): def _( w1=(2,(2..100)), w2=(2,(2..100))):
Line 1162: Line 1244:
def _( w=(2,(2..20))): def _( w=(2,(2..100))):

Contents

  1. Integer Factorization
    1. Divisibility Poset
    2. Factor Trees
    3. Factoring an Integer
  2. Prime Numbers
    1. Illustrating the prime number theorem
    2. Prime Spiral - Square FIXME
    3. Prime Spiral - Polar
  3. Modular Forms
    1. Computing modular forms
    2. Computing the cuspidal subgroup
    3. A Charpoly and Hecke Operator Graph
  4. Modular Arithmetic
    1. Quadratic Residue Table FIXME
    2. Cubic Residue Table FIXME
  5. Cyclotomic Fields
    1. Gauss and Jacobi Sums in Complex Plane
    2. Exhaustive Jacobi Plotter
  6. Elliptic Curves
    1. Adding points on an elliptic curve
    2. Plotting an elliptic curve over a finite field
  7. Cryptography
    1. The Diffie-Hellman Key Exchange Protocol
  8. Other
    1. Continued Fraction Plotter
    2. Computing Generalized Bernoulli Numbers
    3. Fundamental Domains of SL_2(ZZ)
  9. Multiple Zeta Values
    1. Computing Multiple Zeta values (Euler-Zagier numbers)
      1. Word Input
      2. Composition Input
    2. Program to Compute Integer Relation between Multiple Zeta Values (Euler-Zagier numbers)
    3. Word to composition
    4. Composition to Word
    5. Dual of a Word
    6. Shuffle product of two Words
    7. Shuffle Regularization at 0
    8. Shuffle Regularization at 1

Integer Factorization

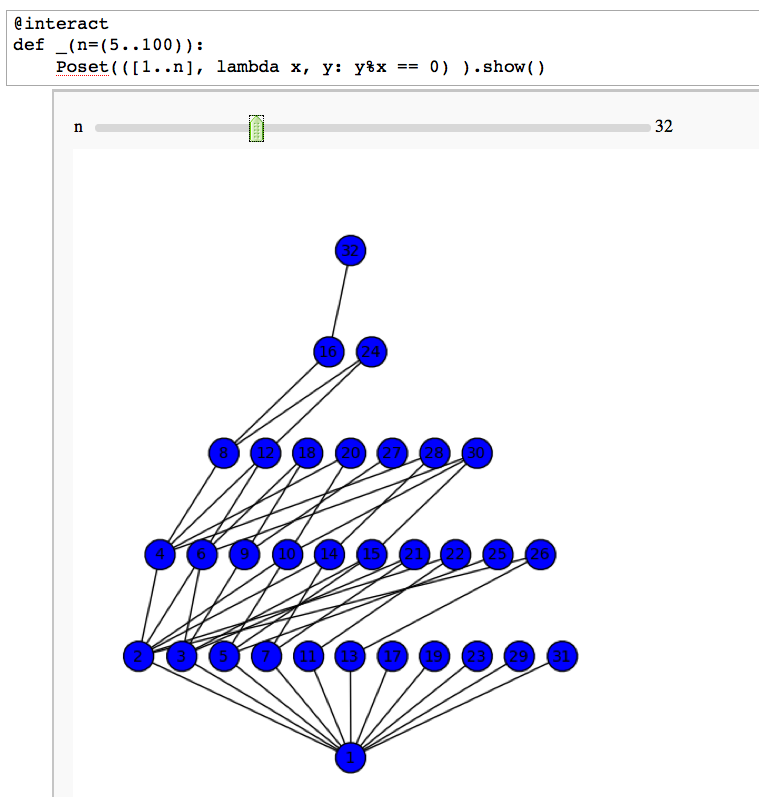
Divisibility Poset

by William Stein

divposet.png

Factor Trees

by William Stein

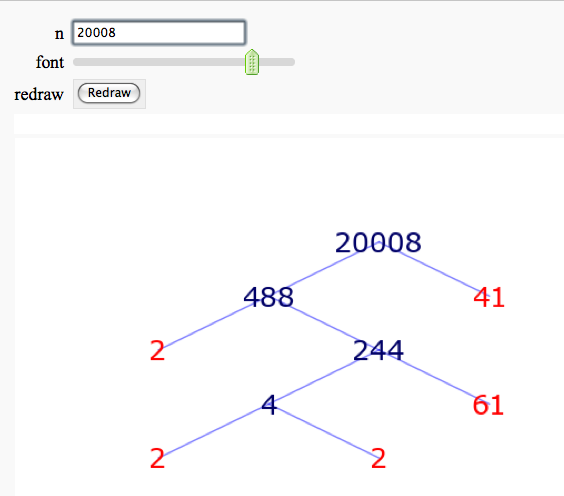
factortree.png

More complicated demonstration using Mathematica: http://demonstrations.wolfram.com/FactorTrees/

Factoring an Integer

by Timothy Clemans

Sage implementation of the Mathematica demonstration of the same name. http://demonstrations.wolfram.com/FactoringAnInteger/

Prime Numbers

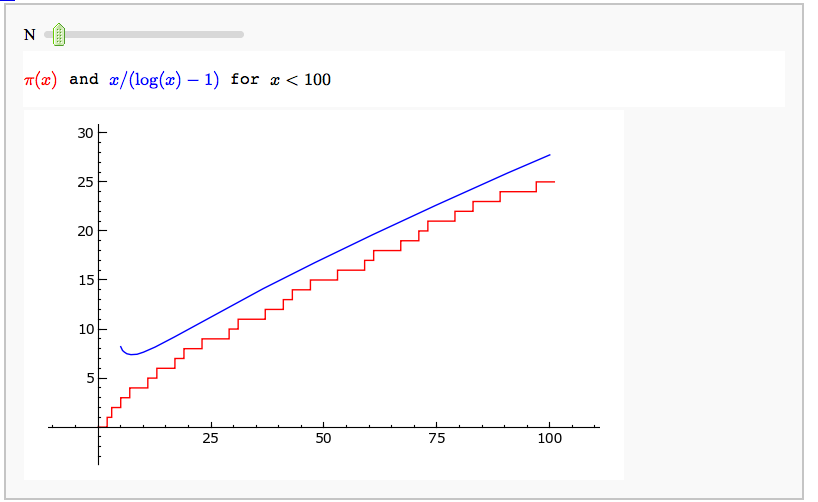
Illustrating the prime number theorem

by William Stein

primes.png

Prime Spiral - Square FIXME

by David Runde

SquareSpiral.PNG

Prime Spiral - Polar

by David Runde

PolarSpiral.PNG

Modular Forms

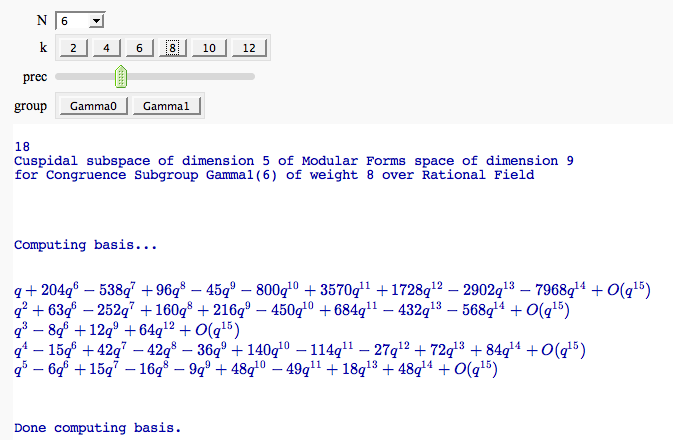
Computing modular forms

by William Stein

modformbasis.png

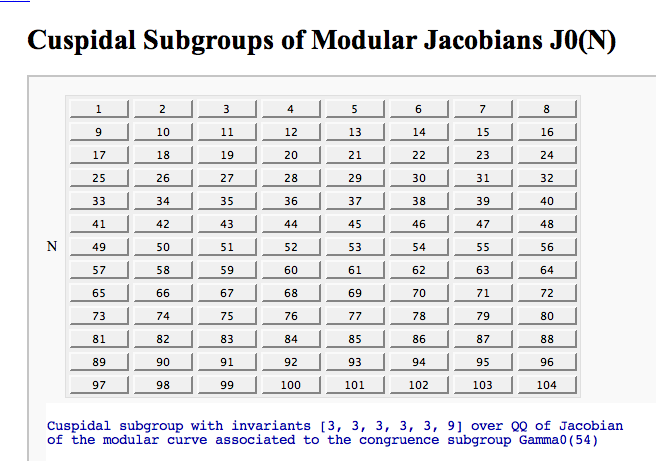
Computing the cuspidal subgroup

by William Stein

cuspgroup.png

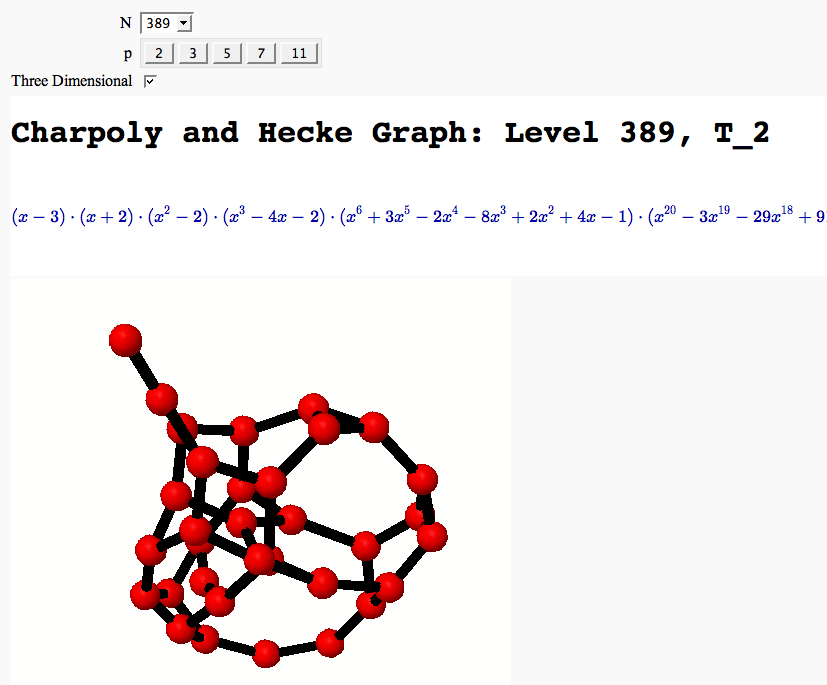
A Charpoly and Hecke Operator Graph

by William Stein

heckegraph.png

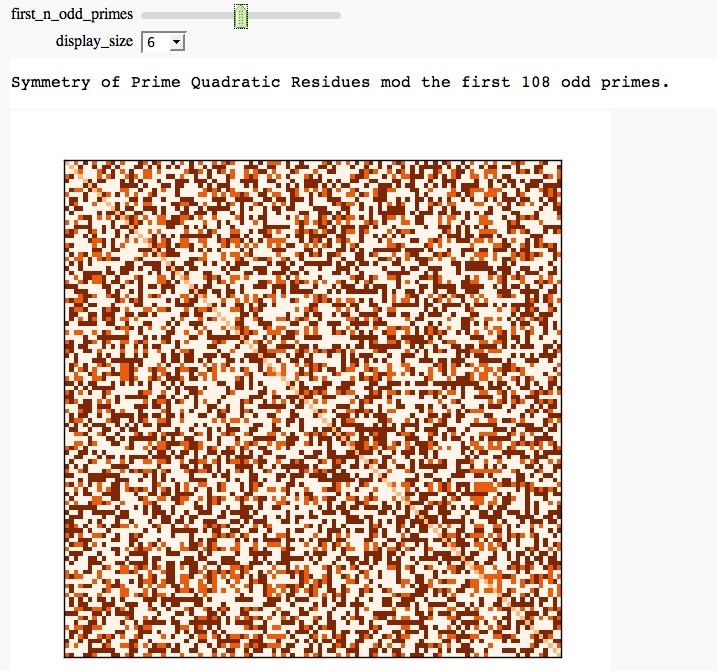
Modular Arithmetic

Quadratic Residue Table FIXME

by Emily Kirkman

quadres.png

quadresbig.png

Cubic Residue Table FIXME

by Emily Kirkman

cubres.png

Cyclotomic Fields

Gauss and Jacobi Sums in Complex Plane

by Emily Kirkman

jacobising.png

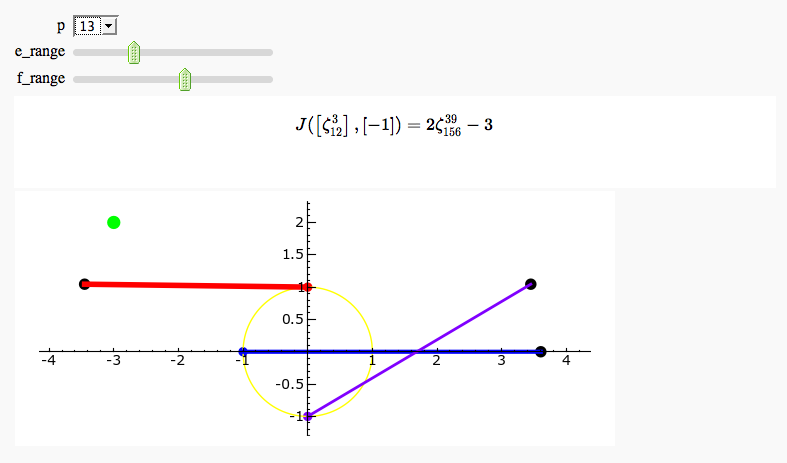
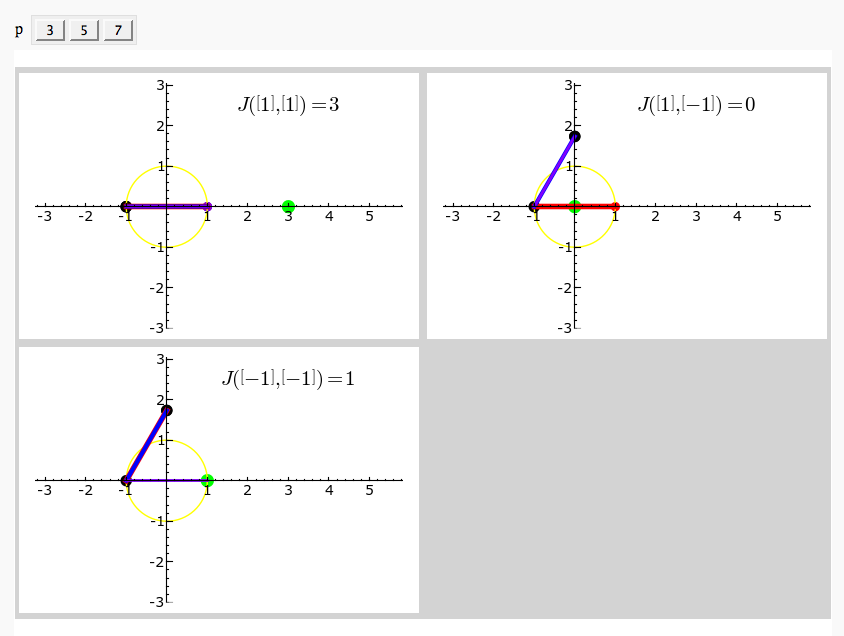
Exhaustive Jacobi Plotter

by Emily Kirkman

jacobiexh.png

Elliptic Curves

Adding points on an elliptic curve

by David Møller Hansen

PointAddEllipticCurve.png

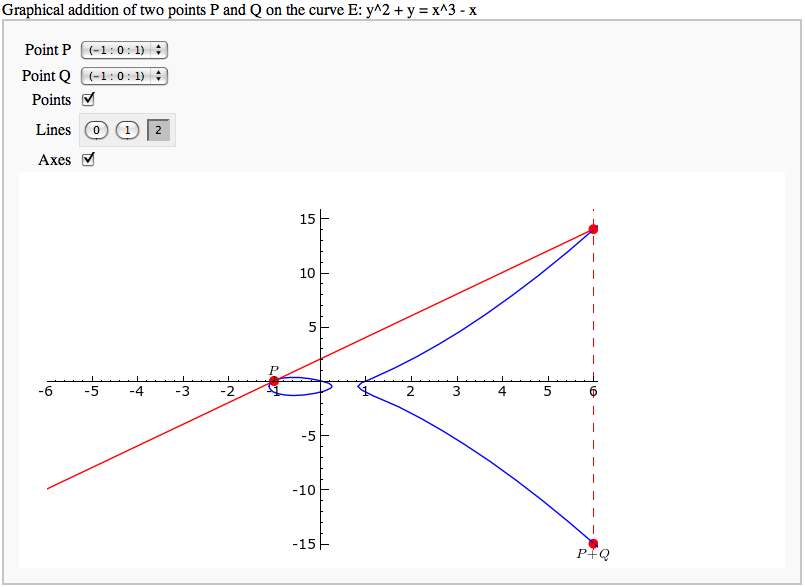
Plotting an elliptic curve over a finite field

ellffplot.png

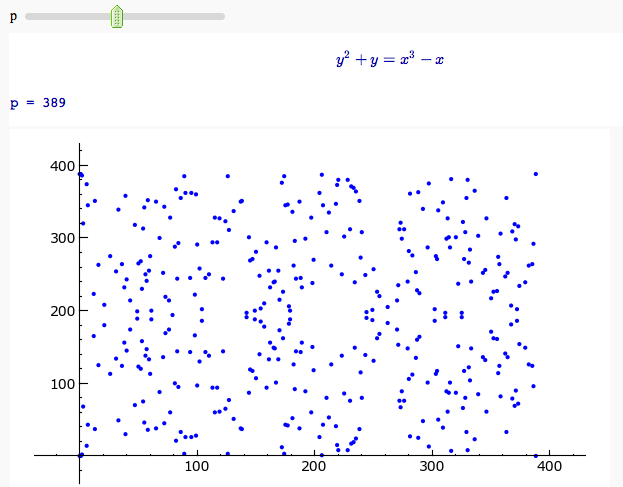
Cryptography

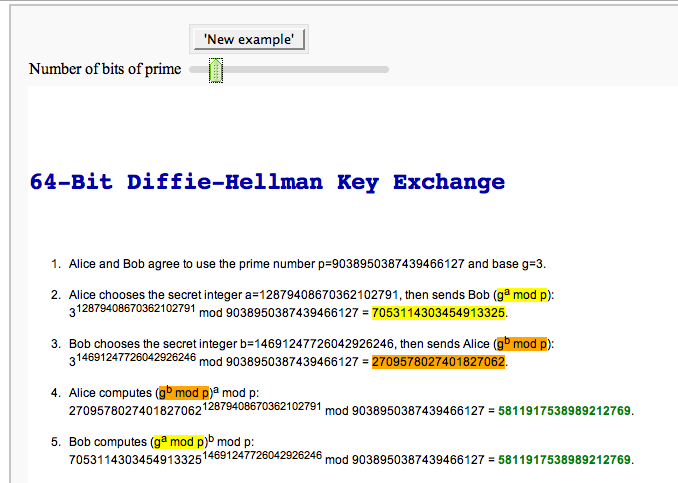
The Diffie-Hellman Key Exchange Protocol

by Timothy Clemans and William Stein

dh.png

Other

Continued Fraction Plotter

by William Stein

contfracplot.png

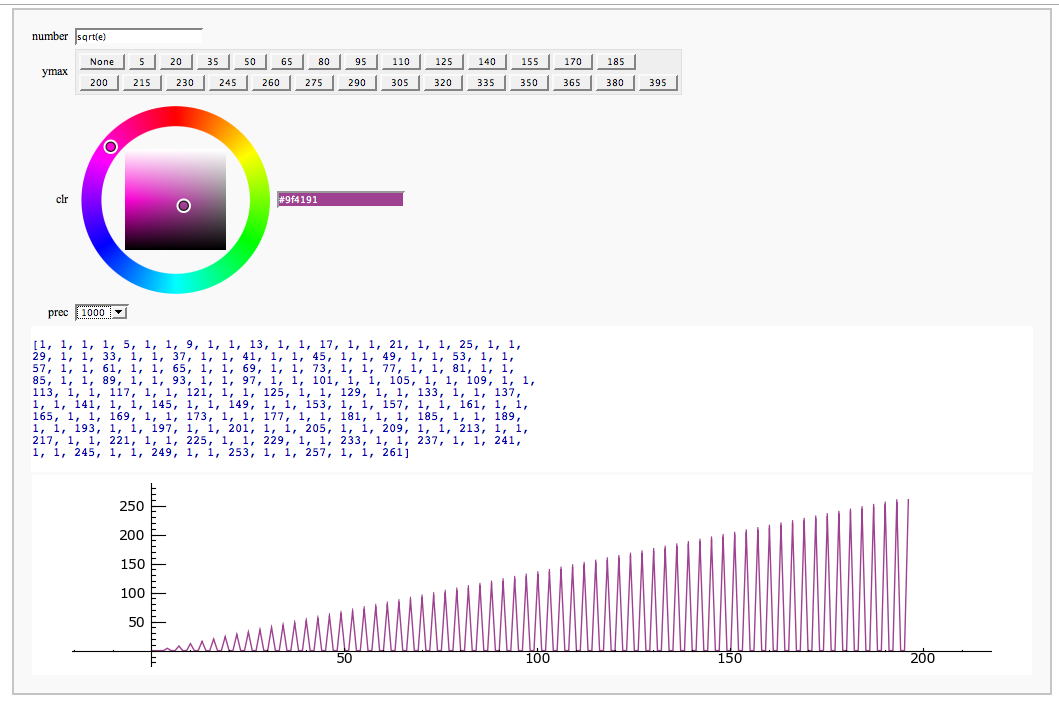
Computing Generalized Bernoulli Numbers

by William Stein (Sage-2.10.3)

bernoulli.png

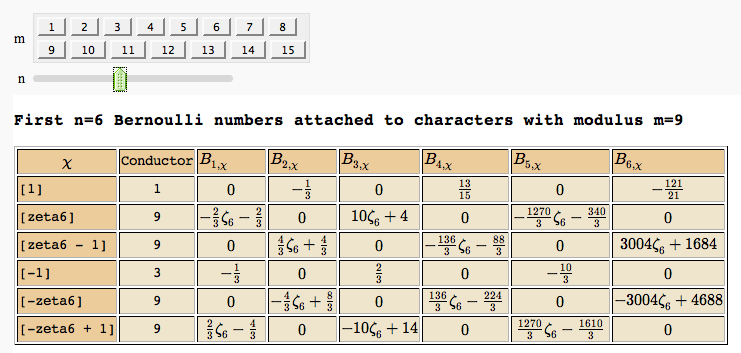
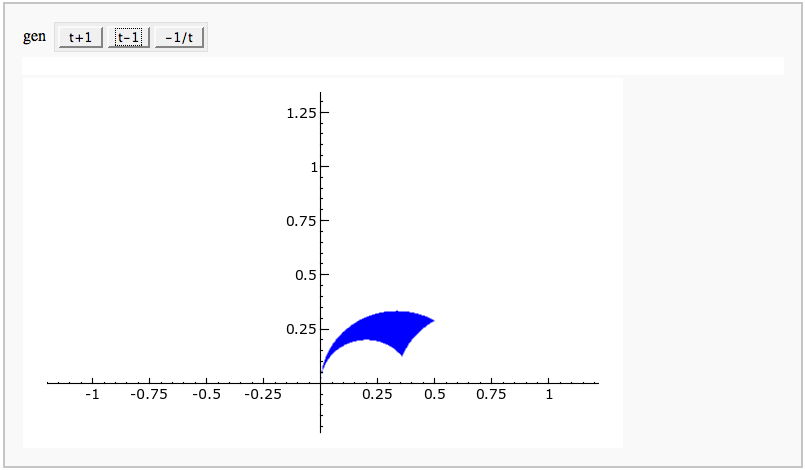
Fundamental Domains of SL_2(ZZ)

by Robert Miller

fund_domain.png

Multiple Zeta Values

by Akhilesh P.

Computing Multiple Zeta values (Euler-Zagier numbers)

Word Input

akhi1.png

Composition Input

akhi5.png

Program to Compute Integer Relation between Multiple Zeta Values (Euler-Zagier numbers)

akhi10.png

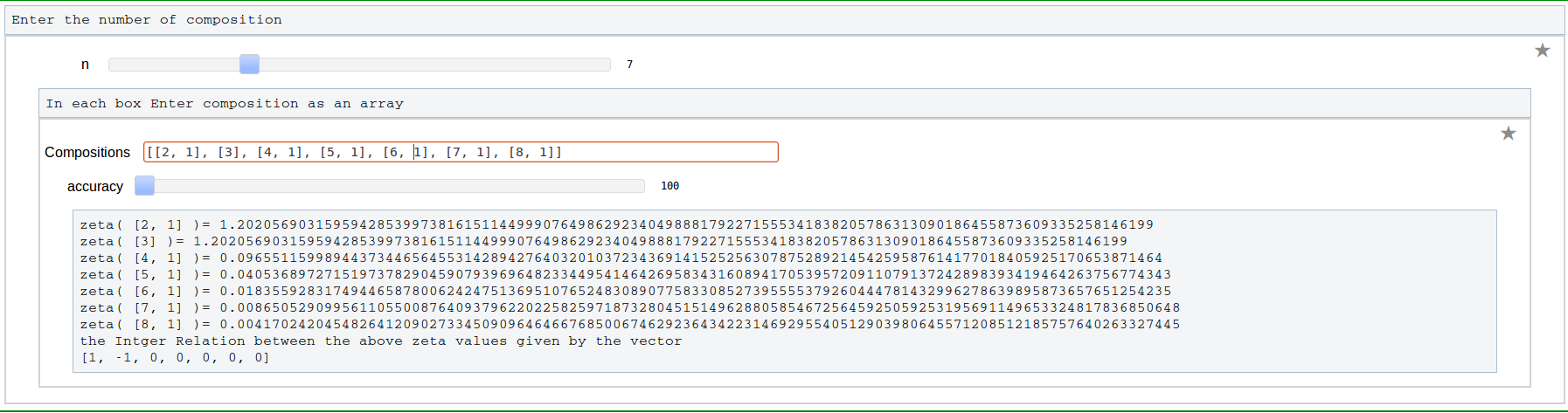
Word to composition

akhi2.png

Composition to Word

akhi3.png

Dual of a Word

akhi4.png

Shuffle product of two Words

akhi6.png

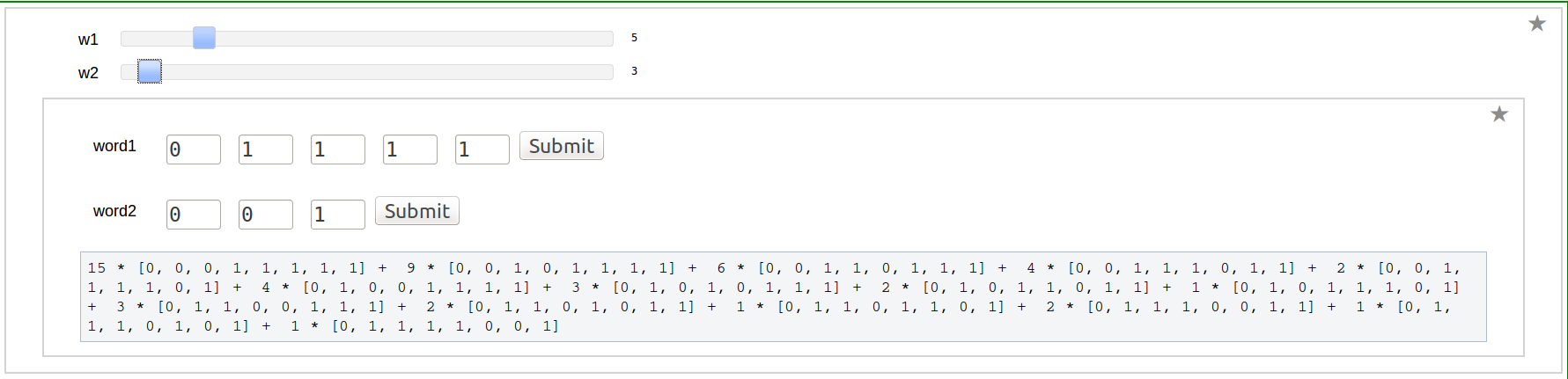
Shuffle Regularization at 0

akhi7.png

Shuffle Regularization at 1

akhi8.png

interact/number_theory (last edited 2020-06-14 09:10:48 by chapoton)