|
⇤ ← Revision 1 as of 2011-03-15 14:45:31
Size: 2366
Comment: Started section with "Winding number of a plane curve"
|
Size: 2457
Comment: detail: show the origin
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 7: | Line 7: |
| by Pablo Angulo. Computes winding number as an integral, and also as a intersection number with a half line through the origin. | by Pablo Angulo. Computes winding number (with respect to the origin!) as an integral, and also as a intersection number with a half line through the origin. |
| Line 73: | Line 73: |
| arrow((x(0),y(0)), (x(0) + xp1(0), y(0) + yp1(0))) ) | arrow((x(0),y(0)), (x(0) + xp1(0), y(0) + yp1(0))) + point2d([(0,0)], color = 'black', pointsize = 70)) |
Sage Interactions - Topology
goto interact main page
Winding number of a plane curve
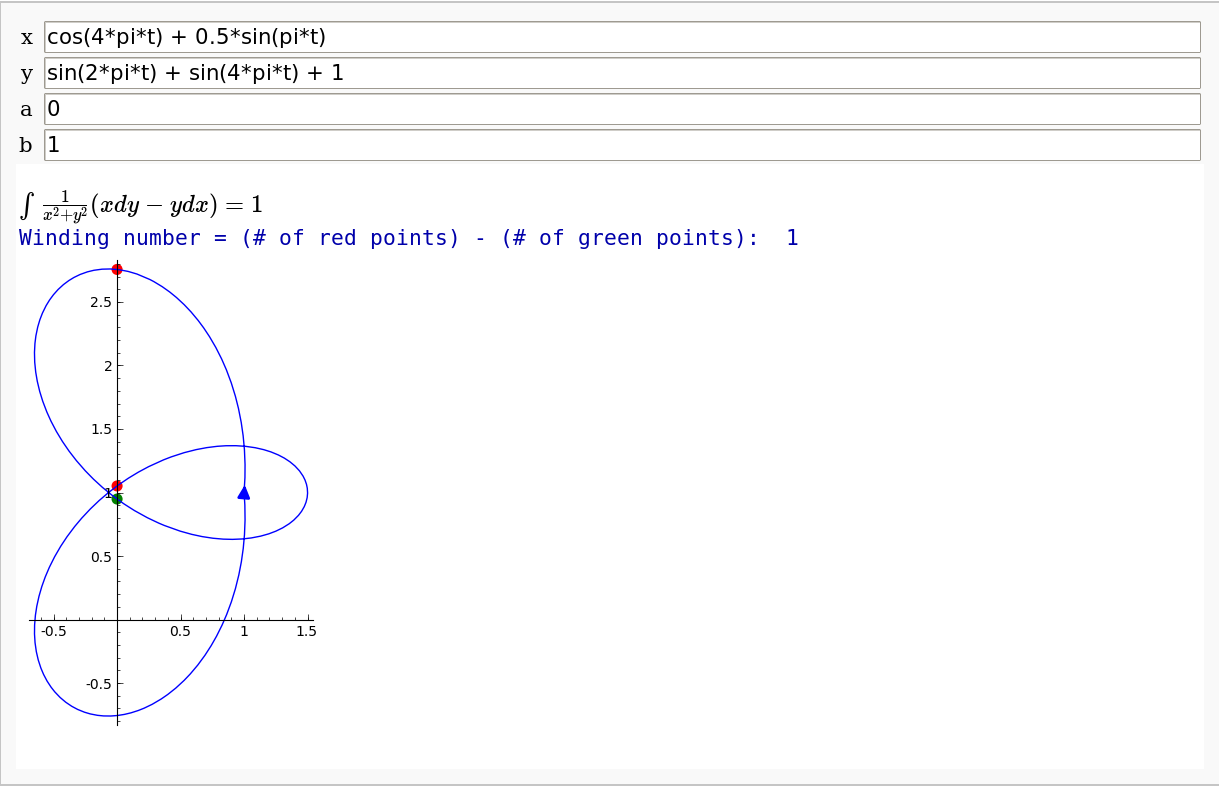
by Pablo Angulo. Computes winding number (with respect to the origin!) as an integral, and also as a intersection number with a half line through the origin.
var('t')
def winding_number_integral(x, y, a, b):
r2 = x^2 + y^2
xp = x.derivative(t)
yp = y.derivative(t)
integrando = (x*yp -y*xp)/r2
i,e = numerical_integral(integrando, a, b)
return round(i/(2*pi))
N = 20
epsilon = 1e-7
def all_the_zeros(f, a, b):
'''all_the_zeros de f(t), asuming f is periodic'''
delta= (b-a)/N
zeros = []
for t in srange(a, b ,delta):
try:
zeros.append(find_root(f, t-epsilon, t+delta+epsilon))
except:
pass
zeros.sort()
if not zeros: return zeros
if abs(zeros[0] + 2*pi - zeros[-1])<epsilon:
zeros.pop()
zeros_cleaned = [zeros.pop(0)]
for c in zeros:
if abs(c - zeros_cleaned[-1])>epsilon:
zeros_cleaned.append(c)
if abs(zeros[0] + 2*pi - zeros[-1])<epsilon:
zeros.pop()
return zeros_cleaned
@interact
def _(x = cos(4*pi*t), y = 1 + sin(2*pi*t) + sin(4*pi*t),
a = 0, b = 1):
x = x.function(t); y = y.function(t);
if abs(x(a)-x(b)) + abs(y(a)-y(b)) > epsilon:
raise ValueError, "Curve is not closed!"
xp = x.derivative(t)
yp = y.derivative(t)
xp1 = xp/(xp^2 + yp^2)
yp1 = yp/(xp^2 + yp^2)
html(r'$\int \frac{1}{x^2 + y^2}(xdy-ydx)=%d$'%winding_number_integral(x,y,a,b))
zeros = all_the_zeros(x,a, b)
wn = 0
left2right = []
right2left = []
for t0 in zeros:
if y(t0)>0:
if xp(t0) > 0:
left2right.append((x(t0), y(t0)))
wn -= 1
else:
right2left.append((x(t0), y(t0)))
wn += 1
print 'Winding number = (# of red points) - (# of green points): ', wn
p = (parametric_plot((x,y),(t,0,1)) +
arrow((x(0),y(0)), (x(0) + xp1(0), y(0) + yp1(0))) +
point2d([(0,0)], color = 'black', pointsize = 70))
if left2right:
p += point2d(left2right , color = 'green', pointsize = 50)
if right2left:
p += point2d(right2left , color = 'red', pointsize = 50)
p.show(aspect_ratio=1)