|
Size: 7572
Comment:
|
Size: 2619
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 3: | Line 3: |
| Post code that demonstrates the use of the interact command in Sage here. It should be easy for people to just scroll through and paste examples out of here into their own sage notebooks. | This is a collection of pages demonstrating the use of the **interact** command in Sage. It should be easy to just scroll through and copy/paste examples into Sage notebooks. If you have suggestions on how to improve interact, add them [[interact/Suggestions|here]] or email the sage-support mailing list. Of course, your own examples are also welcome! |
| Line 5: | Line 8: |
| We'll likely restructure and reorganize this once we have some nontrivial content and get a sense of how it is laid out. | Documentation links: |
| Line 7: | Line 10: |
| == Graph Theory == | * [[http://doc.sagemath.org/html/en/reference/repl/sage/repl/ipython_kernel/interact.html| interacts in the Jupyter notebook]] (see this page and the two following ones) * [[https://github.com/sagemath/sagenb/blob/master/sagenb/notebook/interact.py|interacts in the legacy SageNB notebook]] (many helpful examples) * [[https://github.com/sagemath/sagecell/blob/master/interact_compatibility.py|Sage Cell Server implementation]] * [[https://github.com/sagemathinc/cocalc/blob/master/src/smc_sagews/smc_sagews/sage_salvus.py#L348|CoCalc Sage worksheet implementation]] |
| Line 9: | Line 15: |
| === Automorphism Groups of some Graphs === | Examples: |
| Line 11: | Line 17: |
| by William Stein (I spent less than five minutes on this): | * [[interact/algebra|Algebra]] * [[interact/bio|Bioinformatics]] * [[interact/calculus|Calculus]] * [[interact/cryptography|Cryptography]] * [[interact/diffeq|Differential Equations]] * [[interact/graphics|Drawing Graphics]] * [[interact/dynsys|Dynamical Systems]] * [[interact/fractal|Fractals]] * [[interact/games|Games and Diversions]] * [[interact/geometry|Geometry]] * [[interact/graph_theory|Graph Theory]] * [[interact/linear_algebra|Linear Algebra]] * [[interact/Loop Quantum Gravity|Loop Quantum Gravity]] * [[interact/misc|Miscellaneous]] * [[interact/number_theory|Number Theory]] * [[interact/stats|Statistics/Probability]] * [[interact/topology|Topology]] * [[interact/web|Web Applications]] |
| Line 13: | Line 36: |
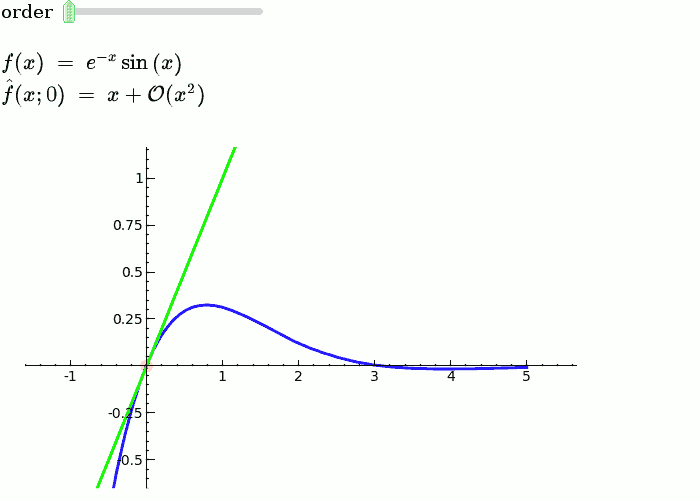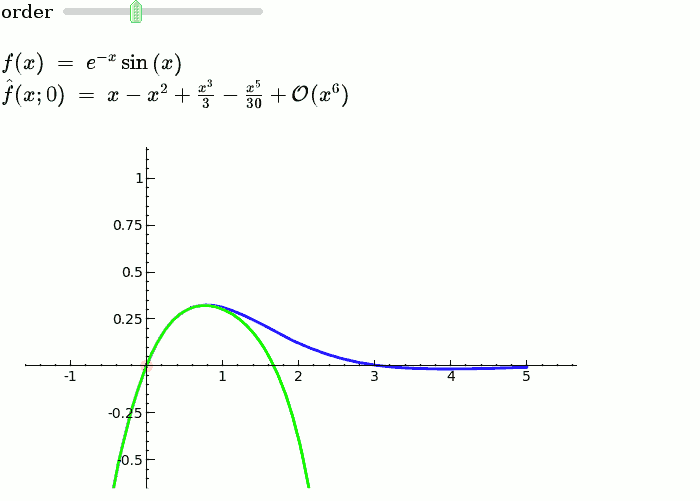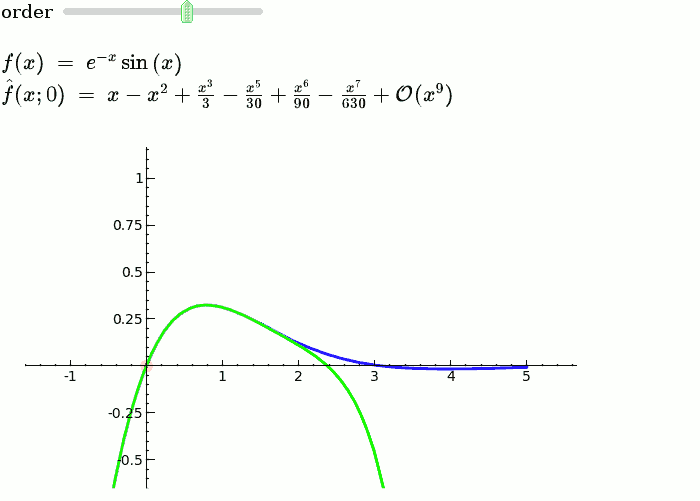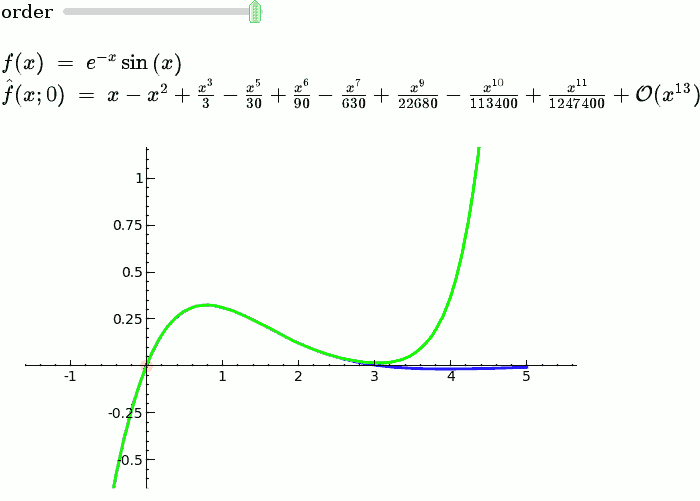
| {{{ | == Explanatory example: Taylor Series == This is the code and a mockup animation of the interact command. It defines a slider, seen on top, that can be dragged. Once dragged, it changes the value of the variable "order" and the whole block of code gets evaluated. This principle can be seen in various examples presented on the pages above! {{{#!sagecell x = SR.var('x') x0 = 0 f = sin(x) * e^(-x) p = plot(f, -1, 5, thickness=2) dot = point((x0, f(x=x0)), pointsize=80, rgbcolor=(1, 0, 0)) |
| Line 15: | Line 48: |
| def _(graph=['CycleGraph', 'CubeGraph', 'RandomGNP'], n=selector([1..10],nrows=1), p=selector([10,20,..,100],nrows=1)): print graph if graph == 'CycleGraph': print "n (=%s): number of vertices"%n G = graphs.CycleGraph(n) elif graph == 'CubeGraph': if n > 8: print "n reduced to 8" n = 8 print "n (=%s): dimension"%n G = graphs.CubeGraph(n) elif graph == 'RandomGNP': print "n (=%s) vertices"%n print "p (=%s%%) probability"%p G = graphs.RandomGNP(n, p/100.0) print G.automorphism_group() show(plot(G)) |
def _(order=slider([1 .. 12])): ft = f.taylor(x, x0, order) pt = plot(ft, -1, 5, color='green', thickness=2) pretty_print(html(r'$f(x)\;=\;%s$' % latex(f))) pretty_print(html(r'$\hat{f}(x;%s)\;=\;%s+\mathcal{O}(x^{%s})$' % (x0, latex(ft), order+1))) show(dot + p + pt, ymin=-.5, ymax=1) |
| Line 35: | Line 55: |
== Calculus == === A contour map and 3d plot of two inverse distance functions === by William Stein {{{ @interact def _(q1=(-1,(-3,3)), q2=(-2,(-3,3)), cmap=['autumn', 'bone', 'cool', 'copper', 'gray', 'hot', 'hsv', 'jet', 'pink', 'prism', 'spring', 'summer', 'winter']): x,y = var('x,y') f = q1/sqrt((x+1)^2 + y^2) + q2/sqrt((x-1)^2+(y+0.5)^2) C = contour_plot(f, (-2,2), (-2,2), plot_points=30, contours=15, cmap=cmap) show(C, figsize=3, aspect_ratio=1) show(plot3d(f, (x,-2,2), (y,-2,2)), figsize=5, viewer='tachyon') }}} attachment:mountains.png == Linear Algebra == === Numerical instability of the classical Gram-Schmidt algorithm === by Marshall Hampton (tested by William Stein, who thinks this is really nice!) {{{ def GS_classic(a_list): ''' Given a list of vectors or a matrix, returns the QR factorization using the classical (and numerically unstable) Gram-Schmidt algorithm. ''' if type(a_list) != list: cols = a_list.cols() a_list = [x for x in cols] indices = range(len(a_list)) q = [] r = [[0 for i in indices] for j in indices] v = [a_list[i].copy() for i in indices] for i in indices: for j in range(0,i): r[j][i] = q[j].inner_product(a_list[i]) v[i] = v[i] - r[j][i]*q[j] r[i][i] = (v[i]*v[i])^(1/2) q.append(v[i]/r[i][i]) q = matrix([q[i] for i in indices]).transpose() return q, matrix(r) def GS_modern(a_list): ''' Given a list of vectors or a matrix, returns the QR factorization using the 'modern' Gram-Schmidt algorithm. ''' if type(a_list) != list: cols = a_list.cols() a_list = [x for x in cols] indices = range(len(a_list)) q = [] r = [[0 for i in indices] for j in indices] v = [a_list[i].copy() for i in indices] for i in indices: r[i][i] = v[i].norm(2) q.append(v[i]/r[i][i]) for j in range(i+1, len(indices)): r[i][j] = q[i].inner_product(v[j]) v[j] = v[j] - r[i][j]*q[i] q = matrix([q[i] for i in indices]).transpose() return q, matrix(r) html('<h2>Numerical instability of the classical Gram-Schmidt algorithm</h2>') @interact def gstest(precision = slider(range(3,53), default = 10), a1 = input_box([1,1/1000,1/1000]), a2 = input_box([1,1/1000,0]), a3 = input_box([1,0,1/1000])): myR = RealField(precision) displayR = RealField(5) html('precision in bits: ' + str(precision) + '<br>') A = matrix([a1,a2,a3]) A = [vector(myR,x) for x in A] qn, rn = GS_classic(A) qb, rb = GS_modern(A) html('Classical Gram-Schmidt:') show(matrix(displayR,qn)) html('Stable Gram-Schmidt:') show(matrix(displayR,qb)) }}} attachment:GramSchmidt.png == Number Theory == === Illustrating the prime number thoerem === by William Stein {{{ @interact def _(N=(100,(2..2000))): html("<font color='red'>$\pi(x)$</font> and <font color='blue'>$x/(\log(x)-1)$</font> for $x < %s$"%N) show(plot(prime_pi, 0, N, rgbcolor='red') + plot(x/(log(x)-1), 5, N, rgbcolor='blue')) }}} attachment:primes.png === Computing the cuspidal subgroup === by William Stein {{{ html('<h1>Cuspidal Subgroups of Modular Jacobians J0(N)</h1>') @interact def _(N=selector([1..8*13], ncols=8, width=10, default=10)): A = J0(N) print A.cuspidal_subgroup() }}} attachment:cuspgroup.png === A Charpoly and Hecke Operator Graph === by William Stein {{{ # Note -- in Sage-2.10.3; multiedges are missing in plots; loops are missing in 3d plots @interact def f(N = prime_range(11,400), p = selector(prime_range(2,12),nrows=1), three_d = ("Three Dimensional", False)): S = SupersingularModule(N) T = S.hecke_matrix(p) G = Graph(T, multiedges=True, loops=not three_d) html("<h1>Charpoly and Hecke Graph: Level %s, T_%s</h1>"%(N,p)) show(T.charpoly().factor()) if three_d: show(G.plot3d(), aspect_ratio=[1,1,1]) else: show(G.plot(),figsize=7) }}} attachment:heckegraph.png === Demonstrating the Diffie-Hellman Key Exchange Protocol === by Timothy Clemans (refereed by William Stein) {{{ @interact def diffie_hellman(button=selector(["New example"],label='',buttons=True), bits=("Number of bits of prime", (8,12,..512))): maxp = 2^bits p = random_prime(maxp) k = GF(p) g = k.multiplicative_generator() a = ZZ.random_element(10, maxp) b = ZZ.random_element(10, maxp) print """ <html> <style> .gamodp { background:yellow } .gbmodp { background:orange } .dhsame { color:green; font-weight:bold } </style> <h2>%s-Bit Diffie-Hellman Key Exchange</h2> <ol style="color:#000;font:12px Arial, Helvetica, sans-serif"> <li>Alice and Bob agree to use the prime number p=%s and base g=%s.</li> <li>Alice chooses the secret integer a=%s, then sends Bob (<span class="gamodp">g<sup>a</sup> mod p</span>):<br/>%s<sup>%s</sup> mod %s = <span class="gamodp">%s</span>.</li> <li>Bob chooses the secret integer b=%s, then sends Alice (<span class="gbmodp">g<sup>b</sup> mod p</span>):<br/>%s<sup>%s</sup> mod %s = <span class="gbmodp">%s</span>.</li> <li>Alice computes (<span class="gbmodp">g<sup>b</sup> mod p</span>)<sup>a</sup> mod p:<br/>%s<sup>%s</sup> mod %s = <span class="dhsame">%s</span>.</li> <li>Bob computes (<span class="gamodp">g<sup>a</sup> mod p</span>)<sup>b</sup> mod p:<br/>%s<sup>%s</sup> mod %s = <span class="dhsame">%s</span>.</li> </ol></html> """ % (bits, p, g, a, g, a, p, (g^a), b, g, b, p, (g^b), (g^b), a, p, (g^ b)^a, g^a, b, p, (g^a)^b) }}} attachment:dh.png === Somewhat Silly Egg Painter === by Marshall Hampton (refereed by William Stein) {{{ var('s,t') g(s) = ((0.57496*sqrt(121 - 16.0*s^2))/sqrt(10.+ s)) def P(color, rng): return parametric_plot3d((cos(t)*g(s), sin(t)*g(s), s), (s,rng[0],rng[1]), (t,0,2*pi), plot_points = [150,150], rgbcolor=color, frame = False, opacity = 1) colorlist = ['red','blue','red','blue'] @interact def _(band_number = selector(range(1,5)), current_color = Color('red')): html('<h1 align=center>Egg Painter</h1>') colorlist[band_number-1] = current_color egg = sum([P(colorlist[i],[-2.75+5.5*(i/4),-2.75+5.5*(i+1)/4]) for i in range(4)]) show(egg) }}} attachment:eggpaint.png |
{{attachment:taylor_series_animated.gif}} |
Sage Interactions
This is a collection of pages demonstrating the use of the **interact** command in Sage. It should be easy to just scroll through and copy/paste examples into Sage notebooks. If you have suggestions on how to improve interact, add them here or email the sage-support mailing list. Of course, your own examples are also welcome!
Documentation links:
interacts in the Jupyter notebook (see this page and the two following ones)
interacts in the legacy SageNB notebook (many helpful examples)
Examples:
Explanatory example: Taylor Series
This is the code and a mockup animation of the interact command. It defines a slider, seen on top, that can be dragged. Once dragged, it changes the value of the variable "order" and the whole block of code gets evaluated. This principle can be seen in various examples presented on the pages above!